Wyjaśnienie proporcjonalności kompozytowej, trzy złożone reguły, ćwiczenia

Złożona lub wielokrotność proporcjonalności Jest to związek między więcej niż dwoma wielkościami, w których można zaobserwować bezpośrednią i odwrotną proporcjonalność między danymi a nieznanymi. Jest to bardziej zaawansowana wersja prostej proporcjonalności, chociaż techniki stosowane w obu procedurach są podobne.

Na przykład, jeśli 7 osób jest potrzebnych do pobrania 10 ton towarów w ciągu 3 godzin, proporcjonalność złożona może być użyta do obliczenia, ile osób będzie potrzebnych do pobrania 15 ton w 4 godziny.

Źródło: Pixabay.com

Aby odpowiedzieć na to pytanie, wygodne jest stworzenie tabeli wartości, aby zbadać i powiązać wielkości i niewiadome.

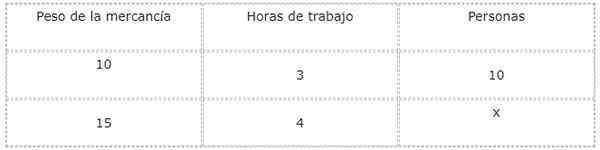
Analizowane są rodzaje relacji między każdą wielkością a obecną nieznaną, co w tym przypadku odpowiada liczbie osób, które będą pracować.

Wraz ze wzrostem wagi produktów liczba osób potrzebnych do pobrania również wzrasta. Z tego powodu związek między wagą a pracownikami jest bezpośredni.

Z drugiej strony, zwiększając liczbę pracowników, godziny pracy spada. Z tego powodu związek między ludźmi a godzinami pracy jest odwrotny.

[TOC]

Jak obliczyć proporcjonalność złożonych

Aby rozwiązać przykłady, takie jak poprzedni, najczęściej stosuje się metodę reguły złożonej. Polega to na ustaleniu rodzajów relacji między wielkościami i niewiadomymi, a następnie przedstawieniem produktu między ułamkami.

W odniesieniu do początkowego przykładu frakcje odpowiadające tabeli wartości są zorganizowane w następujący sposób:

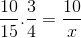
Ale przed rozwiązaniem i wyczyszczeniem nieznanych frakcje odpowiadające odwrotnej relacji należy odwrócić. Że w tym przypadku odpowiada zmiennej czasowej. W ten sposób operacja zostanie rozwiązana:

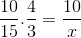
Której jedyną różnicą jest inwestycja ułamka odpowiadająca zmiennego czasu 4/3. Wartość x jest obsługiwana i jasna.

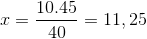
Zatem do pobrania 15 ton towarów potrzebnych jest więcej niż jedenastka osób.

Wyjaśnienie

Proporcjonalność to stały związek między wielkościami, które podlegają zmianom, które będą symetryczne dla każdej z zaangażowanych wielkości. Istnieją bezpośrednio i odwrotnie proporcjonalne związki, definiując w ten sposób parametry prostej lub złożonej proporcjonalności.

Bezpośrednio trzy zasady

Składa się ze stosunku proporcji między zmiennymi, które stanowią takie samo zachowanie po modyfikowaniu. Jest to bardzo częste w obliczaniu wartości procentowych związanych z różnymi wielkościami stu, gdzie doceniana jest jego podstawowa struktura.

Jako przykład można obliczyć 15% z 63. Na pierwszy rzut oka, wspomniany odsetek nie można zobaczyć w prosty sposób. Ale wdrażanie zasady trzech możesz dokonać następujący związek: jeśli 100% to 63, to 15%, ile to będzie?

Może ci służyć: Twierdzenie o czynniku: wyjaśnienie, przykłady, ćwiczenia

100%-63

15%-x

A odpowiednia operacja to:

(piętnaście% . 63) / 100% = 9,45

Gdzie uproszczone są znaki procentowe i osiągnięto 9,45 figury, która stanowi 15% z 63.

Trzy reguły odwrotne

Jak sama nazwa wskazuje, w tym przypadku związek między zmiennymi jest przeciwny. Odwrotne relacje należy ustalić przed przejściem do obliczeń. Jego procedura jest homologiczna dla trzech bezpośrednich zasad, z wyjątkiem inwestycji w ułamek, który ma zostać obliczona.

Na przykład 3 malarze potrzebują 5 godzin, aby wykończyć ścianę. Ile godzin skończyłyby 4 malarzy?

W tym przypadku związek jest odwrotny, ponieważ poprzez zwiększenie liczby malarzy czas pracy powinien skrócić. Związek jest ustanowiony;

3 malarzy - 5 godzin

4 malarzy- x godziny

Gdy związek jest odwrotny, kolejność operacji jest odwrócona. To jest właściwy sposób;

(3 malarzy) . (5 godzin) / 4 malarzy = 3,75 godziny

Termin malarze jest uproszczony, a wynik wynosi 3,75 godziny.

Stan

Być w obecności związku lub wielu proporcjonalności, konieczne jest znalezienie obu rodzajów zależności między wielkościami i zmiennymi.

- Direct: zmienna przedstawia to samo zachowanie co nieznane. To znaczy, zwiększając lub zmniejszając jedno, drugi jest zmieniony równo.

- Odwrotne: zmienna przedstawia zachowanie antonimiczne nieznane. Ułamek, który określa tę zmienną w tabeli wartości, musi zostać odwrócona, aby przedstawić odwrotnie proporcjonalną zależność między zmienną a nieznaną.

Weryfikacja wyników

Bardzo często zdezorientowanie kolejności wielkości podczas pracy z proporcjonalnością złożoną, w przeciwieństwie do tego, co dzieje się w zwykłych obliczeniach proporcji, których natura jest w większości bezpośrednia i postojenna za pomocą prostej trzech zasad.

Dlatego ważne jest zbadanie logicznej kolejności wyników, weryfikując spójność liczb rzucanych przez trzy złożone zasady.

W początkowym przykładzie popełnienie tego błędu oznaczałoby uzyskanie 20 w rezultacie. To znaczy 20 osób do pobrania 15 ton towarów w ciągu 4 godzin.

Na pierwszy rzut oka nie wydaje się to szalonym rezultatem, ale wzrost prawie 200% w personelu (z 7 do 20 osób) jest ciekawy, gdy wzrost towarów wynosi 50%, a nawet z większym marginesem czasu na wykonanie praca.

Może ci służyć: ogólne równanie paraboli (przykłady i ćwiczenia)

W ten sposób logiczna weryfikacja wyników stanowi ważny krok poprzez wdrożenie trzech złożonych reguły.

Luz

Chociaż o bardziej podstawowym charakterze w zakresie tworzenia matematycznego, zezwolenie stanowi ważny krok w przypadkach proporcjonalności. Błędny klirens jest wystarczający do unieważnienia dowolnego wyniku uzyskanego w kolejności trzech prostych lub złożonych.

Historia

Reguła trzech stała się znana na Zachodzie przez Arabów, z publikacjami kilku autorów. Wśród nich al-Jwarizmi i al-Biruni.

Al-Biruni, dzięki swojej wiedzy wielokulturowej, miał dostęp do ogromnych informacji dotyczących tej praktyki podczas podróży do Indii, będąc odpowiedzialnym za najszerszą dokumentację o trzech zasadach trzech.

W jego śledztwie powstaje, że Indie były pierwszym miejscem, w którym użycie trzech zasad zostało powszechne. Pisarz zapewnia, że ​​został on płynnie wykonany w jego bezpośrednich, odwrotnych, a nawet skomponowanych wersjach.

Dokładna data, w której trzy zasady stały się częścią wiedzy matematycznej Indii, jest nadal nieznana. Jednak najstarszy dokument skierowany do tej praktyki, rękopis Bakhshali, został odkryty w 1881 roku. Obecnie jest w Oksfordzie.

Wielu historyków matematyki zapewnia, że ​​ten manuskrypt pochodzi z początku obecnej epoki.

Rozwiązane ćwiczenia

Ćwiczenie 1

Linia lotnicza musi przenieść 1535 osób. Wiadomo, że przy 3 samolotach zabranie do ostatniego pasażera do miejsca docelowego zajęłoby 12 dni. 450 więcej osób dotarło do linii lotniczych, a 2 samoloty mają na celu współpracę z tym zadaniem. Ile dni zabierze linia lotnicza do ostatniego pasażera do miejsca docelowego?

Związek między liczbą ludzi a dniami pracy jest bezpośredni, ponieważ im więcej osób będzie wymagało więcej dni, aby wykonać tę pracę.

Z drugiej strony związek między samolotami i dniami jest odwrotnie proporcjonalny. Zwiększając ilość samolotów, niezbędne dni spadają, aby przenieść się do wszystkich pasażerów.

Tabela wartości odnoszących się do tej sprawy jest przeprowadzana.

Jak wyszczególniono w początkowym przykładzie, licznik i mianownik muszą być zainwestowane w ułamek odpowiadający zmiennej odwrotnej w odniesieniu do nieznanego. Pozostawienie operacji w następujący sposób:

Może ci służyć: obliczanie podejść z wykorzystaniem różnicowych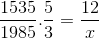

X = 71460/7675 = 9,31 dni

Aby przeprowadzić się do 1985 osób korzystających z 5 samolotów, konieczne jest ponad 9 dni.

Ćwiczenie 2

25 -pistonowe zbiory kukurydzy są zabierane do ciężarówek towarowych. Wiadomo, że poprzedni rok zajęła 8 godzin z płacą 150 pracowników. Jeśli w tym roku lista płac wzrośnie o 35%, ile czasu zajmie wypełnienie ciężarówek zbiorczych 40 -postu?

Przed przedstawieniem tabeli wartości należy zdefiniować liczbę pracowników w tym roku. To zwiększyło 35% początkowej liczby 150 pracowników. W tym celu stosuje się bezpośrednią trzy reguły.

100% - 150

35% - x

X = (35 . 100)/100 = 52,5. Jest to liczba dodatkowych pracowników w odniesieniu do poprzedniego roku, uzyskując całkowitą liczbę 203 pracowników, niezadowolonych z uzyskiwanej kwoty.

Odpowiednia tabela danych jest zdefiniowana

W tym przypadku waga reprezentuje bezpośrednią zmienną relacji z nieznanym czasem. Z drugiej strony zmienna pracowników zarządza odwrotną relacją z czasem. Większa liczba pracowników, dzień będzie krótszy.

Biorąc pod uwagę te rozważania i inwestując ułamek odpowiadający pracownikom, jest to obliczane.

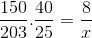
X = 40600 /6000 = 6,76 godziny

Dzień potrwa nieco mniej niż 7 godzin.

Proponowane ćwiczenia

- Zdefiniuj 73% z 2875.

- Oblicz ilość godzin śpi Teresa, jeśli wiadomo, że tylko 7% całkowitego snu. Zdefiniuj, ile godzin spać w tygodniu.

- 2000 publiczna gazeta co 5 godzin, używając tylko 2 maszyn do drukowania. Ile kopii wyprodukuje za 1 godzinę, jeśli używasz 7 maszyn? Jak długo wyprodukuje 10.000 kopie za pomocą 4 maszyn?

Bibliografia

1. Encyklopedia alvarez-iniciacion. DO. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
2. Kompletny podręcznik podstawowej instrukcji elementarnej i doskonałej: do wykorzystania wnioskodawców do nauczycieli, a zwłaszcza uczniów normalnych szkół prowincji, tom 1. Joaquín Avendaño. Drukowanie d. Dionisio Hidalgo, 1844.
3. Przybliżenie oceny rzeczywistych funkcji. P. P. Petreshev, Vasil Atanasov Popov. Cambridge University Press, 3 marca. 2011.
4. Arytmetyka żywiołowa do nauczania w szkołach i szkołach w Ameryce Środkowej. Darío González. Wskazówka. Arenales, 1926.
5. Studium matematyki: na temat studiów i trudności matematyki. Augustus de Morgan. Baldwin and Cradock, 1830.