Produkt krzyżowy

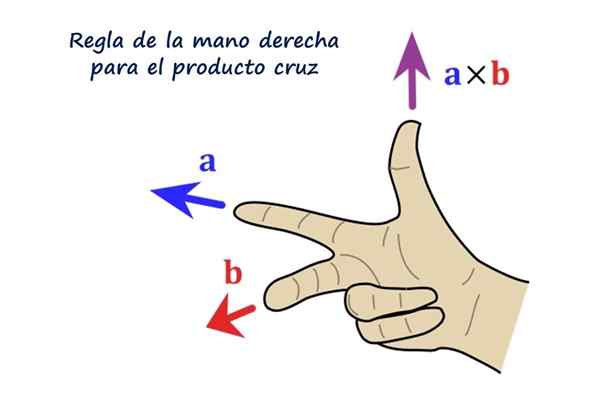Właściwa zasada dla produktu wektorowego. Źródło: f. Zapata.

Jaki jest produkt krzyżowy lub produkt wektorowy?

On Produkt krzyżowy, Nazywany również produktem wektorowym, jest to rodzaj produktu, który jest przeprowadzany między dwoma wektorami i powoduje inny wektor, prostopadły do ​​płaszczyzny zdefiniowanej przez pierwsze dwa.

Produkt krzyżowy między dowolnymi dwoma wektorami Do I B, Powoduje inny wektor R, matematycznie jest napisane w następujący sposób:

Do × B = R

Brzmi to: „Cruz B równy R ".

W tekście drukowanym wektory są napisane od odważnych tekstów lub strzałką na liście, aby odróżnić je od ich wielkości lub modułu. Do tego są używane, zamiennie, słupki modułowe i bieżące litery, więc bezwzględna wartość wektora Do Symbol jest napisany w ten sposób:

│Do│ = a

Wartość bezwzględna lub moduł produktu wektora między dwoma wektorami jest obliczany przez pomnożenie modułu obu wektorów przez kąt θ:

R = a ∙ b ∙ sen θ

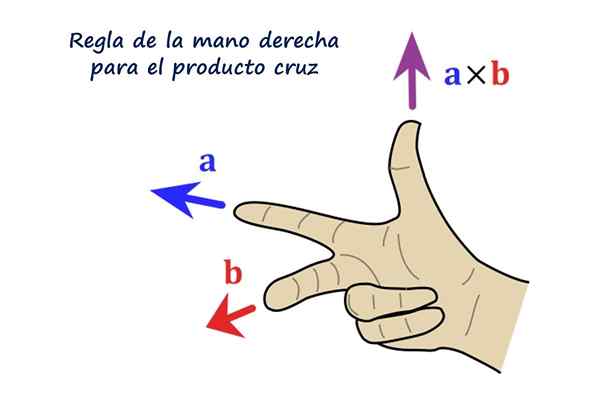
Kierunek wektora R Jest prostopadle do wektorów Do I B. Poczucie R To jest dekstrogyr Do w kierunku B I w praktyce określa się to za pomocą zasady prawej ręki, która polega na ustawianiu indeksu, średniego i kciuka prawej ręki w następujący sposób:

• Palec wskazujący jest umieszczony po wektorze Do
• Z środkowym palcem podąża za wektorem B
• Kciuk, rozszerzony, wskazuje kierunek i kierunek wektora R.

Tego zamówienia należy dokładnie przestrzegać, ponieważ produkt wektorowy nie jest przedmiotem pracy, to znaczy Do × B ≠ B × Do A jeśli wektory zostaną wymienione, właściwy wynik nie zostanie uzyskany.

Może ci służyć: twierdzenie o istnieniu i wyjątkowości: demonstracja, przykłady i ćwiczenia

Czytelnikowi zaleca się umieszczenie prawej ręki, jak pokazuje rysunek, wskaźnik wskazujący w lewo reprezentuje wektor Do, Środkowy palec następuje B I wskazuje bezpośrednio na czytelnika, wreszcie kciuk wskazuje, wskazując na kierunek i kierunek wektora Do × B = R.

Właściwości produktu Cruz

-Produkt krzyżowy lub wektorowy między dwoma wektorami zawsze powoduje inny wektor.

-Dlatego produkt krzyżowy nie jest do pracy: Do × B ≠ B × Do.

-Dla produktu krzyżowego prawdą jest: Do × B = - (B × Do). Ta właściwość nazywa się Antykonmin.

-Powstały wektor produktu wektora między dwoma wektorami jest prostopadle (normalny) do wspomnianych wektorów.

-Z powyższego wynika, że ​​produkt wektorowy między wektorami o tym samym kierunku jest zerowy. W szczególności Do × A = 0.

-Produkt krzyżowy jest zgodny z prawem dystrybucyjnym w odniesieniu do sumy: Do × (B+C) = Do × B + Do × C

-Jeśli M jest skalarnym, to m (Do × B) = m Do × B = Do × m B

Produkt między wektorami jednostkowymi

Trzy wektory jednostkowe, nazywane Siema, J I k, Są prostopadłe do siebie i wskazują trzy znaczące kierunki przestrzeni: wysokie, szerokie i głębokość. Te adresy są prostopadłe do siebie.

Produkt wektorowy między wektorami jednostkowymi jest łatwo określany na podstawie zasady prawej ręki i pamięta o właściwościach produktu krzyżowego:

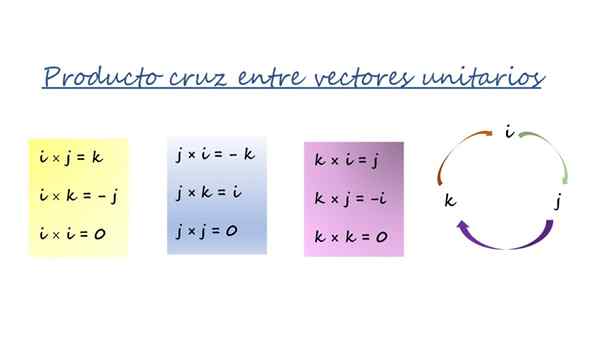Produkt wektorowy wektorów jednostkowych kartezjańskich. Źródło: f. Zapata.

Trzy kolorowe pudełka na rysunku są podsumowane w rundzie strzałkami po prawej stronie i są używane w ten sposób:

-Podczas mnożenia w kierunku strzałki wynik jest wektorem przed strzałką i ma znak dodatni. Na przykład poprzez pomnożenie wektorowe J I k, Trzeci wektor to Siema, A gdy zamówienie podąża za znaczeniem strzałki, znak jest +.

Może ci służyć: funkcje wektorowe

-A jeśli mnoży się w przeciwnym kierunku do strzałki, wynik jest trzeci wektor przed strzałką, ale z znakiem ujemnym.

Wektory jednostkowe stanowią podstawę, więc każdy inny wektor może być napisany w zakresie. To znacznie ułatwia obliczenie produktu krzyżowego między dwoma dowolnymi wektorami w przestrzeni.

Jak analizować produkt krzyżowy dwóch wektorów analitycznie

Kiedy wektory Do I B Mają dowolny kierunek w przestrzeni, z komponentami wzdłuż każdego z nich, łatwiej jest obliczyć produkt krzyżowy w sposób analityczny, wyrażając je pod względem wektorów jednostkowych Siema, J I k:

• Do = a_X Siema + Do_I J + Do_z k
• B = b_X Siema + B_I J + B_z k

Teraz stosuje się właściwość dystrybucyjną mnożenia, która jest również ważna dla produktu krzyżowego:

Do × B = (a_X Siema + Do_I J + Do_z k) × (b_X Siema + B_I J + B_z k) =

= (a_X Siema × b_X Siema) + (a_X Siema × b_I J) + (a_X Siema × b_z k) + (a_I J × b_X Siema) + (a_I J × b_I J) + (a_I J × b_z k) + (a_Z k × b_X Siema) + (a_Z k × b_I J) + (a_Z k × b_z k)

Produkty między równymi wektorami jednostkowymi są anulowane, ponieważ są to wektory równoległe, co zmniejsza to wyrażenie do 6 terminów:

Do × B = (a_X Siema × b_I J) + (a_X Siema × b_z k) + (a_I J × b_X Siema) + (a_I J × b_z k) + (a_Z k × b_X Siema) + (a_Z k × b_I J)

Wreszcie, używając powyższego rysunku, każdy produkt daje:

Do × B = a_X B_I k + Do_X B_z ( -J) + a_I B_X ( -k) + a_I B_z Siema + Do_Z B_XJ + Do_Z B_I ( -Siema) =

= (a_I B_z - A_Z B_I) Siema + (Do_Z B_X - A_X B_z) J + (Do_X B_I - A_I B_X) k

Produkt Cruz przez wyznacznik

Nie jest konieczne zapamiętywanie powyższego wzoru, ale wygodne zastosowanie rundy poprzedniej figury lub po prostu uważnie wykonanie wyznacznika pokazanego poniżej, co jest całkowicie równoważne:

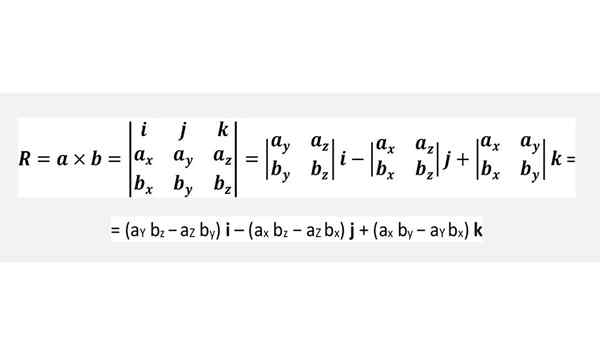
Przykład

Zakładanie wektorów Do I B Czy:

• Do = 5 Siema - J + 4 k
• B = -Siema + 0J +7 k

Produkt między nimi jest obliczany poprzez identyfikację i zastępowanie odpowiednich współrzędnych:

Może ci służyć: hiperboliczny paraboloid: definicja, właściwości i przykłady

Do_X = 5; Do_I = −1; Do_z = 4; B_X = −1; B_I = 0: B_z = 7

Do × B = [(−1) ∙ 7 - 4 ∙ 0] Siema + [(4 ∙ (-1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] k = [−7 - 0] Siema + [(-4–35) J + [0 - 1] k =

= (−7) Siema - 39 J - k

Metoda determinująca oferuje ten sam wynik.

Ćwiczenia

Oblicz według determinantów, produkt krzyżowy wśród wektorów:

• Lub = 2 Siema +J + 5 k
• v = Siema + 4J +7 k

I określ obszar równoległoboku substancji przez poprzednie wektory, jak pokazano na rysunku:

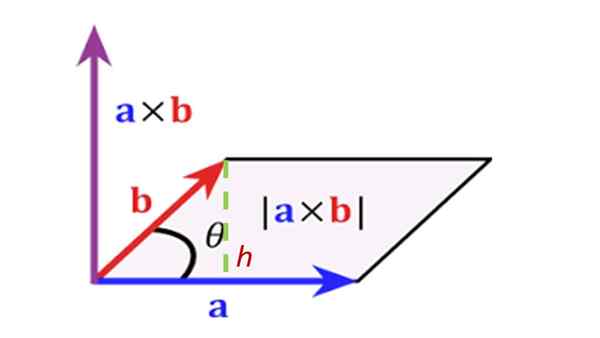
Rozwiązanie

Wartości współrzędnych wektorów są zastępowane w wyznaczniku:

Określony obszar równoległoboku jest modułem produktu wektorowego między nimi, co spowodowało: R = 17,3 jednostki.