Kwadratowy pryzmat

Wyjaśniamy, jaki jest czworokątny pryzmat, jego cechy, twarze, wierzchołki, krawędzie, jak obliczyć objętość, przykłady i ćwiczenia rozstrzygnięte

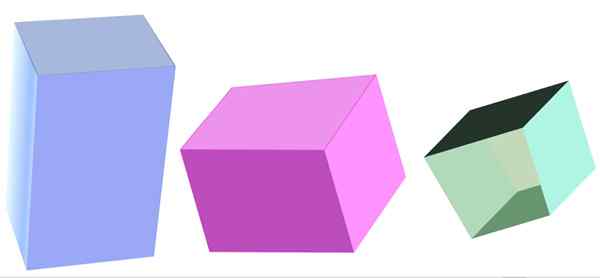
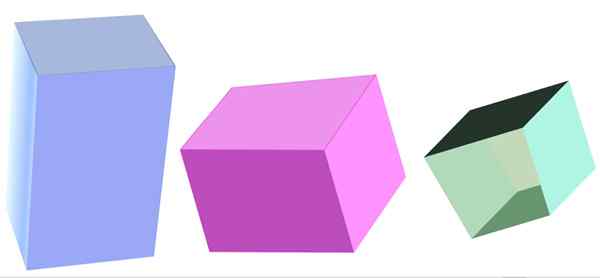Różne rodzaje czworokątnego pryzmatu. Źródło: f. Zapata

Co to jest czworokątny pryzmat?

On Kwadratowy pryzmat Jest to trójwymiarowa geometryczna postać rodziny Polyhedros. Składa się z dwóch równych i równoległych twarzy, z kształtem czworoboku, jako podstawy i czterech równoległoboków po bokach, w sumie sześć twarzy.

Istnieje kilka kryteriów ich klasyfikacji, ponieważ istnieje wiele możliwości kształtu twarzy i skłonności. Na przykład są Proste domowe pryzmaty i Nachylone czworokątne pryzmaty.

W pierwszym przypadku boki są prostopadłe do podstawy, a następnie są prostokątami lub kwadratami. W drugim przypadku twarze boczne są pochylone w odniesieniu do podstawy, dlatego nie mogą być prostokątami ani kwadratowymi.

Ponadto pryzmat czworokątny może być regularny lub nieregularny, w zależności od podstawy jest regularnym lub nieregularnym czworobocznym. Zwykle czworobok jest kwadratem, którego cztery strony i jego cztery kąty mierzą to samo .

Przykładem specjalnego pryzmatu Home Run jest równoległość, której podstawy są równoległobokami. Kształty pudełek i cegieł są inspirowane kwadranżnymi pryzmatami, więc dobre przykłady używania tej geometrycznej figury w praktycznych zastosowaniach.

Charakterystyka czworokątnego pryzmatu

Do najważniejszych cech czworokątnego pryzmatu są:

• Ich twarze mają kształt wielokąta.
• Ma w sumie 6 twarzy (2 bazy i 4 strony), 12 krawędzi lub krawędzi i 8 wierzchołków (rogi).
• Boczne twarze można kształtować, takie jak: kwadrat, prostokąt, równoległobok, romb lub romboid.
• Jego boki mogą być proste (formularz 90º kąt z zasadami) lub nachylony (po stronie wewnętrznej jest kąt mniejszy niż 90º).
• Boczne twarze prostych pryzmatów mogą być tylko kwadratowe lub prostokąty.
• Podstawy pryzmatu również otrzymują nazwę wytyczne.
• Jeśli podstawa jest regularna czworokątna, czworokątny pryzmat jest również regularny. Ponieważ płaska liczba jest regularna, jeśli wszystkie jej boki mają tę samą miarę, jedyną możliwością jest to, że podstawy są kwadratowe.
• Gdy podstawa pryzmatu jest jakakolwiek inna czworobok inna niż kwadrat, wówczas pryzmat jest uważany za nieregularny.
• Regularny czworokątny pryzmat można zarejestrować w cylindrze.

Może ci służyć: statystyki wnioskowania: historia, cechy, do czego służy przykłady

Elementy czworokątnego pryzmatu

Pięć elementów czworokątnego pryzmatu jest wspólne dla wszystkich pryzmatów:

• Bazy, składane przez dwa identyczne i równoległe czworokątne.
• Boczne twarze, to cztery równoległoboki, które graniczą z figurą.
• Wierzchołki lub rogi, wspólne punkty, które mają trzy sąsiednie strony pryzmatu.
• Krawędzie lub krawędzie, wspólny segment, który ma dwie sąsiednie twarze.
• Wysokość: Jest to długość prostopadłego odcinka z końcami w podstawach. Kiedy pryzmat jest prosty, wysokość pokrywa się z miarą bocznych krawędzi.
• Prosta sekcja, obszar skrzyżowania pryzmatu i płaszczyzny, który tworzy 90º z bocznymi krawędziami.

Poniższy obraz pokazuje każdy z tych elementów dla prostego czworokątnego pryzmatu:

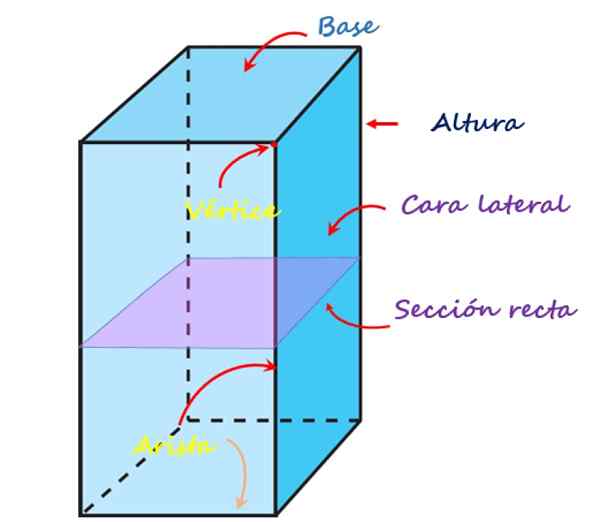Elementy czworokątnego pryzmatu. Źródło: f. Zapata

Twarze, wierzchołki i krawędzie

Ogromne znaczenie dla badania pryzmatu czworokątnego to twarze, wierzchołki i krawędzie:

Twarze

Twarze pryzmatu stanowią w sumie 6: 2 identyczne zasady w kształcie czworoboku i 4 bocznych stron lub twarzy w formie równoległobokowej.

Wierzchołki

Są to rogi figury, punkt, w którym przychodzą trzy sąsiednie twarze.

Krawędzie

Są to segmenty skrzyżowań między twarzami pryzmatu. Krawędzie są klasyfikowane jako:

• Krawędzie podstawowe, Wspólne segmenty między bazami i bocznymi twarzami.
• Boczne krawędzie, Jak sama nazwa wskazuje, są to wspólne segmenty wśród twarzy bocznych.

Górna rysunek pokazuje dwa rodzaje krawędzi, oznaczone różnymi strzałkami kolorystycznymi. Liczba krawędzi n_DO można określić za pomocą Twierdzenie Euler z wielościów, który odnosi liczbę krawędzi do twarzy n_C i wierzchołki n_V:

Może ci służyć: funkcje matematyczne

N_DO = N_C + N_V −2

Dla czworokątnego pryzmatu n_C = 6 i n_V = 8, dlatego:

N_DO = 6 + 8 −2 = 12

Stąd liczba krawędzi lub krawędzi czworokątnego pryzmatu wynosi 12.

Jak obliczyć objętość czworokątnego pryzmatu?

Objętość pryzmatu jest rozumiana jako część zablokowanej przez nią części przestrzeni i jest mierzona w jednostkach sześciennych, które mogą być metrami sześciennymi, centymetry sześcienne, stopy sześcienne lub inne odpowiednie, pod warunkiem, że są one długie dla kostki.

Tom V jest zawsze dodatnią ilością, aw przypadku każdego czworokątnego pryzmatu jest podawany przez produkt między podstawą podstawy do_B i wysokość h:

V = a_B × H

SIEMA) Regularna ilość czworokątna pryzmat

Ponieważ podstawy są kwadratowe, a kwadrat kwadratu jest boczny ℓ kwadrat:

DO_B = ℓ²

Następnie objętość pryzmatu, którego wzrost jest „h”, wynosi:

V = ℓ² × H

Ii) Nieregularna czterokrotna objętość pryzmatu

Zależy to od kształtu podstawy i wysokości „h” pryzmatu:

1.- Prostokątny pryzmat podstawowy

Obszar boków prostokąt „A” i „B” to:

DO_B = A × B

Więc tom jest:

V = a × b × h

2.- Romboidalny pryzmat podstawowy

Obszar Rombus jest półproduktem jego przekąt „D” i „D”:

A tom jest:

3.- Romboid -podstawowy pryzmat

Obszar podstawowy w kształcie Rhomboid jest produktem jego podstawy „B” i jego względnej wysokości ”H_R„Do tej podstawy, która jest segmentem prostopadłym, który przechodzi od tej podstawy do równoległej do niej.

DO_B = B × H_R

Stąd objętość pryzmatu z tą bazą wynosi:

Może ci służyć: jaki jest zakres statystyk? (Z przykładami)

V = b × h_R × H

4.- Trapezoidalny pryzmat podstawowy

Ponieważ obszar trapezoidów jest pół miejsca równoległych boków „A” i „B”, pomnożony przez jego wysokość „C”:

Objętość trapezoidalnego pryzmatu wynosi:

5.- Podstawowy pryzmat w kształcie trapezu

Obszar symetrycznego trapezu jest półproduktem jego przekątnych D i D, dlatego:

W tym przypadku objętość pryzmatu wynosi:

Ćwiczenie rozwiązane

Trapezoidalny pryzmat podstawy ma objętość 648 cm³. Równoległe strony miary trapezoidów a = 10 cm i b = 5 cm, podczas gdy wysokość trapezu wynosi c = 6 cm. Z tymi danymi znajdź wysokość pryzmatu.

Rozwiązanie

Ponieważ mają wymiary podstawy, Twój obszar można łatwo obliczyć:

I formuły:

V = a_B × H

„H” jest oczyszczone, wysokość pryzmatu, ponieważ jego tom jest znany:

H = v/ a_B = 648 cm³ / 45 cm² = 14.4 cm

Przykłady

Prostokątny pryzmat lub kostka

Sześć twarzy tego prostego pryzmatu są kwadratowe lub prostokątne. Pudełka są przykładami prostokątnych pryzmatów, formy używanej również w wielu obiektach i konstrukcjach, takich jak budynki.

Sześcian

Kostka to regularny czworokątny pryzmat, którego sześć stron ma kształt, na przykład kostkę lub dobrze znana gra Rubika.

Kostka jest częścią grupy platońskich stałych, geometrycznych postaci, które spełniają dwa warunki. Po pierwsze, każda twarz jest zwykłym wielokątem, a po drugie, że każdy wierzchołek ma wspólną taką samą liczbę twarzy.

Kostka spełnia oba warunki, ponieważ ich twarze mają kwadratowy kształt, który jest zwykłym wielokątiem. I w każdym z ośmiu wierzchołków kostki trzy twarze tego samego zbieżności.

Pozostałe stałe platońskie to tetrahedron, oktaedron, Dodekahedro i Icosaedro.