Objaśnienie ciśnienia manometrycznego, wzory, równania, przykłady

ciśnienie miernika P_M Jest to zmierzone w stosunku do ciśnienia odniesienia, które w większości przypadków jest wybierane jako ciśnienie atmosferyczne P_bankomat Na poziomie morza. To jest wtedy Presja względna, Kolejny termin, dla którego jest również znany.

Innym sposobem, w jaki zwykle mierzy się ciśnienie, jest porównanie go z bezwzględną pustką, której ciśnienie jest zawsze zerowe. W tym przypadku mówi się o presja bezwzględna, do którego będziemy oznaczać, w jaki sposób p_Do.

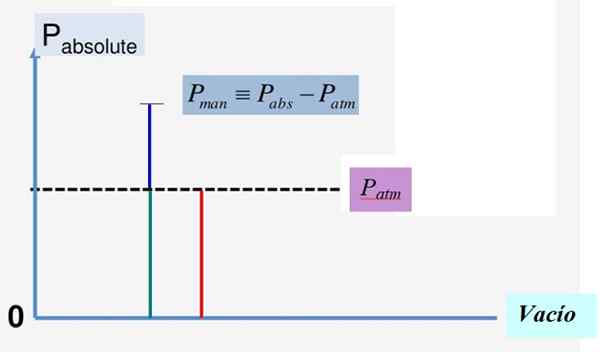
Rysunek 1. Ciśnienie bezwzględne i ciśnienie manometryczne. Źródło: f. Zapata.

Związek matematyczny między tymi trzema ilościami to:

P_Do = P_bankomat + P_M

Dlatego:

P_M = P_Do - P_bankomat

Rysunek 1 wygodnie ilustruje tę relację. Ponieważ ciśnienie próżniowe wynosi 0, ciśnienie bezwzględne jest zawsze dodatnie i to samo dotyczy ciśnienia atmosferycznego P_bankomat.

Ciśnienie manometryczne jest zwykle stosowane do oznaczania ciśnienia powyżej ciśnienia atmosferycznego, takiego jak przenoszone przez opony lub na dnie morza lub basen, który wywiera na masę kolumny wody. W takich przypadkach p_M > 0, od p_Do > P_bankomat.

Poniżej presja bezwzględna jest bezwzględna presja_bankomat. W takich przypadkach p_M < 0 y recibe el nombre de ciśnienie próżniowe I nie należy go mylić z ciśnieniem już opisanej próżni, jakim jest brak cząstek zdolnych do wywierania ciśnienia.

[TOC]

Wzory i równania

Ciśnienie w płynie -likwidowym lub gazowym -jest jedną z najważniejszych zmiennych w jego badaniu. W płynie stacjonarnym ciśnienie jest takie samo na wszystkich punktach do tej samej głębokości, niezależnie od orientacji, podczas gdy ruch płynów w rurach jest spowodowany zmianami ciśnienia.

Średnie ciśnienie definiuje się jako iloraz między siłą prostopadłą do powierzchni F_⊥ oraz obszar wspomnianej powierzchni A, który jest wyrażany matematycznie w następujący sposób:

P = f_⊥ /DO

Ciśnienie jest wielkością skalarną, której wymiary są siły na jednostkę powierzchni. Jednostki twojej miary w systemie jednostek międzynarodowych (SI) to Newton/M², Nazywany Pascal i skrócony jako PA, na cześć Blaise Pascal (1623-1662).

Wielokrotności jak kilogram (10³) I Mega (10⁶) Są często używane, ponieważ ciśnienie atmosferyczne jest zwykle w zakresie 90.000 - 102.000 PA, co jest równe: 90 - 102 kPa. Naciski rzędu Mega Pascals nie są rzadkie, więc ważne jest zapoznanie się z prefiksami.

W jednostkach anglo -syxon ciśnienie jest mierzone w funtach/stopie², Jednak powszechną rzeczą jest wykonanie w funtach/calach² albo psi (Funts Force na cal kwadratowy).

Może ci służyć: transfer ciepła: prawa, formularze transmisji, przykłady

Zmienność ciśnienia z głębokością

Im więcej zanurzamy się w wodzie basenu lub w morzu, tym większa presja doświadczamy. Przeciwnie, rosnąca wysokość, ciśnienie atmosferyczne zmniejsza się.

Średnie ciśnienie atmosferyczne na poziomie morza ustalono w 101300 PA lub 101.3 kPa, podczas gdy w Mariana Pit na zachodnim Pacyfiku - największa znana głębokość - jest około 1000 razy wyższa, a na szczycie Everestu jest zaledwie 34 kPa.

Oczywiste jest, że ciśnienie i głębokość (lub wysokość) są powiązane. Aby wiedzieć w przypadku płynu spoczynkowego (równowaga statyczna) jest uważany za część płynu z płynem w kształcie dysku, ograniczonym w pojemniku (patrz ryc. 2). Dysk ma przekrój DO, waga DW i wysokość Dy.

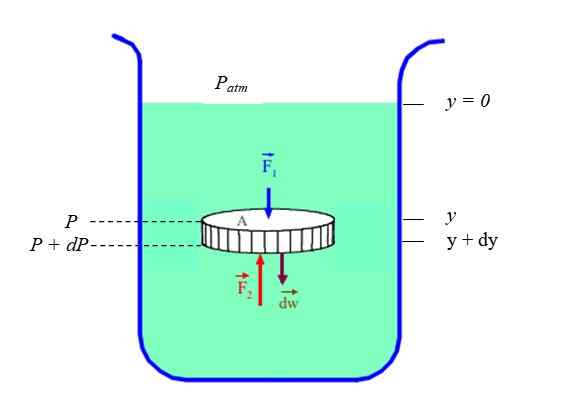Rysunek 2. Różnicowy element statycznego płynu równowagi. Źródło: Fanny Zapata.

Zadzwonimy P pod presją, która istnieje dogłębnie ”I" I P + DP pod presją, która istnieje dogłębnie (i + dy). Ponieważ gęstość ρ płynu jest przyczyną jego masy DM i jego objętość DV, Musisz:

ρ = DM/ DV ⇒ DM = ρ.DV

Dlatego waga DW elementu to:

dw = g. DM = ρ.G.DV

A teraz ma zastosowanie drugie prawo Newtona:

Σ f_I = F₂ - F₁ - DW = 0

(P + DP).A - p.DO - ρ.G.DV = 0

(P + DP).A - p.DO - ρ.G. DO. Dy = 0

DP = ρ.G.Dy

Rozwiązanie równania różniczkowego 

Integracja obu stron i biorąc pod uwagę tę gęstość ρ, a także grawitacja G Są stałe, jest poszukiwane wyrażenie:

P₂ - P₁ = ΔP = ρ.G.(I₂ - I₁)

ΔP = ρ.G. ΔI

Jeśli w poprzednim wyrażeniu jest wybrane P₁ takie jak ciśnienie atmosferyczne i I₁ Tak jak powierzchnia cieczy I₂ Znajduje się na głębokości H I ΔP = p₂ - P_bankomat Jest to ciśnienie manometryczne w zależności od głębokości:

P_M = ρ.G.H

Jeśli potrzebujesz wartości ciśnienia bezwzględnego, ciśnienie atmosferyczne jest po prostu dodawane do poprzedniego wyniku.

Przykłady

W przypadku ciśnienia manometrycznego stosuje się urządzenie ciśnieniomierz, które ogólnie oferują różnice na ciśnienie. Ostatecznie zostanie opisana zasada działania manometru ulegającego ciśnieniu u -ulegającym, ale teraz zobaczmy kilka ważnych przykładów i konsekwencji wcześniej odliczonego równania.

Zasada Pascal

Równanie ΔP = ρ.G.(I₂ - I₁) Można to zapisać jako  P = PO + ρ.G.H, Gdzie P jest ciśnieniem na głębokości H, chwila P_albo Zwykle jest to ciśnienie na powierzchni płynu P_bankomat.

Oczywiście za każdym razem, gdy się zwiększasz PO, wzrasta P w tej samej ilości, o ile jest to płyn, którego gęstość jest stała. Właśnie to miała rozważyć ρ stałe i umieść go poza całką rozwiązywaną w poprzednim rozdziale.

Może ci służyć: prosty ruch harmoniczny

Zasada Pascal stwierdza, że ​​każdy wzrost ciśnienia płynu ograniczonego w równowadze jest przenoszony bez żadnych zmian na wszystkie punkty wspomnianego płynu. Dzięki tej właściwości można pomnożyć siłę F₁ zastosowane do małego lewej lewicy i uzyskaj F₂ po prawej.

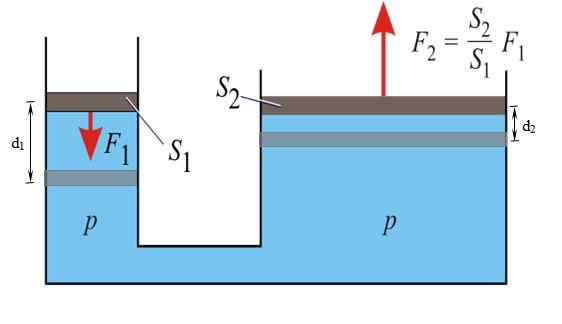Rysunek 3. W prasie hydraulicznej stosuje się zasadę Pascal. Źródło: Wikimedia Commons.

Hamulce samochodowe działają zgodnie z tą zasadą: do pedału stosuje się stosunkowo niewielką siłę, która staje się główną siłą na cylindrze hamulcowym na każdym kole, dzięki płynowi stosowanemu w układzie systemowym.

Hydrostatyczny paradoks Stevina

Hydrostatyczny paradoks stwierdza, że ​​siła spowodowana ciśnieniem płynu na dole pojemnika może być równa, większa lub mniejsza niż masa samego płynu. Ale podczas umieszczania pojemnika na skalę zwykle rejestruje masę płynu (plus oczywiście jeden z pojemników). Jak wyjaśnić ten paradoks?

Zaczynamy od faktu, że ciśnienie na dole pojemnika zależy wyłącznie od głębokości i jest niezależne od formy, jak wydedukowano w poprzedniej sekcji.

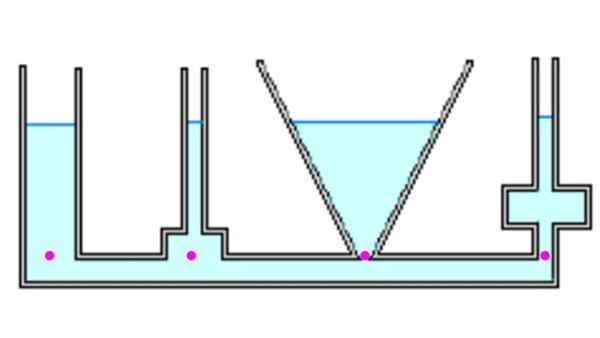Rysunek 4. Ciecz osiąga tę samą wysokość we wszystkich pojemnikach, a ciśnienie w tle jest takie same. Źródło: f. Zapata.

Spójrzmy na różne pojemniki. Po komunikacji, gdy są wypełnione płynem, wszyscy osiągają tę samą wysokość H. Widoczne punkty mają tę samą presję, ponieważ są na tej samej głębokości. Jednak siła spowodowana ciśnieniem w każdym punkcie może różnić się od wagi (patrz przykład 1 poniżej).

Ćwiczenia

Ćwiczenie 1

Porównaj siłę wywieraną przez ciśnienie na dnie każdego z pojemników z ciężarem płynu i wyjaśnij, dlaczego z różnic, jeśli istnieją jakieś.

Kontener 1 

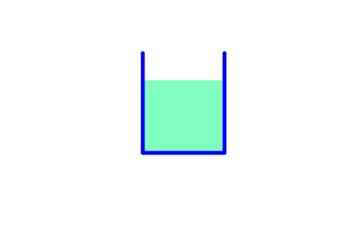Rysunek 5. Ciśnienie w tle jest takie samo w wielkości dla masy płynu. Źródło: Fanny Zapata.

W tym pojemniku obszar podstawowy jest zatem:

Waga płynu: Mg = ρ.V.G = ρ . DO .H . G

Nacisk na dole: ρ. G. H

Siła z powodu nacisku: F = P.A = ρ. G. H. DO

Waga i siła z powodu ciśnienia są równe.

Kontener 2 

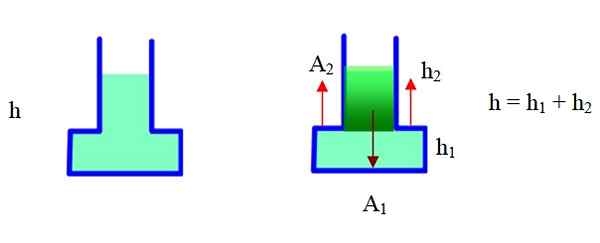Rysunek 6. Siła spowodowana ciśnieniem w tym pojemniku jest większa niż waga. Źródło: f. Zapata.

Pojemnik ma wąską część i szeroką część. W odpowiednim schemacie został podzielony na dwie części i użyje geometrii, aby znaleźć całkowitą objętość. Obszar a₂ jest zewnętrzny w stosunku do kontenera, h₂ Jest to wysokość wąskiej części, h₁ Jest to wysokość szerokiej części (podstawa).

Może ci służyć: Pleiades: historia, pochodzenie i kompozycja

Pełna objętość to objętość podstawy + objętość wąskiej części. Z tymi danymi masz:

Waga płynu: m . G = ρ . G. V = ρ . G. [DO₁ .H₁+ (DO₁ -DO₂) .H₂] =

= ρ . g (a₁.ha₂H₂) = ρ . G . DO₁.H - ρ . G . DO._. H₂ (Zastosowanie h = h₁ +H₂)

Nacisk na dno: p = ρ. G. H

Siłę na dole z powodu ciśnienia: F = P. DO₁ = ρ. G. H. DO₁

Porównując wagę płynu z siłą ze względu na ciśnienie, zauważa się, że jest to większe niż waga.

To, co się dzieje. Ta siła przeciwdziałająca dla osób wywieranych i wagi zarejestrowana w skali jest wynikiem tego. Zgodnie z tym wielkość wagi wynosi:

W = siła na tle - siła na rozłożonej części = ρ . G . DO₁.H - ρ . G . DO._. H₂

Ćwiczenie 2

Rysunek pokazuje manometrów otwartych rurki. Składa się z rurki U, w której jeden z końców jest pod ciśnieniem atmosferycznym, a drugi łączy się z S, układem, którego ciśnienie zostanie zmierzone.

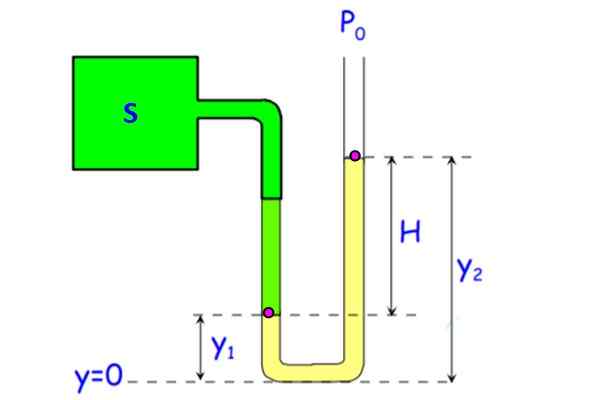Rysunek 7. Otwarta manometra rurki. Źródło: f. Zapata.

Ciecz w rurce (na żółto na rysunku) może być woda, chociaż rtęć służy do zmniejszenia wielkości urządzenia. (Różnica 1 atmosfery lub 101.3 kPa wymaga 10 kolumny wodnej.3 metry, nic przenośnego).

Zwracane jest znalezienie ciśnienia manometrycznego P_M W systemie S, w zależności od wysokości h kolumny ciekłej.

Rozwiązanie

Ciśnienie w tle dla obu gałęzi rurki jest takie same, ponieważ jest na tej samej głębokości. Niech p_DO Presja w punkcie A, znajdująca się w i₁ I p_B te z punktu B, który jest na wysokości i₂. Ponieważ punkt B znajduje się w interfejsie płynu i powietrza, ciśnienie jest P_albo. W tej gałęzi miernika ciśnienia ciśnienie na dole wynosi:

PO + ρ.G.I₂

Ze swojej strony ciśnienie u dołu dla gałęzi lewej to:

P + ρ.G.I₁

Gdzie p jest ciśnieniem bezwzględnym układu, a ρ jest gęstością płynu. Równe oba ciśnienia:

PO + ρ.G.I₂ = P +ρ.G.I₁

Clearing P:

P = PO + ρ.G.I₂ - ρ.G.I₁ = PO + ρ.g (i₂ - I₁) = PO + ρ.G. H

Dlatego ciśnienie manometryczne P_M Jest podawany przez P - p_albo = ρ.G. H I aby mieć swoją wartość, wystarczy zmierzyć wysokość, do której płyn manometryczny wznosi się i pomnoży przez wartość G i gęstość płynów.

Bibliografia

1. Cimbala, c. 2006. Mechanika płynów, podstaw i zastosowań. MC. Graw Hill. 66-74.
2. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 4. Płyny i termodynamika. Pod redakcją Douglas Figueroa (USB). 3-25.
3. Mott, r. 2006. Mechanika płynów. 4. Wydanie. Edukacja Pearsona. 53-70.
4. Shaugnessy, e. 2005. Wprowadzenie do mechaniki płynów.Oxford University Press. 51 - 60.
5. Stylianos, v. 2016. Do prostego wyjaśnienia klasycznego paradoksu hydrostatycznego. Odzyskane z: Haimgaifman.Akta.WordPress.com