Sześciokąta piramida

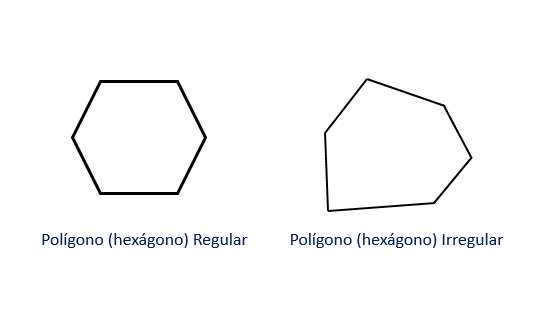
Rysunek 1. Po lewej stronie sześciokątna piramida i po prawej stronie jej siedem stron rozmieszczonych w samolocie: pośrodku sześciokątna i wokół sześciu trójkątnych twarzy. Źródło: f. Zapata.

Co to jest heksagonalna piramida?

Heksagonalna piramida to trójwymiarowa postać geometryczna, której baza Jest to sześciokąt (wielokąt sześcioosobowy), a także sześć twarze trójkątne, które są gromadzone na pewnej wysokości podstawy, w danym punkcie wierzchołek albo wierzchołek.

W sumie piramida sześciokątna ma siedem twarzy, jeśli podstawa jest bokiem, więc ma również w kształcie wielościanu w kształcie Hepthedron, słowo pochodzące z języka greckiego („hept” oznacza siedem).

Jeśli trójkąty, które tworzą boki, to izosceles, to znaczy, mają dwie równe strony i jedną inną, jest to prosta piramida. A jeśli oprócz tego sześciokąt bazy jest regularny, to jest to Regularna piramida sześciokąta, Jak pokazano na rycinie 1.

Kiedy sześciokąt bazy nie jest regularny lub trójkąty, które tworzą twarze, nie są izoscelesami, istnieje Obok heksagonalna piramida.

Charakterystyka sześciokątnej piramidy

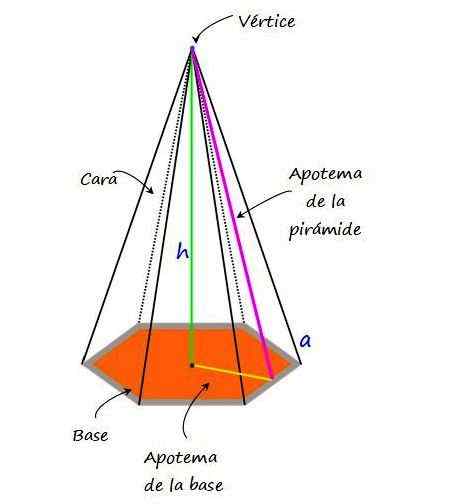Rysunek 2.- Heksagonalna piramida i jej główne elementy. Źródło: f. Zapata.

Główne cechy i elementy piramidy heksagonalnej są następujące:

-Baza, To sześciokąt, który może być regularny lub nieregularny.

-Twarze, Mają kształt trójkąta i w sumie 6.

-Wierzchołek lub wierzchołek piramidy, punkt okoliczności sześciu trójkątnych twarzy.

-Krawędź, segment, w którym pokrywają się dwie twarze piramidy. Boczne krawędzie Są to segmenty zbieżności twarzy bocznych, podczas gdy krawędzie bazy to segmenty, w których strona sześciokąta zbiega się i jedna strona sąsiedniego trójkąta. Na rycinie 2 krawędź jest oznaczona literą „A”.

Może ci służyć: podziały, w których pozostałość wynosi 300

-Wysokość, oznaczone jako „h”, jest to odległość mierzona od wierzchołka do podstawy piramidy.

-Pyramid Apotheme, segment, który dołącza do wierzchołka z punktem środkowym po jednej stronie podstawy.

-Podstawowy apoteme, Definiuje się tylko wtedy, gdy sześciokąt jest regularny. Składa się z segmentu, który dołącza do centrum sześciokąta z centrum jednej z jego stron.

Formuły dla obszaru i objętości

Pole powierzchni heksagonalnej piramidy, zarówno regularne, jak i nieregularne, jest obliczane przez dodanie obszarów bocznych twarzy i obszar sześciokątnej bazy:

A = a_baza + ∑a_{drogi strona}

W formule symbol „∑” reprezentuje sumę, aby podsumować sumę sześciu obszarów twarzy bocznych.

Dla zwykłej piramidy sześciokątnej istnieje formuła, aby znaleźć obszar:

A = 3l ∙ (AP_baza + AP_piramida)

Gdzie:

• L to krawędź podstawy (bok sześciokątny).
• AP_baza To apotem bazy
• AP_piramida To apotem piramidy.

Jeśli piramida nie jest regularna, ponieważ podstawa nie jest regularnym sześciokątem, ani ponieważ piramida jest ukośna, konieczne jest obliczenie obszarów każdego osobno, a następnie dodanie.

Regularna piramida sześciokątna ma również formułę do objętości:

V = l ∙ ap_baza∙ h

Tutaj „H” reprezentuje wysokość piramidy.

A jeśli piramida sześciokątna nie jest regularna, istnieje ogólna formuła, która ma zastosowanie do wszystkich piramid, do obliczenia jej objętości:

V = ⅓ ∙ a_baza ∙ h

Może ci służyć: rozkład liczb naturalnych (przykłady i ćwiczenia)

Przykład liczbowy

Dla zwykłej piramidy sześciokątnej, której wymiary to:

Baza Apothem: 4 cm

Długość krawędzi podstawy: 7 cm

Pyramid Apotheme: 15 cm

Wysokość: 10 cm

Oblicz następujące:

a) Sześciokątny obszar podstawowy.

b) powierzchnia piramidy.

c) objętość

Rozwiązanie

Obszar zwykłego sześciokąta to:

A = ½ (obwód × apotema) = ½ (6l × ap_baza)

A = 3l ∙ ap_baza  = 3 × 7 cm × 4 cm = 84 cm²

Rozwiązanie b

A = 3l ∙ (AP_baza + AP_piramida) = 3L ∙ AP_baza  + 3L ∙ AP_piramida = 84 cm² + (3 × 7 cm × 15 cm) = 399 cm².

Rozwiązanie c

Objętość można znaleźć w formule ogólnej:

V = ⅓ ∙ a_baza ∙ H = ⅓ ∙ 84 cm² ∙ 10 cm = 280 cm³

Jak zrobić sześciokątną piramidę?

Materiały

• Papier, karton lub karton.
• Reguła i drużyna
• Ołówek grafitu i kolorowe markery
• Nożyce
• Przyklej do rzemiosła.

Procedura

1. Przenieś szablon pokazany poniżej, w pożądanej skali, na tekturze lub tekturze, za pomocą ołówka grafitowego, reguły i drużyny. Inną opcją jest skopiowanie figury do typu dokumentu lub edytowalnego rysunku i powiększenie go, dopóki nie uzyskasz pożądanych wymiarów.
2. Po przeniesieniu szablonu na papier lub karton należy go wyciąć z wielką ostrożnością.
3. Teraz zgnij kropkowane linie, aby ukształtować piramidę, upewniając się, że boki poprawnie pasują.
4. Złóż także rzęsy, sprawdź, czy dobrze pasują, a następnie dodaj klej, starannie naciskając, aby były na miejscu, kształtując figurę.
5. Udekoruj piramidę kolorowymi markerami.

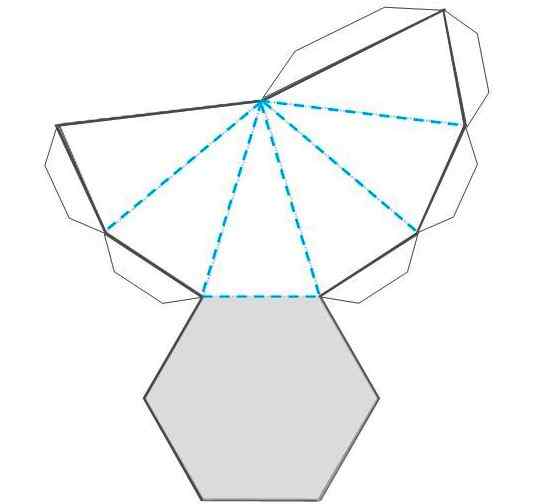Rysunek 3.- Szablon do cięcia i złożenia sześciokątnej piramidy. Źródło: f. Zapata.

Przykłady sześciokątnych piramid

Według podstawowego sześciokąta piramidy sześciokąta:

Może ci służyć: Język algebraiczny: koncepcja, po co to jest przykłady, ćwiczenia

-Wypukły, Jeśli wszystkie wewnętrzne kąty sześciokąta są mniejsze niż 180º.

-Wklęsły, Jeśli jeden lub więcej wewnętrznych kątów sześciokąta mierzy więcej niż 180º.

Regularna heksagonalna piramida na rycinie 1 jest wypukła, ponieważ wszystkie wewnętrzne kąty podstawy mierzą mniej niż 180º. Mówiąc dokładniej, wewnętrzne kąty zwykłego sześciokąta mierzą wszystkie 120º.

Zgodnie z tym kształt heksagonalnych piramid różni się, jak pokazano wtedy.

Obok heksagonalna piramida

Na obrazie ryc. 4 obserwuje się skośną piramidę sześciokątną, której podstawa jest regularna. Zwróć uwagę na trójkąt, który tworzy twarz na pierwszym planie, jest trójkątem z trzema różnymi stronami (trójkąt skaleny), w przeciwieństwie do piramidy na rycinie 1, której twarze są trójkąty izosceles. Jeśli linia jest rysowana z wierzchołka do środka sześciokątnego, okazuje się, że jest pochylona w odniesieniu do pionu.

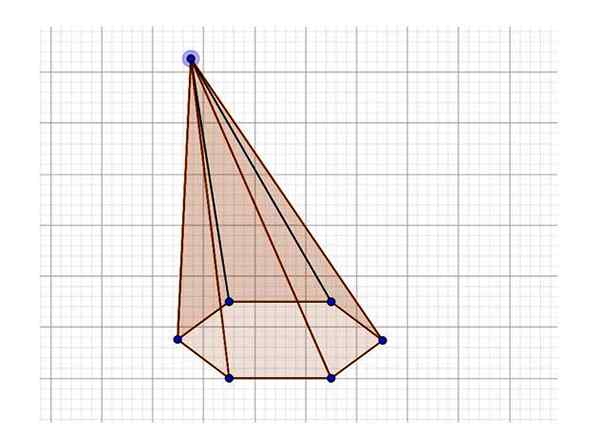Rysunek 4. Przykład ukośnej piramidy sześciokątnej. Źródło: f. Zapata przez Geogebra.

Kondłyk i ukośna piramida sześciokątna

Podstawa tej sześciokątnej piramidy zawiera kąt wewnętrzny, którego miara jest większa niż 180º, dlatego jest to wklęsła piramida, oprócz tego, że jest ukośna.

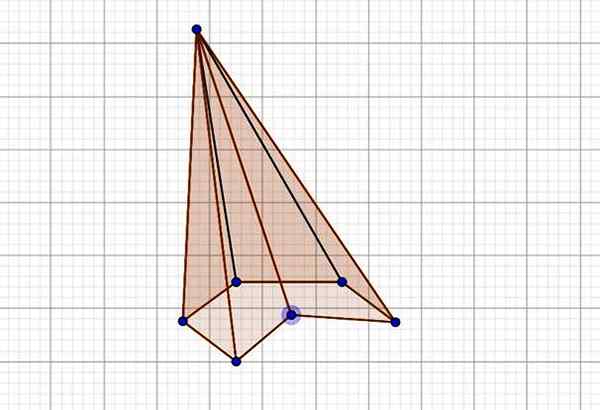Rysunek 5. Skośna i wklęsła sześciokątna piramida. Źródło: f. Zapata przez Geogebra.