W oczekiwaniu na wzór i równania linii, reprezentacja, przykłady

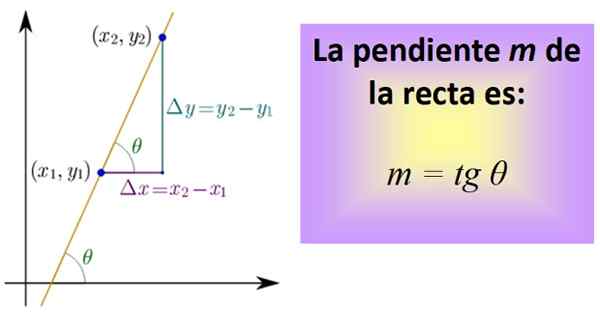
Oczekująca linia Styczna jest kąt θ, że ta linia tworzy się z osą poziomą, która przez konwencję jest mierzona w przeciwnym kierunku do dłoni zegara. Nachylenie dowolnej linii jest zawsze stałe i dlatego jest jedną z jego najważniejszych cech.

Aby to obliczyć, musisz znać dwa punkty linii, których współrzędne są (x x₁,I₁) i (x₂,I₂). Pomiędzy obiema punktami rysowany jest segment, który należy do linii, a następnie segmenty reprezentujące odległość między x są rysowane₁ i x₂, i między i₁ i i₂, jak na dolnej figurze.

Rysunek 1. Nachylenie linii jest styczna kąt θ. Źródło: Wikimedia Commons.

Trzy segmenty stanowią prawy trójkąt, którego nogi są: δx = x₂ - X₁  i Δy = i₂ - I₁. Odpowiadają odpowiednio do poziomego przemieszczenia i kolejnego pionowego.

Teraz zdefiniowano iloraz, zwany styczną kąta θ i skrócone TG θ, co jest dokładnie nachyleniem M linii:

M = tg θ = δY / δx

Zauważ, że dla linii kąt ten pozostaje stały, niezależnie od punktów pobranych w celu obliczenia jego stycznej. W każdym razie ta wartość oferuje nam miarę tego, jak jest to linia.

Dzięki współrzędnym wybranych punktów wzór nachylenia pozostaje:

M = (y - y₁ ) / (X₂ - X₁)

[TOC]

Reprezentacja graficzna

Poniżej mamy kilka sytuacji, w których istotna jest koncepcja nachylenia. Jego wartość można łatwo obliczyć, mierząc odpowiednie przemieszczenie pionowe i poziome, a następnie dokonanie ilorazu wskazanego na początku.

To daje nam wyobrażenie o zboczu lub upadku jakiejś konstrukcji, takiej jak rampa, dach lub droga:

Może ci służyć: losowe pobieranie próbek: metodologia, zalety, wady, przykłady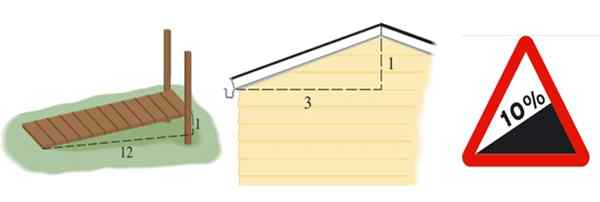 Rysunek 2. Od lewej do prawej zbocza rampy, dachu i nachylenia drogi, te ostatnie wyrażone w procentowym procencie. Źródło: Stewart, J. Precáculculo i Wikimedia Commons (właściwy obraz).

Nachylenie rampy pokazanej na ryc. 2 po lewej wynosi m = 1/12, dach to m = 1/3, a droga jest wyrażana w procentach. 10 % procent oznacza, że ​​na każde 100 metrów, które postępują w poziomie, zarabiają 10 metrów:

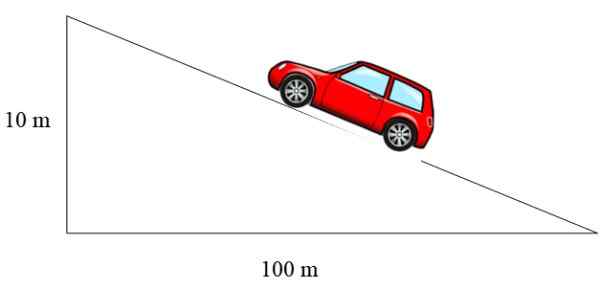Rysunek 3. Pojazd wznosi się przez nachylenie, którego nachylenie wynosi 10%. Źródło: f. Zapata.

W takim przypadku nachylenie wynosi 10/100 = 0.1, który wyrażał się jako odsetek wynosi 10%.

Rodzaje nachylenia

Nachylenie linii może być dodatnie, ujemne lub zerowe. Na przykład linia pokazana na rycinie 1 ma dodatnie nachylenie. Doceniamy to natychmiast, ponieważ widzimy, że linia jest „podniesiona”, jeśli zobaczymy ją od lewej do prawej.

Jeśli linia schodzi, widząc ją od lewej do prawej, jego nachylenie jest ujemne. A kiedy linia jest pozioma, jej nachylenie jest zerowe.

Wreszcie, w przypadku linii pionowych nachylenie nie jest zdefiniowane.

Reprezentacja graficzna każdego typu znajduje się poniżej:

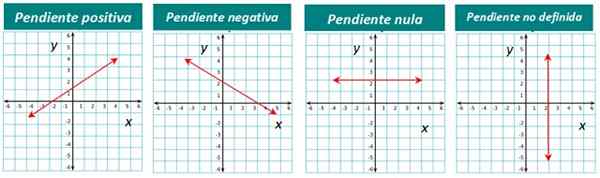Rysunek 4. Linie zgodnie z twoim nachyleniem. Źródło: f. Zapata.

W jaki sposób nachylenie obliczane jest linia?

Obliczanie nachylenia jest bardzo proste, wystarczy znaleźć przemieszczenie pionowe i przemieszczenie poziome, a następnie uczynić iloraz między nimi.

Kiedy masz rysunek linii w płaszczyźnie kartezjańskim, te przemieszczenia wybierają dowolne dwa punkty linii P₁ I p₂, określanie ich współrzędnych i zastosowanie definicji podanej na początku:

Może ci służyć: co reprezentuje długość przemieszczenia sześciokąta

M = (y - y₁ ) / (X₂ - X₁ )

Ponieważ wartość nachylenia jest niezależna od wyboru p₁ I p₂ , Zamierzamy wybrać punkt P współrzędnych (x, y), który należy do linii, której współrzędne nie są znane, a kolejny punkt p₁ których współrzędne to: (x₁,I₁).

Nachylenie to:

M = (y - y₁) / (x - x₁)

Możemy oczyścić I:

i i₁ = m (x - x₁)

Teraz przypuśćmy, że punkt p₁ Jest to przecięcie linii z osą pionową współrzędnych (0, b). Zastępując to w poprzednim równaniu:

i - b = m (x - 0) → y = mx + b

To wyrażenie jest znane jako równanie linii w postaci Oczekiwanie - skrzyżowanie, Ponieważ linia jest jednoznacznie określona, ​​gdy znane są jej nachylenie i przecięcie z osi pionowej.

Znajomość tylko nachylenia nie wystarcza, aby scharakteryzować linię w samolocie, ponieważ nieskończona prosta może mieć to samo nachylenie, co oznacza, że ​​są one równoległe, ale przejdź przez inne punkty.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Znajdź nachylenie linii pokazanej na poniższym rysunku:

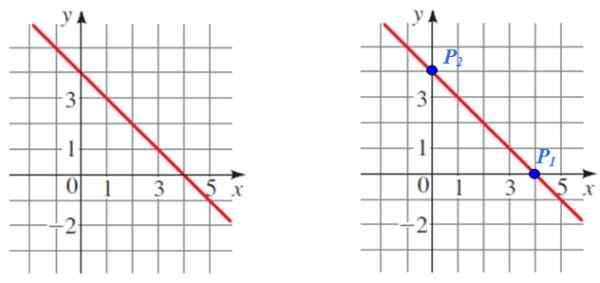Rysunek 5. Przez wykres linii są wybrane dwa punkty w celu obliczenia jej nachylenia. Źródło: f. Zapata.

Rozwiązanie

P₁ I p₂ Są to dwa łatwe punkty, które będą służyć do obliczeń, zauważa również, że są to odpowiednie skrzyżowania z osi współrzędnych.

Współrzędne każdego punktu to:

P₁ (4.0) i P₂ (0,4)

Zastępując równanie nachylenia:

M = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

Nachylenie jest ujemne, czego oczekiwano po obserwowaniu grafiki.

Może ci służyć: liczby złożone: właściwości, przykłady, operacje

- Ćwiczenie 2

Znajdź równanie linii, które przechodzi przez punkt (1, -6) i jest równolegle do linii y = 2x - 3.

Rozwiązanie

Nachylenie poszukiwanej linii musi być takie samo jak w przypadku y = 2x - 3, ponieważ są one równoległe. W tej linii nachylenie wynosi m = 2, dlatego ten, którego szukamy, ma formę:

i i₁ = 2 (x - x₁)

Teraz wymieniamy punkt, przez który przechodzi nasza linia: x₁ = 1 i₁ = -6.

i - (-6) = 2 (x - 1)

Dlatego y = 2x - 2 - 6 → y = 2x - 8

Przykłady

Dwie ilości mogą być powiązane w taki sposób, że Twój wykres jest linią prostą. W takim przypadku mówi się, że kwoty mają zależność liniową, a nachylenie linii można interpretować jako przyczynę zmiany jednej zmiennej na drugą.

Przykład 1

Załóżmy, że basen jest wypełniony wodą do wskaźnik stały w czasie. Oczywiście, im więcej czasu mija, tym więcej wody jest przechowywana. Cóż, szybkość wypełniania puli jest dokładnie nachyleniem linii, która odnosi głośność do czasu:

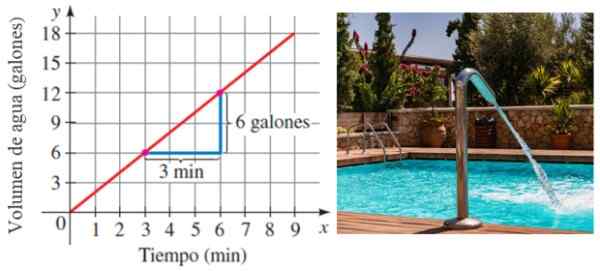Rysunek 6. Stok jako powód do zmiany. Źródło: Stewart, J./Pxfuel.

W tym przykładzie basen jest wypełniony w tempie 6/3 galonów na minutę lub 2 galony/minutę.

Przykład 2

Kiedy telefon komórkowy porusza się w linii prostej ze stałą prędkością, nachylenie wykresu położenia zależy od czasu. Wykres pokazuje telefon komórkowy z dodatnią prędkością, co oznacza, że ​​odchodzi od pochodzenia.

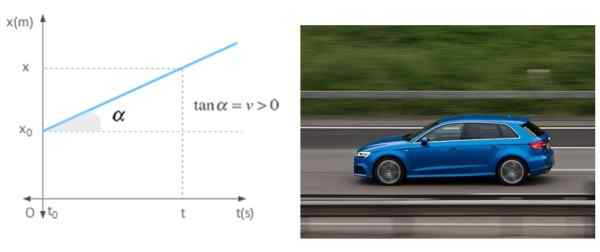Rysunek 7. Nachylenie wykresu w porównaniu z czasem jest prędkość telefonu komórkowego w jednolitym ruchu prostoliniowym. Źródło: Wikimedia Commons/Pixabay.

Bibliografia

1. Alvarez, J. Zbocze drogi. Odzyskany z: Geogebra.Jest.
2. Carena, m. 2019. Podręcznik matematyki przednicznicy. National University of the Coast.
3. Hoffman, J. Wybór problemów z matematyką. Tom 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
6. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.