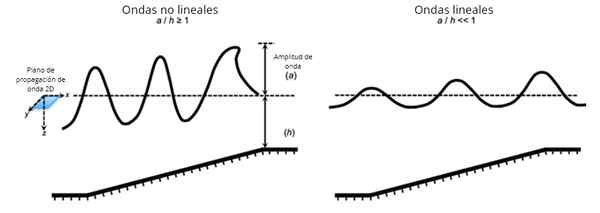
Koncepcja fal liniowych, cechy, przykłady

 Fale liniowe Są to te, w których ma zastosowanie zasadę superpozycji, to znaczy, w których kształt fali i jego ewolucja czasoprzestrzenna można osiągnąć jako sumę podstawowych rozwiązań, na przykład typu harmonicznego. Nie wszystkie fale spełniają zasadę superpozycji, która nie jest zgodna z nią, nazywa się falami nieliniowymi.

„Liniowa” denominacja wynika z faktu, że fale liniowe zawsze spełniają równanie różniczkowe w częściowych pochodnych, w których wszystkie terminy obejmujące zmienną zależną lub jej pochodne są podniesione do pierwszej mocy.

Fale widoczne w odległości są falami liniowymi, jednak przestraszone fale pierwszego planu są niewidalne. Źródło: Pixabay.

Z drugiej strony fale nieliniowe spełniają równania falowe, które mają kwadratowe lub wyższe stopnie w zmiennej zależnej lub w ich pochodnych.

Czasami jest zdezorientowane fale liniowe z falami podłużnymi, w których wibracje występują w tym samym kierunku propagacji, takie jak fale dźwiękowe.

Ale fale podłużne, a także poprzeczne, mogą z kolei być liniowe lub nieliniowe, w zależności od innych czynników, amplitudy początkowego zaburzenia i środowiska, w którym się rozprzestrzeniają.

Zasadniczo zdarza się, że gdy początkowe zaburzenia ma niewielką amplitudę, równanie opisujące propagację fali jest typu liniowego lub może być wyznaczane przez niektóre podejścia, chociaż nie zawsze tak jest.

[TOC]

Równanie różniczkowe w falach liniowych

W medium liniowym ograniczona forma przebiegu w przestrzeni i czasie może być reprezentowana przez sumę funkcji fali zatokowej lub cosinusowej o różnych częstotliwościach i długościach fali za pomocą serii Fouriera. 

Fale liniowe zawsze mają równanie różniczkowe powiązanego typu liniowego, którego rozwiązanie reprezentuje przewidywanie zakłóceń w tylnych momentach początkowego zakłócenia zlokalizowanego przestrzennie na początkowym początkowym natychmiastowym.

Klasyczne równanie fali liniowej, w jednym wymiarze przestrzennym, którego roztworami są fale liniowe to:

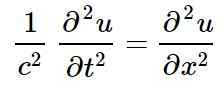
W poprzednim równaniu Lub reprezentuje zakłócenie określonej ilości fizycznej w pozycji X I w tej chwili T, to jest do powiedzenia Lub Jest to funkcja X I T:

Może ci służyć: jakie są wektory koplanares? (Z rozwiązanymi ćwiczeniami)

u = u (x, t)

Na przykład, jeśli jest to fala dźwiękowa w powietrzu, Lub Może reprezentować zmienność ciśnienia w odniesieniu do jej wartości bez zakłócania.

W przypadku fali elektromagnetycznej lub reprezentuje pole elektryczne lub pola magnetyczne oscylujące prostopadle do kierunku propagacji.

W przypadku napiętej liny, Lub reprezentuje przemieszczenie krzyżowe w odniesieniu do równowagi równowagi liny, jak pokazano na poniższym rysunku:

Kształt fali w danej chwili, w przypadku fal liniowych ta postać jest nakładaniem się fal sinusoidalnych o różnych częstotliwościach i długościach fal. Źródło: f. Zapata.

Rozwiązania równań różniczkowych

Jeśli masz dwa lub więcej roztworów liniowego równania różniczkowego, każde rozwiązanie pomnożone przez stałą będzie rozwiązaniem i będzie również ich sumą. 

W przeciwieństwie do równań nieliniowych, równania falowe przyznają się do roztworów harmonicznych typu: 

Lub₁= A⋅sen (k⋅x - ω⋅t) I Lub₂= A⋅sen (k⋅x + ω⋅t) 

Można to zweryfikować przez proste podstawienie w równaniu fali liniowej.

Pierwsze rozwiązanie reprezentuje fala postępująca, która rozwija się po prawej stronie, a druga po lewej stronie C = Ω/k.

Rozwiązania harmoniczne są charakterystyczne dla równań fali liniowej.

Z drugiej strony, liniowa kombinacja dwóch roztworów harmonicznych jest również rozwiązaniem równania fali liniowej, na przykład:

u = a₁ CO (k₁⋅x - ω₁⋅t) + a₂ zlew₂⋅x - ω₂⋅t) jest rozwiązaniem.

Najbardziej istotną cechą fal liniowych jest to, że każda forma fali, jakkolwiek złożona, można uzyskać przez sumę prostych fal harmonicznych w piersi i cosinus:

u (x, t) = a₀ + ∑_N DO_N CO (k_N⋅x - ω_N⋅t) + ∑_M B_M zlew_M⋅x - ω_M⋅t).

Dyspersyjne i nie wystrzeliwane fale liniowe

W klasycznym równaniu fali liniowej, C reprezentuje prędkość propagacji impulsu.

Fale nie wystrzeliwane

W przypadkach, w których C Jest to stała wartość, na przykład fale elektromagnetyczne w pustce, a następnie impuls w początkowym momencie t = 0 Kształt f (x) Rozprzestrzenia się według:

u (x, t) = f (x - c⋅t)

Bez cierpienia żadnych zniekształceń. Kiedy tak się dzieje, mówi się, że medium nie jest projektowane.

Fale dyspersyjne

Jednak w pożywce dyspersyjnej prędkość propagacji C może zależeć od długości fali λ, to znaczy: c = c (λ).

Może ci służyć: równanie ciągłości

Fale elektromagnetyczne są dyspersyjne podczas podróży przez medium materialne. Również fale powierzchniowe wody przemieszczają się z inną prędkością w zależności od głębokości wody.

Prędkość, z jaką propaguje się fala harmoniczna A⋅Sen (k⋅x - ω⋅t) Jest Ω/k = c a prędkość fazowa jest nazywana. Jeśli medium jest dyspersyjne, to C Jest to funkcja liczby fali k: C = C (k), Gdzie k Jest to związane z długością fali za pomocą K = 2π/λ.

Relacje z dyspersją

Zależność między częstotliwością a długością fali nazywana jest Współczynnik dyspersji, to wyrażone w kategoriach częstotliwości kątowej Ω i numer fali k Jest: Ω = c (k) ⋅K.

Niektóre cechy relacji dyspersji fal liniowych są następujące:

W falach, w których długość fali (odległość między grzbietami) jest znacznie większa niż głębokość H, Ale że jego szerokość jest znacznie mniejsza niż głębokość, jaką jest związek dyspersji:

Ω = √ (gh) ⋅K

Stamtąd stwierdzono, że rozprzestrzeniły się z stałą prędkością √ (GH) (Non -Dipersive Połowa).

Ale fale na bardzo głębokich wodach są dyspersyjne, ponieważ ich stosunek dyspersji wynosi:

ω = √ (g/k) ⋅K

Oznacza to tę szybkość fazową Ω/k Jest zmienna i zależy od liczby fali, a zatem od długości fali fali.

Prędkość grupy

Jeśli dwie harmoniczne fale liniowe pokrywają się, ale postępują z różnych prędkości.

Prędkość grupy v_G Jest zdefiniowany jako pochodna częstotliwości w odniesieniu do liczby fali w stosunku dyspersji: v_G = Ω '(k).

Poniższy rysunek pokazuje nakładanie się lub sumę dwóch fal harmonicznych Lub₁= A⋅sen (k₁⋅x - ω₁⋅t) I Lub₂= A⋅sen (k₂⋅x - ω₂⋅t) że podróżują z różnymi prędkościami v₁= Ω₁/k₁ I v₂= Ω₂/k₂. Zwróć uwagę, jak prędkość grupy różni się od prędkości fazowej, w tym przypadku prędkość grupy jest ∆ω/∆k.

Może ci służyć: magnetyczne właściwości materiałów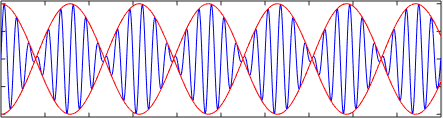Fala liniowa (niebieska) w podłożu dyspersyjnym. Czerwona krzywa została dodana, aby podkreślić, że prędkość grupy różni się od prędkości propagacji

W zależności od współczynnika dyspersji prędkość fazowa i prędkość grupy, w przeciwnych kierunkach, mogą nawet mieć przeciwne kierunki.

Przykłady fal liniowych

Fale elektromagnetyczne

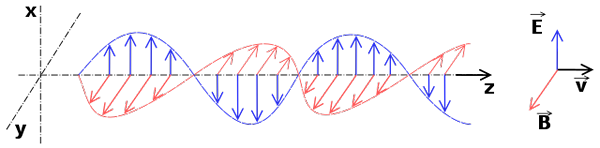fale elektromagnetyczne tworzące promieniowanie elektromagnetyczne

Fale elektromagnetyczne to fale liniowe. Jego równanie falowe wywnioskowane jest z równań elektromagnetyzmu (równania Maxwella), które są również liniowe.

Równanie Schrödingera

Jest to równanie, które opisuje dynamikę cząstek w skali atomowej, w której istotne są charakterystyki pofalowane, na przykład przypadek elektronów w atomie.

Następnie „fala elektronowa” lub fala, jak się nazywa, jest falą liniową.

Fale w głębokiej wodzie

Fale liniowe są również te, w których amplituda jest znacznie niższa niż długość fali i długość fali znacznie większa niż głębokość. Fale w głębokiej wodzie podążają za teorią liniową (znaną jako teoria pofalowana Airy).

Jednak fala, która zbliża się do brzegu i tworzy charakterystyczny grzebień, który jest zwinięty (i który Surfers Loves) to fala nieliniowa.

Dźwięk

Ponieważ dźwięk jest niewielkim zaburzeniem ciśnienia atmosferycznego, jest uważane za falę liniową. Jednak fala uderzeniowa eksplozji lub frontu falowego płaszczyzny naddźwiękowej są typowymi przykładami fal nieliniowych.

Fale na napiętej linie

Fale rozprzestrzeniające się przez napiętą linę są liniowe, pod warunkiem, że początkowa pulsacja jest niewielka, to znaczy elastyczna granica liny nie jest przekraczana.

Fale liniowe na strunach są odzwierciedlone na ich końcach i nakładanie się, co daje stacjonarne fale lub tryby wibracyjne, które nadają tonom harmoniczne i subarmoniczne charakterystyczne dla instrumentów strunowych.

Bibliografia

1. Griffiths G i Schiesser w. Fale liniowe i nieliniowe. Odzyskane z: Sholarpedia.org.
2. Whitham g.B. (1999) „Fale liniowe i nieliniowe”. Wiley. 
3. Wikipedia. Fale nieliniowe. Odzyskane z: jest.Wikipedia.com
4. Wikipedia. Nieliniowy akustyczny. Źródło: w:.Wikipedia.com
5. Wikipedia. Fale. Źródło: w:.Wikipedia.com
6. Wikiwaves. Fale nieliniowe. Odzyskane z: Wikiwaves.org