Właściwości serii Fibonacciego, relacje naturalne, zastosowania

O Serie Sukcesja Fibonacciego jest sekwencją liczb, która jest uzyskiwana przez rozpoczęcie od 0 i 1, kontynuuje ich sumę: 0 + 1 = 1, a następnie suma dwóch poprzednich: 1 + 1 = 2 i tak dalej.

Zgodnie z tą procedurą uzyskane są pozostałe terminy, zobaczmy: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13…

Pierwsza liczba serii Fibonacci

Procedura jest powtarzana tyle razy, ile chcesz. W ten sposób sukcesja Fibonacciego nabiera formę: 0, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Liczby, które to sprawiają, są wywoływane Liczby Fibonacci.

[TOC]

Historia

Sukcesja Fibonacciego nazywa się włoskim matematykiem, który mieszkał w średniowieczu: Leonardo de Pisa, znany również jako Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo spędził dzieciństwo w Afryce Północnej i podróżował po Morzu Śródziemnym, gdzie znał indo -arabiczny system liczby i był z niego zachwycony. Prawdopodobnie arabscy ​​nauczyciele Leonardo nauczyli go o sukcesji, która była już znana przez hinduskich matematyków.

Następnie, gdy wracając do PISA Fibonacci, napisał książkę zatytułowaną Liber Abaci (Księga Abacusa), gdzie oprócz podkreślenia zalet liczb indo -arabicznych w obliczu rzymskiej liczby i wprowadzenia 0, podniósł problem z reprodukcją królików.

A rozwiązaniem tego problemu jest dokładnie liczba sukcesji Fibonacciego.

Leonardo de Pisa nie otrzymał utworzenia sukcesji; Wspomniał o tym tylko w swojej książce jako ciekawość, która zwróciła uwagę wielu uczonych, którzy podążyli za nim. Wśród nich był dziewiętnastowieczny francuski matematyk Edouard Lucas, który podczas studiowania sukcesji ochrzcił ją imieniem średniowiecznego mędrca, który przekazał to na Zachodzie.

Problem królików Fibonacci

Problem mówi: Kilka królików żyje wiecznie, co w wieku dwóch miesięcy jest żyzne. Po osiągnięciu dojrzałości mają one kilka dzieci o różnej płci co miesiąc, które również zajmują dwa miesiące i mają miesięczne kilka królików.

Może ci służyć: de Morgan Laws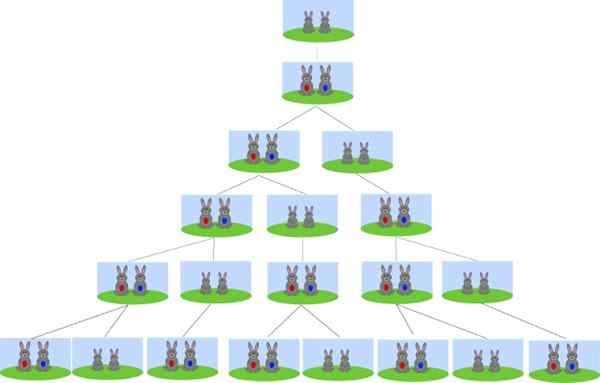Pochodzenie sukcesji Fibonacciego jest problem reprodukcji królików. Źródło: Wikimedia Commons.

Zaczynając od kilku nowonarodzonych królików, ile par będzie za miesiąc? Ile par królików będzie po 2, 3 i 4 miesiącach? I ile będzie po 6 miesiącach?

Odpowiedź jest w liczbach Fibonacciego. Po 1 miesiącu jest 1 para królików, oryginalna para, ponieważ rozmnażają się dopiero po 2 miesiącach.

Po 2 miesiącach są 2 pary królików: oryginalna para i ich pierwszy ściółka.

Po 3 miesiącach będziemy mieli 3 pary, w tym oryginalna para, ich pierwszy ściółka i nowy.

Po osiągnięciu czwartego miesiąca będziemy mieć pierwotną parę, pierwszą ściółkę, która z kolei ma swoje pierwsze dzieci, miot trzeciego miesiąca i nowy miot. W sumie 5 par królików.

Ale są to liczba sekwencji Fibonacciego, dlatego po 6 miesiącach będzie 13 par królików, ponieważ każdego miesiąca dodawane są pary z poprzednich dwóch miesięcy.

Właściwości serii Fibonacciego

Oto kilka interesujących właściwości sukcesji Fibonacciego.

Właściwość 1

Rekurencyjna formuła znalezienia warunków sukcesji jest:

Do_N+1 = a_N + Do_N-1  Dla n większych lub równych 2.

Gdzie n = 2, 3, 4,… to znaczy znaleźć siódmy termin a₇, Robimy n = 6, aby 6+1 = 7. Musimy znać warunki₅  już₆, listy, która pojawia się we wstępie do₅ = 5 i a₆ = 8, więc do₇ = 5+8 = 13.

Właściwość 2

Jeśli dwa terminy, które chcemy znaleźć, nie są znane, możemy użyć następującej formuły:

Może ci służyć: Tesseldos: Charakterystyka, typy (regularne, nieregularne), przykłady

Właściwość 3

Liczby a_N już_N+1 Czy  Coprimos, to znaczy są kuzynami ze sobą, co oznacza, że ​​nie mają wspólnych wspólnych czynników.

Właściwość 4

Bardzo interesująca właściwość jest iloraz między warunkami_2n już_N, co jest warte 1, gdy n = 1. To jest do powiedzenia:

Do₂ / Do₁ = 1

Możemy to łatwo sprawdzić z listą liczb Fibonacciego.

Z drugiej strony, jeśli n ≠ 1, to iloraz jest:

Do_2n / Do_N = a_N  + 2_N-1

Na przykład, jeśli n = 3, to a _2n = a₆ = 8 i₃ = 2. No więc:

8/2 = 2 + 2. Do₂ = 2 + 2. 1

Rzeczywiście: 8/2 = 4 i 2 + (2.1) = 4. Można zweryfikować, że dowolna wartość N jest spełniona.

Własność 5

Stosunek r_N = a_N+1 / Do_{N ,} Kiedy n staje się wielki, zbiega się do Złoty rozum albo Aurea proporcja, Irracjonalna liczba, która często powstaje w naturze, podana przez:

Naturalne relacje sukcesji Fibonacciego

Sukcesja Fibonacciego w roślinach

Objawy sukcesji Fibonacciego obfitują w królestwo roślin

Gałęzie niektórych drzew wychodzą co roku według sukcesji Fibonacciego. W pierwszym roku pnia rośnie bez rzucania żadnego oddziału, po roku produkuje jeden i tak w każdym roku. Z kolei każda gałąź może rzucić kolejną nowe po roku, tak jak króliki się rozmnażają.

Centrum Słoneczników zawiera nasiona ułożone w logarytmicznych wiązkach spiralnych, w obu sensie, których ilości odpowiadają dwóch kolejnych liczb Fibonacci.

Liczby Fibonacciego są obecne w liczbie płatków słonecznika i kwiatów margaritowych, a także w licznych wzorach, w których rośliny mają liście.

Może ci służyć: zmienna porządkowa

Eksperci twierdzą, że w ten sposób rośliny optymalizują przestrzeń do liści i kwiatów, aby mieć optymalny wzrost.

Z centralnym punktem jako miejscem początkowym, struktury te rosną i otrzymują światło słoneczne, dlatego nowe liście i płatki muszą pokryć tak mało, jak to możliwe. A najlepszym sposobem na osiągnięcie tego jest przyjęcie wzorca wzrostu pod względem sekwencji Fibonacciego.

Sukcesja Fibonacciego u zwierząt

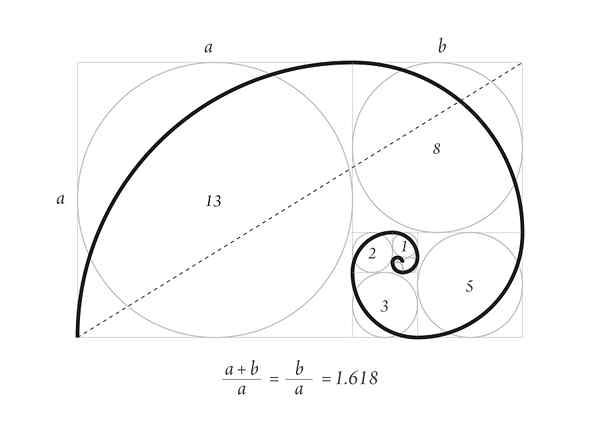Spirala Durero z pierwszą liczbą sukcesji Fibonacciego

Trwała spirala górnego obrazu jest częścią wzoru wzrostu skorupek u zwierząt morskich i rogów niektórych przeżuwaczy.

Zacznij od dwóch kwadratów 1, jeden na drugim, a następnie kwadrat z boku 2 obok niego, który stanowi prostokąt strony 3, którego boki mają złoty proporcja.

Poniżej znajduje się kwadrat z boku 3 i po lewej stronie kwadratu z boku 5. Powyżej znajduje się kwadrat z boku 8 i po prawej stronie kwadrat z boku 13. To jest pierwsza liczba sukcesji.

Wreszcie spirala jest narysowana przez dotykanie punktów narożników kwadratów, jak widać na rysunku.

Aplikacje

Sukcesja Fibonacciego jest stosowana w różnych dziedzinach:

-W sztuce Złota proporcja związana z sukcesją Fibonacciego pojawia się w ludziach i rzeczach reprezentowanych przez wielkich artystów, takich jak Leonardo da Vinci, Miguel Ángel i Alberto Durero.

-Proporcje partnera w Atenach również reagują na numer złota.

-W kompozycjach Mozarta, Beethoven, Schubert i Debussy.

-Aby zaprojektować przedmioty, których proporcje wyglądają harmonijnie dla ludzkich oczu, takich jak karty kredytowe, kontenery, flagi.

-Na giełdzie jest wykorzystywany do przewidywania, jakie ceny zwraca jej trend.

Bibliografia

1. Sukcesja Fibonacciego. Odzyskane z: blogeducastur.Jest.
2. Stewart, J. 2007. Przedłużanie. 5. Wydanie. Cengage Learning.
3. Vargas, m. Zastosowania sukcesji Fibonacciego. Odzyskane od: Matesup.Cl.
4. Wikipedia. Numer Fibonacciego. Źródło: w:.Wikipedia.org.