Wyimaginowane właściwości liczb, aplikacje, przykłady

Wyobrażone liczby Są to te, które podają rozwiązanie równaniu, w którym nieznany, wysokie kwadratowy, jest równy rzeczywistej liczbie ujemnej. Wyimaginowa jednostka jest I = √ (-1).

W równaniu: z²= - a, z Jest to wyobrażona liczba wyrażona w następujący sposób:

 Z = √ (-a) = i√ (a)

Istnienie Do Pozytywna liczba rzeczywista. Tak A = 1, Więc Z = i, Gdzie Siema jest jednostką wyimaginowaną.

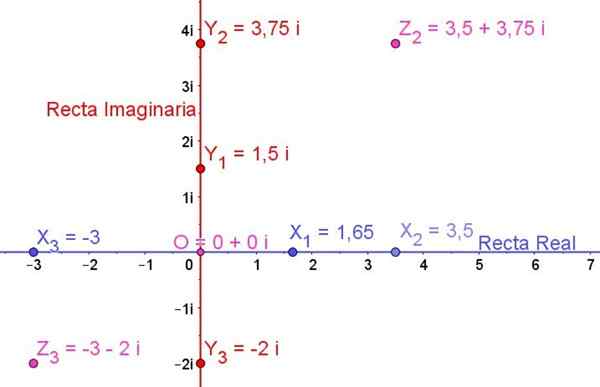Rysunek 1. Złożona płaszczyzna pokazujący niektóre liczby rzeczywiste, niektóre wyobrażone liczby i niektóre złożone liczby. Źródło: f. Zapata.

Ogólnie rzecz biorąc, wyimaginowana liczba Z jest zawsze wyrażana w formie: 

Z = y⋅I

Gdzie I To jest prawdziwa liczba i Siema jest jednostką wyimaginowaną.

A także liczby rzeczywiste są reprezentowane na linii, zwane Prawdziwa prosta, Analogiczne liczby wyimaginowane są reprezentowane na Wyimaginowana prosta.

Wyimaginowana prosta Jest zawsze ortogonalny (forma 90º) do Prawdziwa prosta a dwie linie definiują płaszczyznę kartezjańską zwaną Złożona płaszczyzna.

Rycina 1 pokazuje złożoną płaszczyznę i niektóre liczby rzeczywiste, niektóre wyobrażone liczby, a także niektóre liczby złożone są na niej:

X₁, X₂, X₃ To liczby rzeczywiste

I₁, I₂, I₃ Są to wyimaginowane liczby

Z₂ i z₃ Są to złożone liczby

Liczba lub jest prawdziwym zero i jest także wyimaginowanym zero, dzięki czemu pochodzenie lub jest zerowym kompleksem wyrażonym przez:

0 + 0i 

[TOC]

Nieruchomości

Zestaw wyimaginowanych liczb jest oznaczony przez:

I = …, -3i,…, -2i,… .,-Siema,… .,0i, .. .,Siema,… .,2i, .. .,3i,…

I niektóre operacje dotyczące tego zestawu numerycznego można zdefiniować. Wyimaginowana liczba nie zawsze jest uzyskiwana z tych operacji, więc zobaczymy je z nieco więcej szczegółów:

Suma i odejmowanie wyimaginowanych

Wyimaginowane liczby mogą dodawać i odejmować od siebie nawzajem, w wyniku czego pojawi się nowa liczba wyobraźni. Na przykład:

Może ci służyć: względni kuzyni: co to są, wyjaśnienie, przykłady

 3i + 2i = 5i

4i - 7i = -3i

Wyimaginowany produkt

Kiedy produkt wyimaginowanej liczby z inną jest, wynikiem jest liczba rzeczywista. Wykonajmy następującą operację, aby sprawdzić:

2i x 3i = 6 x i² = 6 x (√ (-1))² = 6 x (-1) = -6.

I jak widzimy, -6 jest liczbą rzeczywistą, chociaż uzyskano ją przez pomnożenie dwóch czystych liczb wyimaginowanych.

Produkt liczby rzeczywistych dla kolejnego wyobrażonego

Jeśli liczba rzeczywista zostanie pomnożona przez I, wynikiem będzie liczba wyobraźni, która odpowiada obrotowi 90 stopni.

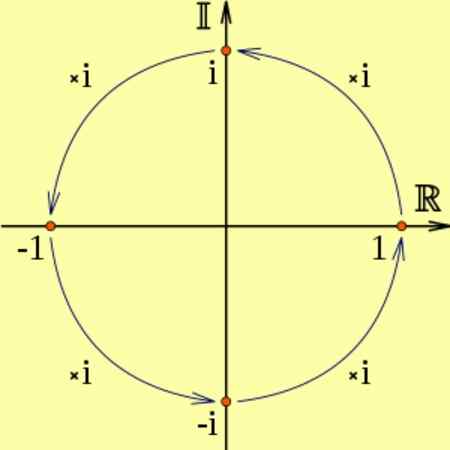
I czy to ja² odpowiada dwóm kolejnym obrotom 90 stopni, co jest równoważne z pomnożeniem przez -1, to znaczy i² = -1. Można to zobaczyć na poniższym schemacie:

Rysunek 2. Mnożenie przez jednostkę wyobrażoną i odpowiada obrotom 90º. Źródło: Wikimedia Commons.

Na przykład:

-3 x 5i = -15i

-3 x i = -3i.

Nasilenie wyimaginowanego

Można zdefiniować wzmocnienie wyimaginowanej liczby do całego wykładnika:

Siema¹ = i

Siema² = i x i = √ (-1) x √ (-1) = -1

Siema³ = i x i² = -I

Siema⁴ = i² x i² = -1 x -1 = 1

Siema⁵ = i x i⁴ = i

Ogólnie musisz Siema^N = i^(n mod 4), Gdzie Mod Jest to pozostałość podziału między N I 4.

Można również wykonać nasilenie negatywnych liczb całkowitych:

Siema^-1 = 1 / i¹ = i / (i x i¹) = I / (i²) = I / (-1) = -i

Siema-² = 1 / i² = 1/ (-1) = -1

Siema-³= 1 / i³ = 1 / (-i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Ogólnie rzecz biorąc, wyobrażona liczba b⋅i podwyższona do mocy n to:

(B⋅i) i^N = b^N Siema^N = b^N I^(n Mod 4)

Niektóre przykłady są następujące:

(5 i)¹² = 5¹² Siema¹² = 5¹² Siema⁰ = 5¹² x 1 = 244140625

(5 i)^jedenaście = 5^jedenaście Siema^jedenaście = 5^jedenaście Siema³ = 5^jedenaście x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ Siema¹⁰ = 2¹⁰ Siema² = 1024 x (-1) = -1024

Suma rzeczywistej liczby i jedno wyobrażone

Gdy liczba rzeczywista jest dodawana z wyimaginowaną, wynik nie jest ani rzeczywisty, ani wyobrażony, jest to nowy rodzaj nazywanej liczby Liczba zespolona.

Na przykład, jeśli x = 3,5 i y = 3,75i, wynik jest liczbą złożoną:

Może ci służyć: minimalne kwadraty

Z = x + y = 3,5 + 3,75 i

Zwróć uwagę, że rzeczywistych i wyimaginowanych części nie można pogrupować w sumie, więc liczba złożona zawsze będzie miała prawdziwą część i inną część wyobraźni.

Ta operacja rozszerza zestaw liczb rzeczywistych na najszerszą z liczb złożonych.

Aplikacje

Nazwa wyobrażonych liczb została zaproponowana przez francuski matematyk René Descartes (1596-1650) jako kpina lub spór z ich propozycją złożoną przez włoskiego matematyka Raffaelle Century Bombelli.

Inni wielcy matematycy, tacy jak Euler i Leibniz, poparli Kartezjusza w tej nieporozumieniu i nazwali wyobrażone liczby jako liczby płazów, które były dyskutowane między byciem a nicość.

Nazwa wyimaginowanych liczb jest utrzymywana dzisiaj, ale jej istnienie i znaczenie są bardzo realne i namacalne, ponieważ pojawiają się naturalnie w wielu dziedzinach fizyki, takich jak:

-Teoria względności.

-W elektromagnetyzmie.

-Mechanika kwantowa.

Ćwiczenia z wyimaginowanymi liczbami

- Ćwiczenie 1

Znajdź rozwiązania następującego równania:

z² + 16 = 0

Rozwiązanie

z² = -16

Mając pierwiastek kwadratowy w obu członkach:

√ (z² ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Innymi słowy, rozwiązania pierwotnego równania to:

Z = +4i lub z = -4i.

- Ćwiczenie 2

Znajdź wynik podniesienia wyimaginowanej jednostki do zasilania 5 minus odejmowanie Wyimaginowaną jednostkę podwyższoną do mocy -5.

Rozwiązanie

Siema⁵ - Siema-⁵ = i⁵ - 1/i⁵ = i - 1/i = i - (i)/(i x i) = i - i/( - 1) = i + i = 2i

- Ćwiczenie 3

Znajdź wynik następującej operacji:

(3i)³ + 9i 

Rozwiązanie

3³ Siema³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Ćwiczenie 4

Znajdź rozwiązania następującego równania kwadratowego:

Może ci służyć: twierdzenie o istnieniu i wyjątkowości: demonstracja, przykłady i ćwiczenia

(-2x)² + 2 = 0

Rozwiązanie

Równanie jest przełożone w następujący sposób:

(-2x)² = -2

Następnie weź pierwiastek kwadratowy u obu członków

√ ((-2x)²) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Następnie X jest ostatecznie uzyskane:

x = ± √2 / 2 i

Oznacza to, że istnieją dwa możliwe rozwiązania:

x = (√2 / 2) i

Lub to inne:

x = - (√2 / 2) i

- Ćwiczenie 5

Znajdź wartość Z zdefiniowaną przez:

Z = √ (-9) √ (-4) + 7

Rozwiązanie

Wiemy, że pierwiastek kwadratowy ujemnej liczby rzeczywistej jest liczbą wyobraźni, na przykład √ (-9) jest równy √ (9) x √ (-1) = 3i.

Z drugiej strony √ (-4) jest równe √ (4) x √ (-1) = 2i.

Tak, aby oryginalne równanie można było zastąpić:

3i x 2i - 7 = 6 i² - 7 = 6 (-1) -7 = -6 -7 = -13

- Ćwiczenie 6

Znajdź wartość Z wynikającą z następującego podziału dwóch złożonych liczb:

Z = (9 - i²) / (3 + i)

Rozwiązanie

Licznik wyrażenia może uwzględniać przy użyciu następującej właściwości:

Różnica kwadratów jest iloczynem sumy przez różnicę dwumianów bez podniesienia kwadratu.

Więc:

Z = [(3 - i) (3 + i)] / (3 + i)

Powstałe wyrażenie jest następnie uproszczone przez pozostałe

Z = (3 - i)

Bibliografia

1. Earl, r. Liczby zespolone. Odzyskane z: matematyki.wół.AC.Wielka Brytania.
2. Figuera, J. 2000. Matematyka 1st. Urozmaicony. Edycje CO-Bo.
3. Hoffmann, j. 2005. Wybór problemów z matematyką. Publikacje Monfort.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Wyimaginowana liczba. Źródło: w:.Wikipedia.org