Właściwości liczb złożonych, przykłady, operacje

Liczby zespolone Są to zestaw liczbowy, który obejmuje liczby rzeczywiste i wszystkie korzenie wielomianów, w tym równomierne korzenie liczb ujemnych. Te korzenie nie istnieją w zestawie liczb rzeczywistych, ale w liczbach złożonych jest rozwiązaniem.

Złożona liczba składa się z prawdziwej części, a inna nazywana „wyobrażonym”. Prawdziwa część nazywa się Do, Na przykład i wyobrażona część Ib, z Do I B rzeczywiste liczby i „ja” lubię Wyimaginowa jednostka. W ten sposób złożona liczba przyjmuje formularz:

Z = a + ib

Rysunek 1.- Dwumianowa reprezentacja złożonej liczby pod względem części rzeczywistej i części wyobrażonej. Źródło: Pixabay.

Przykładami liczb złożonych to 2 - 3i, -πi, 1 + (1/2) i. Ale zanim z nimi działał, zobaczmy, skąd pochodzi wyimaginowa jednostka Siema, Biorąc pod uwagę to równanie kwadratowe:

X² - 10x + 34 = 0

W którym a = 1, b = -10 i c = 34.

Po zastosowaniu wzoru rozpuszczalnika w celu ustalenia rozwiązania, znajdujemy następujące:

Jak określić wartość √-36? Nie ma liczby rzeczywistych, że kwadrat ma ujemną kwotę. Następnie stwierdzono, że to równanie nie ma prawdziwych rozwiązań.

Możemy jednak to napisać:

√-36 = √-6² = √6² (-1) = 6√-1

Jeśli zdefiniujemy określoną wartość X tak, że:

X² = -1

Więc:

x = ± √-1

A poprzednie równanie miałoby rozwiązanie. Dlatego wyimaginowa jednostka została zdefiniowana jako:

I = √-1

A więc:

√-36 = 6i

Wielu starożytnych matematyków pracowało nad rozwiązaniem podobnych problemów, podkreślając renesans Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) i Raffaele Bombelli (1526-1572).

Wiele lat później René Descartes (1596-1650) nazwał „wyobrażone” do takich ilości, jak √-36 przykładu. Z tego powodu √-1 jest znany jako Wyimaginowa jednostka.

[TOC]

Właściwości liczb złożonych

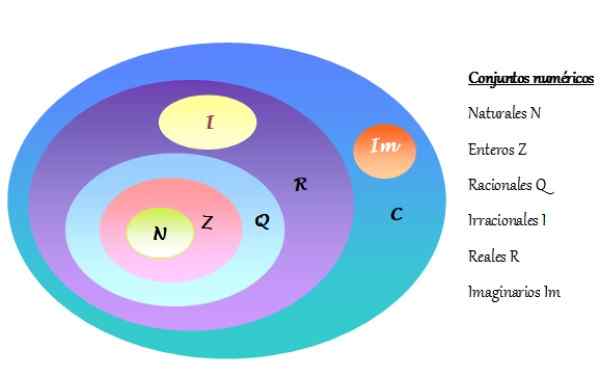
-Zestaw liczb złożonych jest oznaczony jako C i zawiera liczby rzeczywiste R i liczby wyobrażone IM. Zestawy numeryczne są reprezentowane na schemacie Venna, jak pokazano na poniższym rysunku:

Może ci służyć: rozdzielone ćwiczenia czynnikowe Rysunek 2. Diagram Venna zestawów numerycznych. Źródło: f. Zapata.

-Każda złożona liczba składa się z jednej prawdziwej części i drugiej wyobrażonej części.

-Kiedy wyobrażona część liczby złożonej wynosi 0, jest to czysta liczba rzeczywista.

-Jeśli prawdziwą częścią liczby złożonej jest 0, liczba jest czysta wyobrażona.

-Dwie liczby złożone są takie same, jeśli ich odpowiednia część i część wyobrażona są takie same.

-W przypadku liczb złożonych przeprowadzane są znane operacje sum, odejmowania, mnożenia, produktu i wzmocnienia, co skutkuje inną liczbą złożoną.

Reprezentacja liczb złożonych

Liczby złożone mogą być reprezentowane na różne sposoby. Oto główne:

- Forma dwulimiowa

Jest to podana forma na początku, gdzie z to liczba złożona, Do jest prawdziwą częścią, B jest częścią wyimaginowaną i Siema Jest to wyimaginowana jednostka:

Z = a + ib

Lub także:

Z = x + iy

Jednym ze sposobów wykresu liczby złożonej jest przez złożoną płaszczyznę pokazaną na tym rysunku. Wyimaginowana oś jest pionowa, podczas gdy prawdziwa oś jest pozioma i oznacza, że ​​są ponownie.

Liczba złożona z Jest reprezentowany w tej płaszczyźnie jako punkt współrzędnej (X, y) albo (A, B), Tak jak w przypadku punktów prawdziwej płaszczyzny.

Odległość od pochodzenia do punktu Z jest modułem liczby złożonej, oznaczonej jako R, podczas gdy φ jest kątem, który tworzy R Z prawdziwą osą.

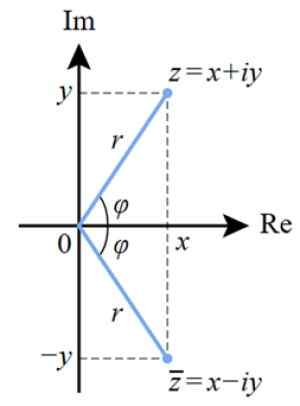Rysunek 3. Reprezentacja liczby złożonej w złożonej płaszczyźnie. Źródło: Wikimedia Commons.

Ta reprezentacja jest ściśle związana z reprezentantami wektorów w prawdziwej płaszczyźnie. Wartość R odpowiada moduł złożonej liczby.

Może ci służyć: Gauss-Seidel Metoda: Objaśnienie, aplikacje, przykłady

- Forma polarna

Forma polarna polega na wyrażaniu liczby złożonej podając wartości R i φ. Jeśli spojrzymy na liczbę, wartość R Odpowiada hipotence prawego trójkąta. Kategorie są warte Do I B, O Cóż X I I.

W formie dwumianowej lub dwumianowej możemy przejść do formy polarnej przez:

R = √x²+I²

Kąt φ Jest to ten, który tworzy segment R z osą poziomą lub osą wyobrażoną. Jest znany jako argument złożonej liczby. Tą drogą:

φ = arctg (y/x)

Argument ma nieskończone wartości, biorąc pod uwagę, że za każdym razem, gdy zwrot jest wart, co jest warte 2π radian, R znów zajmuje tę samą pozycję. W ten sposób ogólnie argument Z, oznaczony arg (z), jest wyrażany w następujący sposób:

Arg (z) = φ + 2kπ

Gdzie K jest całość i służy wskazanie ilości zakrętów: 2, 3, 4 .. . Znak wskazuje znaczenie obrotu, jeżeli czas lub antyhorario.

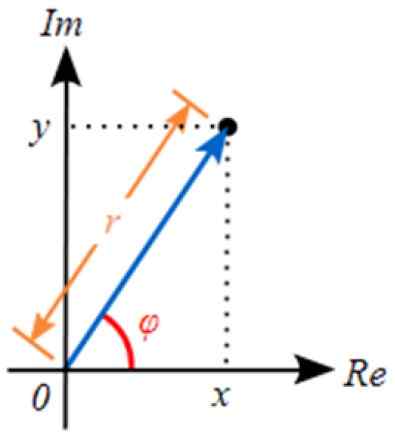Rysunek 4. Polarna reprezentacja złożonej liczby w złożonej płaszczyźnie. Źródło: Wikimedia Commons.

A jeśli chcemy przekazać formę polarną do formy dwumianowej, używamy przyczyn trygonometrycznych. Z poprzedniej figury możemy zobaczyć:

x = r cos φ

y = r sen φ

W ten sposób z = r (cos φ+i sin φ)

To jest skrócone w ten sposób:

Z = r cis φ

Przykłady liczb złożonych

Poniższe liczby złożone są podawane dwuosobowo:

a) 3 + i

b) 4

d) -6i

I te w uporządkowanym momencie obrotowym:

a) (-5, -3)

b) (0, 9)

c) (7.0)

Wreszcie, ta grupa otrzymuje polarne lub trygonometryczne:

a) √2 cis 45º

b) √3 cis 30º

Może ci służyć: rozkład hipergeometryczny: wzory, równania, model

c) 2 cis 315º

Po co oni?

Przydatność liczb złożonych wykracza poza rozdzielczość równania drugiego stopnia pokazanego na początku, ponieważ są one niezbędne w dziedzinie inżynierii i fizyki, szczególnie w:

-Badanie fal elektromagnetycznych

-Alternatywna analiza prądu i napięcia

-Modelowanie wszelkiego rodzaju sygnałów

-Teoria względności, w której czas przyjmuje się jako wyobraźnię.

Operacje o złożonych liczbach

Z liczbami złożonymi możemy wykonywać wszystkie operacje wykonane z rzeczywistością. Niektóre są łatwiejsze, jeśli liczby pojawiają się bezwzględnie, takie jak suma i odejmowanie. Z drugiej strony mnożenie i podział są prostsze, jeśli są przeprowadzane z formą polarną.

Spójrzmy na kilka przykładów:

- Przykład 1

Dodaj z₁ = 2 + 5i i z₂ = -3 -8i

Rozwiązanie

Prawdziwe części są dodawane osobno od części wyimaginowanych:

z₁ + z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Przykład 2

Pomnóż z₁ = 4 cis 45º i Z₂ = 5 cis 120º

Rozwiązanie

Można wykazać, że iloczyn dwóch złożonych liczb w polarnym lub trygonometrycznym jest podany przez:

z₁ . z₂ = r₁.R₂ CIS (φ₁ + φ₂)

Według tego:

z₁ . z₂ = (4 × 5) cis (45 + 120) = 20 cis 165º

Aplikacja

Prostym zastosowaniem liczb złożonych jest znalezienie wszystkich korzeni równania wielomianowego, takiego jak ten pokazany na początku artykułu.

W przypadku równania x² - 10x + 34 = 0, przy zastosowaniu wzoru rozpuszczalnika jest uzyskiwana:

Dlatego rozwiązania to:

X₁ = 5 + 3i

X₂ = 5 - 3i

Bibliografia

1. Earl, r. Liczby zespolone. Odzyskane z: matematyki.wół.AC.Wielka Brytania.
2. Figuera, J. 2000. Matematyka 1st. Urozmaicony. Edycje CO-Bo.
3. Hoffmann, j. 2005. Wybór problemów z matematyką. Publikacje Monfort.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Liczby zespolone. Źródło: w:.Wikipedia.org