Charakterystyczne liczby pierwotne, przykłady, ćwiczenia

liczby pierwsze, nazywane także absolutnymi kuzynami, są te naturalne liczby, które są tylko podzielne ze sobą i 1. W tej kategorii liczby takie jak: 2, 3, 5, 7, 11, 13, 17, 19, 23 i wiele innych pojawiają się w tej kategorii.

Z drugiej strony liczba złożona jest sama podzielna, przez 1 i co najmniej jedna liczba. Mamy na przykład 12, co jest podzielne przez 1, 2, 4, 6 i 12. Zgodnie z konwencją 1 nie jest zawarty na liście liczb pierwszych lub w związkach.

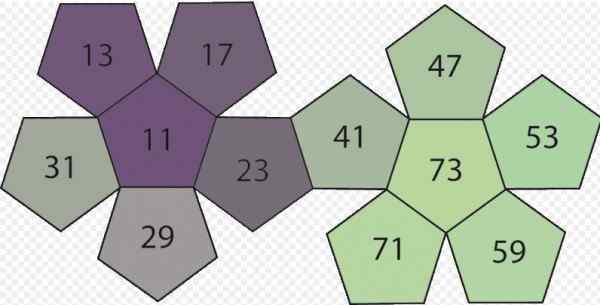
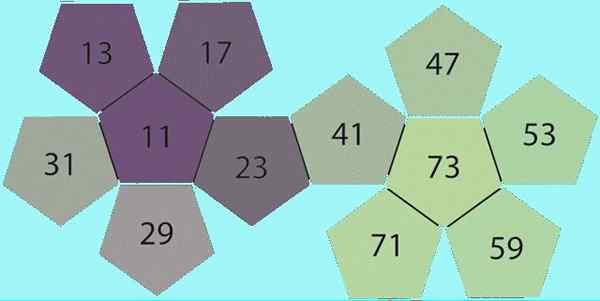Rysunek 1. Niektóre liczby pierwsze. Źródło: Wikimedia Commons.

Znajomość liczb pierwszych pochodzi z czasów zdalnych; Starożytni Egipcjanie już ich poradzili i na pewno byli znani na długo wcześniej.

Liczby te są bardzo ważne, ponieważ każda naturalna liczba może być reprezentowana przez iloczyn liczb pierwszych, będąc tym wyjątkowym reprezentacją, z wyjątkiem kolejności czynników.

Fakt ten jest w pełni ustalony w nazywanym twierdzeniu Podstawowe twierdzenie arytmetyki, które stwierdza, że ​​liczby, które nie są kuzynami, koniecznie składają się z produktów liczbowych.

[TOC]

Charakterystyka liczb pierwszych

Poniżej głównych cech liczb pierwszych:

-Są nieskończone, ponieważ jakkolwiek duża liczba pierwsza zawsze można znaleźć.

-Jeśli liczba pierwsza P nie dzieli dokładnie na inną liczbę Do, To jest wtedy powiedziane P I Do Są ze sobą kuzynami. Kiedy tak się dzieje, jedynym wspólnym dzielnikiem jest 1.

Nie jest to konieczne Do Być absolutnym kuzynem. Na przykład 5 jest kuzynem i chociaż 12 nie jest, obie liczby są ze sobą kuzynami, ponieważ obie mają wspólnego dzielnika na 1.

-Kiedy liczba pierwsza P Podziel moc liczby N, Dzieli również N. Rozważ 100, co jest mocą 10, w szczególności 10². Zdarza się, że 2 dzieli zarówno 100, jak i 10.

-Wszystkie liczby Prime są dziwne, z wyjątkiem 2, dlatego ich ostatnia cyfra to 1, 3, 7 lub 9. 5 nie jest uwzględnione, ponieważ chociaż jest to dziwne i kuzynki, nigdy nie jest to ostateczna liczba kolejnej liczby. W rzeczywistości wszystkie liczby, które kończą się w 5, są ich wielokrotnościami i dlatego nie są kuzynami.

Może ci służyć: centralna symetria: właściwości, przykłady i ćwiczenia

-Tak P To kuzyn i dzielnik produktu dwóch liczb Do.B, Więc P podziel jednego z nich. Na przykład liczba pierwsza 3 dzieli produkt 9 x 11 = 99, ponieważ 3 jest dzielnikiem 9.

Jak wiedzieć, czy liczba to kuzyn

Pierwotność Jest to nazwa nadana jakości bycia kuzynem. Cóż, francuska matematyka Mały twierdzenie Fermata, To mówi:

„Biorąc pod uwagę naturalną liczbę kuzynów P i każda naturalna liczba Do większe niż 0, jest tak spełnione Do^P - Do To wielokrotność P, dopóki P Bądź kuzynem ".

Możemy to potwierdzić za pomocą małych liczb, na przykład przypuszczaj P = 4, Że już wiemy, że to nie jest kuzyn i a = 6:

6⁴ - 6 = 1296 - 6 = 1290

Liczba 1290 nie jest do końca podzielna między 4, dlatego 4 nie jest liczbą pierwszą.

Zróbmy teraz test z p = 5, który jest kuzynem i a = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 jest podzielne między 5, ponieważ dowolna liczba, która kończy się na 0 lub 5. W rzeczywistości 7760/5 = 1554. Ponieważ małe twierdzenie Fermata jest spełnione, możemy upewnić się, że 5 jest liczbą główną.

Test przez twierdzenie jest skuteczny i bezpośredni z niewielkimi liczbami, w których operacja jest łatwa do wykonania, ale co zrobić, jeśli poprosą nas o zapoznanie się z pierwotnością dużej liczby?

W takim przypadku liczba ta jest sukcesywnie podzielona między wszystkie mniejsze liczby pierwotne, aż do dokładnego podziału lub że iloraz jest mniejszy niż dzielnik.

Jeśli jakikolwiek podział jest dokładny, oznacza to, że liczba jest złożona, a jeśli iloraz jest mniejszy niż dzielnik, oznacza to, że liczba ta jest kuzynem. Zatrudnimy to w praktyce w Roku 2.

Sposoby znalezienia liczby pierwszej

Istnieją nieskończone liczby pierwotne i nie ma unikalnej formuły do ​​ich ustalenia. Jednak obserwowanie niektórych liczb pierwszych takich:

Może ci służyć: kąt zerowy: definicja i cechy, przykłady, ćwiczenia

3, 7, 31, 127 ..

Obserwuje się, że są one w postaci 2^N - 1, z n = 2, 3, 5, 7, 9 ... Zapewniamy cię:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Ale nie możemy zapewnić, że ogólnie 2^N - 1 być kuzynem, ponieważ istnieją pewne wartości N dla którego nie działa, na przykład na 4:

2⁴ - 1 = 16 - 1 = 15

A numer 15 nie jest kuzynem, ponieważ kończy się na 5. Jednak jedna z największych znanych liczb pierwszych, znalezionych w obliczeniach komputerowych, znajduje się w formularzu 2^N - 1 z:

N = 57.885.161

Formuła Mersenne Zapewnia nas, że 2^P - 1 jest zawsze kuzynem, tak długo P Bądź też kuzynem. Na przykład 31 jest kuzynem, więc jest pewne, że 2³¹ - 1 Jest to również:

2³¹ - 1 = 2.147.483.647

Jednak formuła umożliwia określenie tylko niektórych liczb pierwszych, nie wszystkie.

Formuła Eulera

Poniższy wielomian pozwala znaleźć liczby pierwszorzędne, o ile N wynosi od 0 do 39:

P (n) = n² + N + 41

Później w sekcji rozwiązywanych ćwiczeń jest przykład jego użycia.

Pokrycie Eratostenes

Eratóstenes był sylwetką i matematyką starożytnej Grecji, która żyła w trzecim wieku.C. Opracował graficzną metodę znalezienia liczb pierwszych, którą możemy zastosować w praktyce z małymi liczbami, nazywa się ekran Eratóstenes (ekran jest jak sitko).

-Liczby są umieszczone w tabeli takiej jak ta pokazana w animacji.

-Wtedy liczby parzyste są oznaczone, z wyjątkiem 2, o których wiemy, że jest kuzynem. Wszystkie inne są tego wielokrotności i dlatego nie są kuzynami.

-Mnożniki 3, 5, 7 i 11 są również oznaczone, wykluczając je wszystkie, ponieważ wiemy, że są kuzynami.

-Mnożniki 4, 6, 8, 9 i 10 są już oznaczone, ponieważ są to związki, a zatem mnożniki dowolnego z wskazanych kuzynów.

Może ci służyć: Historia trygonometrii z jej początków

-Wreszcie, pozostałe liczby to nieoznakowane są kuzynami.

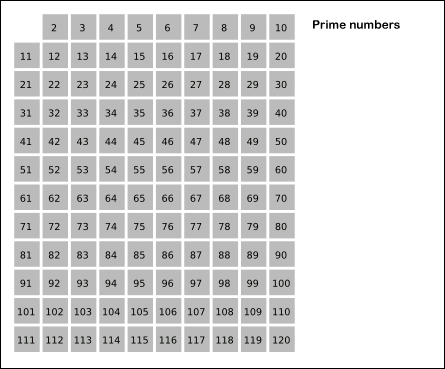Rysunek 2. ERATOSTENES Animacja przesiewowa. Źródło: Wikimedia Commons.

Ćwiczenia

- Ćwiczenie 1

Korzystając z wielomianu Eulera dla liczb pierwszych, znajdź 3 liczby większe niż 100.

Rozwiązanie

Jest to wielomian, który Euler zaproponował znalezienie liczb pierwszych, które działają dla n wartości od 0 do 39.

P (n) = n² + N + 41

Za pośrednictwem tanteo wybieramy wartość n, na przykład n = 8:

P (8) = 8² + 8 + 41 = 113

Ponieważ n = 8 wytwarza liczbę pierwszą większą niż 100, wówczas oceniamy wielomian dla n = 9 i n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Ćwiczenie 2

Dowiedz się, czy następujące liczby to kuzyni:

a) 13

b) 191

Rozwiązanie

13 jest wystarczająco mały, aby użyć małego twierdzenia Fermata i pomocy kalkulatora.

Używamy a = 2, aby liczby nie były zbyt duże, chociaż można je również użyć a = 3, 4 lub 5:

2¹³ - 2 = 8190

8190 jest podzielne między 2, ponieważ jest to nawet, dlatego 13 jest kuzynem. Czytelnik może go potwierdzić, wykonując ten sam test z A = 3.

Rozwiązanie b

191 jest bardzo duży, aby wypróbować twierdzenie i wspólny kalkulator, ale możemy pokonać podział między każdą liczbą pierwszą. Pomijamy podzielić przez 2, ponieważ 191 nie jest równe, a podział nie będzie dokładny lub stosunek mniejszy niż 2.

Próbowaliśmy podzielić przez 3:

191/3 = 63 666…

I nie daje dokładnego, ani iloraz jest mniejszy niż dzielnik (63 666 ... jest większy niż 3)

Nadal testujemy 191 przez kuzynów 5, 7, 11, 13, a dokładny podział nie jest osiągnięty, ani stosunek mniejszy niż dzielnik. Dopóki nie podzieli się między 17:

191/17 = 11, 2352 ..

Ponieważ nie jest dokładne i 11 3352 ... jest mniej niż 17, liczba 191 jest kuzynem.

Bibliografia

1. Baldor, a. 1986. Arytmetyka. Codex Editions and Dystrybucje.
2. Prieto, c. Liczby Primo. Źródło: strony.Matem.Unam.MX.
3. Właściwości liczb pierwszych. Odzyskany z: Mae.UFL.Edu.
4. Smartick. Liczby Primo: Jak je znaleźć z sito eratostenes. Odzyskany z: Smartick.Jest.
5. Wikipedia. Liczba pierwsza. Odzyskane z: jest.Wikipedia.org.