Reynolds numer Po co to jest, jak jest obliczane, ćwiczenia

On Numer Reynoldsa (R_I) Jest to wymiarowa ilość liczbowa, która ustanawia związek między siłami bezwładności a siły lepkości płynu ruchu. Siły bezwładnościowe są określane przez drugie prawo Newtona i są odpowiedzialne za maksymalne przyspieszenie płynu. Siły lepkie są siłami przeciwstawnymi ruchem płynu.

Liczba Reynoldsa jest stosowana do dowolnego rodzaju przepływu płynu, takiego jak przepływ w przewodach okrągłych lub niecirdzeniowych, w kanałach otwartych, a przepływ wokół zanurzonych ciał.

Wartość liczby Reynoldsa zależy od gęstości, lepkości, prędkości płynu i wymiarów bieżącej trasy. Zachowanie płynu w zależności od ilości rozpraszanej energii z powodu tarcia będzie to zależeć od tego, czy przepływ jest laminarny, turbulentny czy pośredni. Z tego powodu konieczne jest znalezienie sposobu na określenie rodzaju przepływu.

Jednym ze sposobów określenia tego jest metody eksperymentalne, ale wymaga dużej precyzji w pomiarach. Innym sposobem określenia rodzaju przepływu jest uzyskanie liczby Reynoldsa.

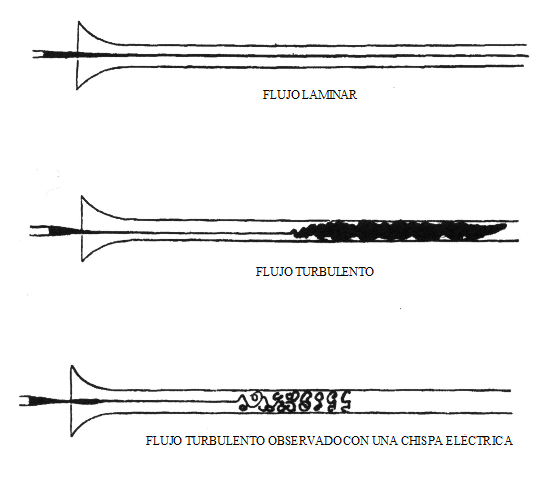
Przepływ wody obserwowany przez Osborne Reynolds [przez Osborne Reynolds (https: // commons.Wikimedia.org/wiki/file: Reynolds_Observations_Urbulence_1883.Svg)]

W 1883 r.

[TOC]

Do czego służy numer Reynoldsa?

Liczba Reynoldsa służy do określenia zachowania płynu, to znaczy w celu ustalenia, czy przepływ płynu jest laminarny czy turbulentny. Przepływ jest laminarny, gdy siły lepkie, które przeciwstawą się ruchowi płynu, są tymi, które dominują, a płyn porusza się z wystarczająco małą prędkością i w trajektorii prostoliniowej.

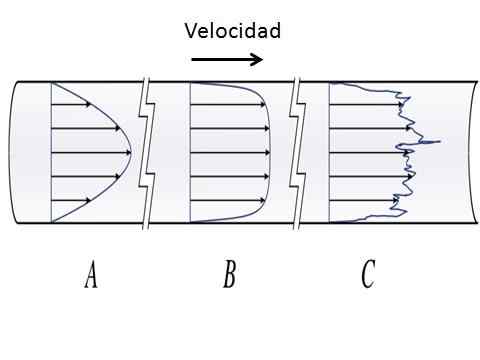Prędkość płynu, która porusza się przez okrągły kanał do przepływu laminarnego (A) i przepływu turbulentnego (B i C). [Autor: Olivier Cleynen (https: // commons.Wikimedia.org/wiki/file: PIPE_FLOW_VELOCITY_DISTRIBUSION_LAMINAR_UBULULTY.Svg)]

Płyn z przepływem laminarnym zachowuje się tak, jakby były nieskończonymi warstwami, które przesuwają się po pozostałych, w uporządkowanym sposób, bez mieszania. W przewodach okrągłych przepływ laminarny ma profil prędkości parabolicznej, z maksymalnymi wartościami w środku kanału i minimalnymi wartościami w warstwach w pobliżu powierzchni kanału. Wartość liczby Reynoldsa w przepływie laminarnym wynosi R_I<2000.

Przepływ jest turbulentny, gdy siły bezwładności są dominujące, a płyn porusza się z zmiennymi zmianami nieregularnej prędkości i trajektorii. Turbulentne przepływ jest bardzo niestabilne i ma transfery ruchu między cząstkami płynu.

Może ci służyć: fluor wapnia (CAF2): struktura, właściwości, zastosowania

Gdy płyn krąży w okrągłym kanale, z turbulentnym przepływem, warstwy płynu przecinają się ze sobą, tworząc wir, a ich ruch jest chaotyczny. Wartość liczby Reynoldsa dla turbulentnego przepływu w kierunku okrągłym wynosi R_I > 4000.

Przejście między przepływem laminarnym a przepływem turbulentnym występuje dla wartości liczby Reynoldsa między 2000 I 4000.

Jak to jest obliczane?

Równanie zastosowane do obliczenia liczby Reynoldsa w okrągłym kanodzie przekroju jest:

R_I = ρvd/η

ρ = Gęstość płynu (kg/m³)

V = Natężenie przepływu (M³/S)

D = Liniowy wymiar charakterystyczny płyn podróżny, który w przypadku przewodu kołowego reprezentuje średnicę.

η = Dynamiczna lepkość płynu (Rocznie.S)

Związek między lepkością a gęstością jest zdefiniowany jako lepkość kinematyczna v = η/ρ, A twoja jednostka jest M²/S.

Równanie liczby Reynoldsa w zależności od lepkości kinematycznej wynosi:

R_I = Vd/v

W kanałach i kanałach z nieczystymi przekrojami charakterystyczny wymiar jest znany jako średnica hydrauliczna D_H i reprezentuje uogólniony wymiar ścieżki płynu.

Uogólnione równanie do obliczenia liczby Reynoldsa w kanałach z nieczystymi przekrojami wynosi:

R_I = ρv 'd_H /η

V '= Średnia szybkość przepływu =WCHODZI

Średnica hydrauliczna D_H ustanawia związek między tym obszarem DO przekroju prądu przepływowego i mokrego obwodu P_M .

D_H = 4a/p_M

Mokry obwód P_M Jest to suma długości ścian kanału lub kanału, które są w kontakcie z płynem.

Możesz także obliczyć liczbę płynu Reynoldsa otaczającego obiekt. Na przykład kula zanurzona w płynie, poruszając się z prędkością V. Kula doświadcza siły oporu F_R zdefiniowane przez równanie Stokesa.

F_R = 6πrvη

R = Sphere Radio

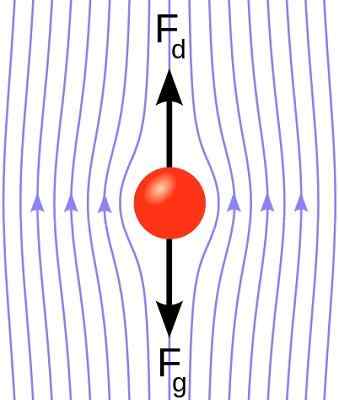Profil prędkości kuli zanurzony w płynie. Drag Force sprzeciwia się sile grawitacji. [Autor: KraaaNennest (https: // commons.Wikimedia.org/wiki/plik: Stokes_Sphere.Svg)]

Reynolds liczba kuli z prędkością V Zanurzony w płynie to:

R_I = ρv r /η

R_I<1 cuando el flujo es laminar y R_I > 1 Gdy przepływ jest burzliwy.

Rozwiązane ćwiczenia

Poniżej znajdują się trzy ćwiczenia aplikacyjne liczby Reynoldsa: przewód kołowy, kanał prostokątny i kula zanurzona w płynie.

Może ci służyć: Cięcie: jak obliczany i rozwiązany jest

Liczba Reynoldsa w okrągłym kanale

Obliczyć liczbę glikolu propylenowego Reynoldsa 20 °C w przewodzie o średnicy okrągłej 0,5 cm. Wielkość natężenia przepływu jest 0,15 m³/S. Jaki jest rodzaj przepływu?

D =0,5 cm = 5.10^-3M (Charakterystyczny wymiar)

Gęstość płynu jest ρ = 1036 g/cm³= 1036 kg/ m³

Lepkość płynu jest η = 0,042 PA · S = 0,042 kg/m.S

Szybkość przepływu jest V = 0,15 m³/S

Równanie liczb Reynoldsa jest stosowane w okrągłym przewodzie.

R_I =ρTY/η

R_I = (1036 kg/ m³X0,15 m³/s x 5.10^-3M)/(0,042 kg/m.s) = 18,5

Przepływ jest laminarny, ponieważ wartość liczby Reynoldsa jest niska w odniesieniu do relacji R_I<2000

Liczba Reynoldsa w prostokątnym kanale

Określić rodzaj przepływu etanolu, który przepływa z prędkością 25 ml/min w prostokątnej rurce. Wymiary sekcji prostokątnej wynoszą 0,5 cm i 0,8 cm.

Gęstość ρ = 789 kg/m³

Dynamiczna lepkość η = 1 074 MPa · s = 1074.10^-3 kg/m.S

Najpierw ustalono średnie natężenie przepływu.

V ' =WCHODZI

V = 25 ml/min = 4,16.10^-7M³/S

Przekrój jest prostokątny, którego boki wynoszą 0,005 m i 0,008 m. Obszar krzyżowy to A = 0,005 m x 0,008m = 4.10^-5M²

V ' = (4.16.10^-7M³/S) /(4.10^-5M²) = 1,04 × 10^-2SM

Mokry obwód jest sumą boków prostokąta.

P_M=0,013 m

Średnica hydrauliczna wynosi D_H = 4a/p_M

D_H = 4 × 4.10^-5M²/0,013 m

D_H= 1,23.10^-2M

Liczba Reynoldsa jest uzyskiwana z równania R_I = ρv 'd_H /η

R_I = (789 kg/m³X1,04 × 10^-2m/s x1.23.10^-2m)/ 1074.10^-3 kg/m.S

R_I = 93974

Przepływ jest burzliwy, ponieważ liczba Reynoldsa jest bardzo duża (R_I> 2000)

Reynolds liczba kuli zanurzonych w płynie

Cząsteczka sferyczna z lateksu z polystirenu, którego promień jest R= 2000 nm Jest wrzucony pionowo w wodzie z początkową prędkością wielkości V₀= 10 m/s. Określ liczbę Reynoldsa cząstki zanurzonej w wodzie

Gęstość cząsteczek  ρ = 1,04 g/cm³ = 1040 kg/m³

R= 2000 nm = 0,000002 m

Gęstość wody ρ_Ag= 1000 kg/m³ 

Breja η =0,001 kg/(m · s)

Liczba Reynoldsa jest uzyskiwana przez równanie R_I = ρv r /η

R_I = (1000 kg/m³X10 m/s X 0,000002 m)/ 0,001 kg/(m · s)

R_I = 20

Numer Reynoldsa wynosi 20. Przepływ jest turbulentny.

Aplikacje

Liczba Reynoldsa odgrywa ważną rolę w mechanice płynów i transferu termicznym, ponieważ jest to jeden z głównych parametrów charakteryzujących się płynem. Niektóre z twoich aplikacji są wymienione poniżej.

Może ci służyć: fale stacjonarne: wzory, cechy, typy, przykłady

1-IT służy do symulacji ruchu organizmów, które poruszają się po ciekłej powierzchnia.

2-IT ma praktyczne zastosowania w przepływie rur i w kanałach krążenia cieczy, zamknięte przepływy, szczególnie w porowatych mediach.

3 w zawiesinach cząstek stałych zanurzonych w płynie i emulsjach.

4-Numer Reynoldsa jest stosowany do testów tunelu aerodynami.

5-IT służy do modelowania ruchu owadów w powietrzu.

6-Projekt reaktora chemicznego wymaga użycia liczby Reynoldsa do wyboru modelu przepływu zgodnie ze stratami obciążenia, zużycia energii i powierzchni przenoszenia ciepła.

7-In W prognozy przenoszenia ciepła składników elektronicznych (1).

8 w nawadnianym procesie ogrodów i sadów, w których potrzebny jest przepływ wody, który wychodził z rur. Aby uzyskać te informacje, ustalono utratę obciążenia hydraulicznego związanego z tarciem między wodą a ścianami rur. Utrata obciążenia jest obliczana po uzyskaniu liczby Reynoldsa.

Tunel aerodynamiczny [autor: Juan Kulichevsky (https: // commons.Wikimedia.Org/Wiki/File: T%C3%BANEL_DE_VIENTO_ (35351654140).Jpg)]

Zastosowania biologii 

W biologii badanie ruchu organizmów żywych przez wodę lub w płynach o właściwościach podobnych do wody wymaga uzyskania liczby Reynoldsa, która będzie zależeć od wielkości organizmów i prędkości, z jaką poruszają się.

Bakterie i organizmy jednokomórkowe mają bardzo niską liczbę Reynoldsa (R_I<<1), w konsekwencji, przepływ ma profil prędkości laminarnej z przewagą sił lepkich.

Organizmy zbliżone do mrówek (do 1 cm) mają liczbę Reynoldsa rzędu 1, co odpowiada systemowi przejściowe, w którym siły bezwładności działające na ciele są równie ważne jak siły lepkie płynu.

W większych organizmach, takich jak ludzie liczba Reynoldsa jest bardzo duża (R_I>> 1).

Bibliografia

1. Zastosowanie modeli przepływu liczbowych o niskiej reynoldach do przewidywania elektronicznego transferu ciepła komponentu. Rodgers, P i Eveloy, V. NV: s.N., 2004, IEEE, vol. 1, str. 495-503.
2. Mott, R L. MECHANIKA PŁYWNYCH. Berkeley, Kalifornia: Pearson Prentice Hall, 2006, t. Siema.
3. Collieu, A M i Powney, D J. Właściwości mechaniczne i tematyczne materiałów. New York: Crane Russak, 1973.
4. Kay, J M i Nedderman, r m. Wprowadzenie do mechaniki płynów i transferu ciepła. New York: Cambridge University Press, 1974.
5. Happel, J i Brenner, H. Mechanika płynów i procesu transportu. Hingham, MA: Martinuss Nijhoff Publishers, 1983.