Numer koordynacyjny Czym jest, obliczenia, przykłady

On Numer koordynacyjny Jest to ilość atomów, jonów lub cząsteczek, które oddziałują z centrum związków jonowych i koordynacyjnych. Ta koncepcja można również zastosować do cząsteczek, biorąc pod uwagę, ile atomów jest ze sobą powiązanych zamiast liczby ich linków.

Liczba ta jest ważna, ponieważ określa geometrie kompleksów, gęstość ich faz materialnych, a nawet stereochemiczny (przestrzenny) charakter ich reaktywności. Aby uprościć ich definicję, są one uważane za sąsiad w ogóle otaczającej określone centrum.

W obszarze monet możemy docenić to, co oznacza liczba koordynacji

Rozważmy na przykład podłoga złożona z górnych monet obrazów. Wszystkie monety są tego samego rozmiaru, a jeśli każdy jest obserwowany, jest otoczony przez sześć innych; Oznacza to, że mają sześciu sąsiadów, a zatem numer koordynacyjny (c.N.) Dla monet jest to 6. Ten sam pomysł rozciąga się teraz na trzy -wymiar przestrzeni.

Jeśli ich radia są nierówne, nie wszystkie będą miały ten sam numer koordynacyjny. Na przykład: im większa waluta, im więcej sąsiadów, będzie w stanie wchodzić w interakcje z większą liczbą monet. Odwrotnie dzieje się z małymi monetami.

[TOC]

Koncepcja numeru koordynacji

VS Radia jonowe. Numer koordynacyjny

Liczba koordynacji jest liczba najbliższych sąsiadów i którzy zasadniczo oddziałują bezpośrednio z centrum, które jest głównie jonem metali. Zamiast tego odłożyliśmy monety, aby rozważyć sfery.

Ten metalowy jon m^N+, Gdzie N Jest równy jego utlenianiu lub liczbie walencji, oddziałuje z innymi sąsiadami (jonowymi lub molekularnymi) zwanymi ligandami. Im wyższy N (+2, +3 itp.), mniejsze będzie m^N+ I w konsekwencji ligandowie będą zmuszone do dalszego podejścia do interakcji z M^N+.

Może ci służyć: tłuszcz butyczny: pozyskiwanie, typy, skład, zastosowania, korzyści

Poniższy obraz ilustruje powyższe:

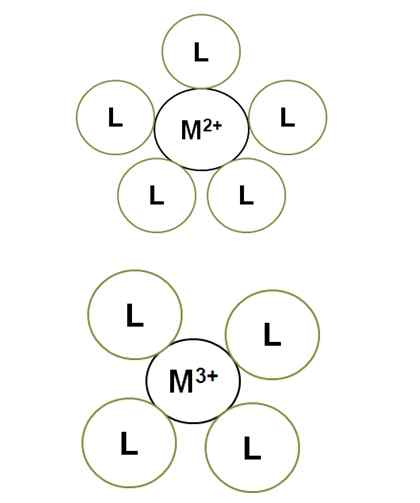Zmienność liczby koordynacji z centralnym obciążeniem jonów. Źródło: Gabriel Bolívar.

M²⁺ W oświeconym kompleksie ma liczbę koordynacji 5: jest otoczony 5 ligandami l. Tymczasem m³⁺ ma 4 numer koordynacyjny. To dlatego, że m³⁺, Aby mieć większą wielkość obciążenia, jego promień kurczy się, a zatem segregatory muszą zbliżyć się do więcej, co zwiększa ich elektroniczne odpychanie.

Dlatego nieporęczne jony centralne, takie jak te należące do metali blokowych F, lub do drugiego lub trzeciego okresu bloku D, Mają zwykle wyższe liczby koordynacji (c.N. > 6).

Gęstości

Załóżmy, że teraz kompleks M³⁺ ulega presji. Pojawi się punkt, w którym ciśnienie będzie takie, aby inny link był prawdopodobny skoordynowany lub wchodzi w interakcję z M³⁺. Oznacza to, że jego liczba koordynacji wzrośnie z 4 do 5.

Zasadniczo presja zwiększają liczbę koordynacji, ponieważ sąsiedzi zmuszają się do jonu centralnego lub atomu. W związku z tym fazy materialne tych substancji stają się gęstsze, bardziej zwarte.

Geometrie

Wyższe ilustracje nic nie mówią o geometriach wokół M²⁺ lub m³⁺. Wiemy jednak, że kwadrat ma cztery wierzchołki lub rogi, podobnie jak czworościan.

To rozumowanie stwierdzono, że geometria wokół M³⁺, którego c.N. To 4, musi być czworościenne lub kwadratowe. Ale który z dwóch? Tymczasem geometrie dla m²⁺, którego c.N. To jest 5, mogą być kwadratową piramidą lub trygonalną dwupiramidalną.

Każdy c.N. Powiązał kilka możliwych geometrii, które pozycjonują segregatory w sprzyjającej odległości, tak że istnieje między nimi najmniejsze odpychanie.

Może ci służyć: linki międzyatomiczne

Jak obliczono lub określony numer koordynacyjny?

Liczbę koordynacji można czasem obliczyć bezpośrednio na podstawie wspomnianego wzoru złożonego. Załóżmy, że kompleks anionowy [Ni (CN)₅]^3-. Jaki jest numer koordynacyjny dla jonów niklu lub²⁺? Wystarczy zaobserwować współczynnik stechiometryczny 5, który wskazuje, że istnieje 5 anionów cn^- skoordynowane lub wchodzące w interakcje z centrum Ni²⁺.

Jednak nie zawsze jest to łatwe. Na przykład związek CUCN wydaje się mieć liczbę koordynacji 1 zarówno dla Cu²⁺ Co do CN^-. Składa się jednak z faktycznie łańcuchów polimerowych Cu-CN-CU-CN, więc prawidłowy numer koordynacyjny wynosi 2.

Właśnie dlatego numer koordynacyjny jest lepszy do określenia go zamiast go obliczania. Jak? Określanie struktur jonowych lub molekularnych związków. Jest to możliwe dzięki technikom instrumentalnym, takim jak dyfrakcja X -Ray, neutrony lub elektrony.

Przykłady liczb koordynacji

Następnie i na koniec niektóre przykłady związków zostaną wymienione dla każdej z najczęstszych liczb koordynacyjnych. Podobnie, zostanie powiedziane, jakie są ich odpowiednie geometrie.

C.N. 2

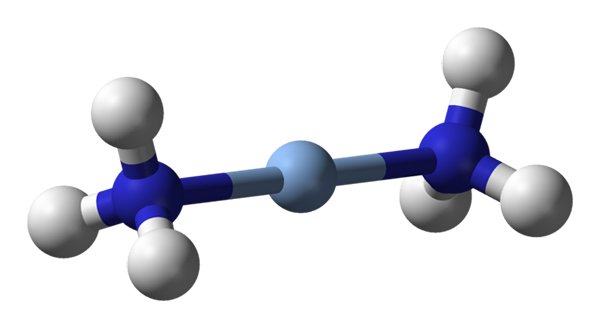Tutaj obserwuje się geometrię liniową [Ag (NH3) 2]+. Źródło: Benjah-BMM27 / Public Domena

A c.N. równe 2 oznacza, że ​​atom centralny lub jon ma tylko dwóch sąsiadów. Dlatego mówimy o związkach zobowiązujących o geometriach liniowych. Między nimi mamy:

-HG (rozdz₃)₂

-[AG (NH₃)₂]⁺

-Ph₃Paucl

C.N. 3

Każdy atom węgla w tym arkuszu grafitu jest podłączony do trzech innych, więc ma trzech sąsiadów. Źródło: Benjah-BMM27 / Public Domena

A c.N. równe 3 oznacza, że ​​atom centralny lub jon jest otoczony przez trzech sąsiadów. Następnie mamy geometrie, takie jak: płaszczyzna trygonalna (trójkątna), trygonalna piramida i forma T. Przykłady związków z tym numerem koordynacji to:

Może ci służyć: masa atomowa: definicja, typy, jak ją obliczyć, przykłady

-[Cu (CN)₃]^2-

-[PT (PCY₃)₃], Gdzie PCY odnosi się do ligandu tricyloheksyloofospiny

-Grafit

C.N. 4

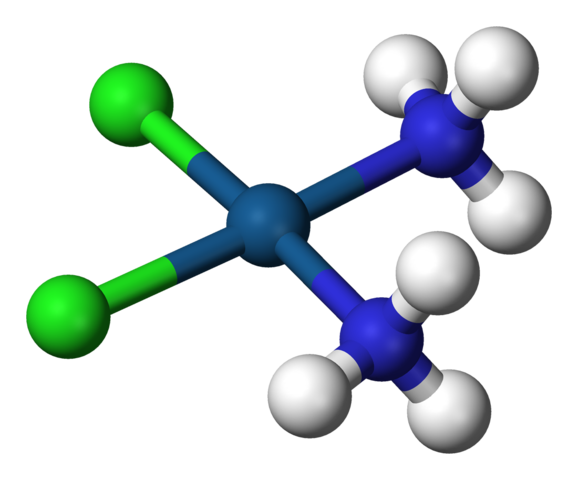Geometria kwadratowa cisplatyny, cis-PTCL2 (NH3) 2. Źródło: Benjah-BMM27 / Public Domena

A c.N. równe 4 oznacza, że ​​atom centralny lub jon jest otoczony przez czterech sąsiadów. Jego możliwe geometrie są czworościenne lub kwadratowe. Przykłady związków z tym numerem koordynacji mają następujące czynności:

-Ch₄

-Cocl₂Pyr₂

-CIS-PTCL₂(NH₃)₂

-[ALCL₄]^-

-[Muczeć₄]^2-

-Sncl₄

-[Cro₄]^2-

-[MNO₄]^2-

Wszystkie te przykłady, z wyjątkiem CIS-PTCL₂(NH₃)₂, Są geometrią czworościenną.

C.N. 5

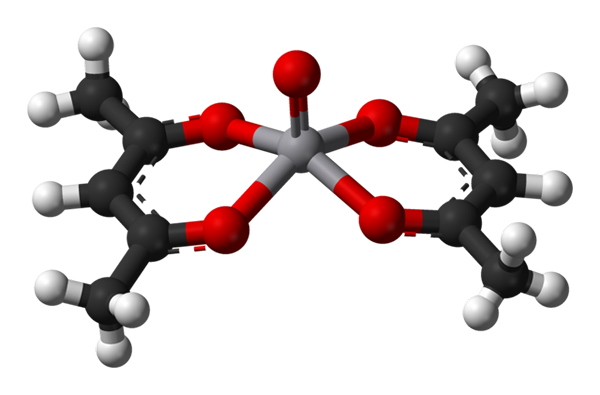Kwadratowa geometria piramidy dla VO (ACAC) 2. Źródło: Benjah-BMM27 / Public Domena.

A c.N. równe 5 oznacza, że ​​atom lub jon centralny jest koordynowany lub oddziaływany z pięcioma sąsiadami. Jego geometrie, już wspomniane, to kwadratowa piramida lub trygonalna dwupiramidalna. Jako przykłady mamy następujące:

-[COBRN (CH₂Ch₂Nme₂)₃]

-[Fe (CO)₅]

-VO (ACAC)₂, ACAC jest ligandem acetyloacetonatem

C.N. 6

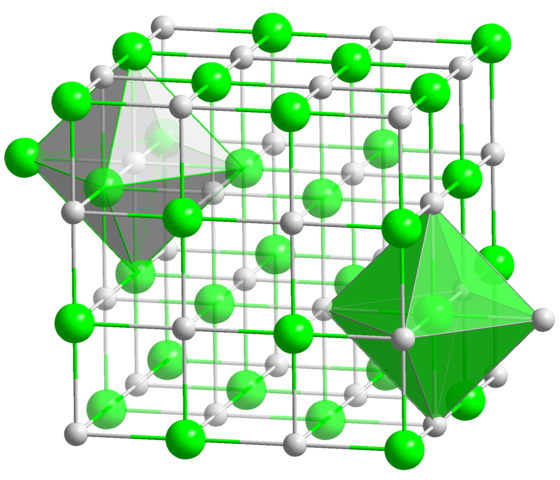W krystalicznej strukturze NaCl każdy jon Na+ i Cl- mają sześciu sąsiadów, więc jest to liczba koordynacji obu jonów (patrz oktahedra). Źródło: domena stała / publiczna

Jest to zdecydowanie najczęstsza liczba koordynacji wśród wszystkich związków. Pamiętaj o przykładach monety zasad. Ale zamiast jego ulubionej geometrii jest płaski sześciokąt, odpowiada genetronowi (normalnemu lub zniekształconej), oprócz trygonalnego pryzmatu. Niektóre z wielu przykładów związków z tym numerem koordynacji to:

-[Alf₆]^3-

-[Co (NH₃)₆]³⁺

-[ZR (wybierz₃)₆]^2-

-NaCl (tak, sól stołowa)

-Mos₂, Zwróć uwagę, że c.N. Dla tego związku nie jest 2

Inni

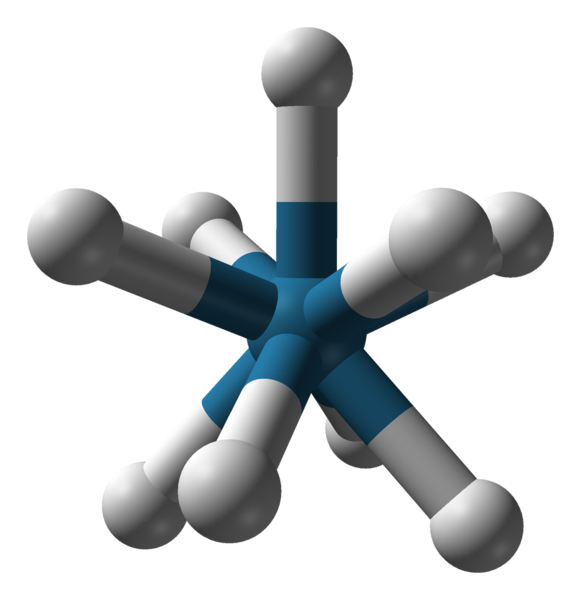Tripaded Triapadic Prisma Geometria anionu [reh9] 2-. Źródło: Benjah-BMM27 / Public Domena.

Istnieją inne liczby koordynacji, od 7 do 15. Tak c.N. Bądź wysoki, jon centralny lub atom musi być bardzo duży, mieć niewielki ładunek, a jednocześnie ligandowie muszą być bardzo małe. Niektóre przykłady związków z takimi C.N. Są poniżej i kończą:

-K₃[NBOF₆], C.N. 7 i geometria oktaedro

-[MO (CN)₈]^3-

-[ZR (Ox)₄]^2-, będąc wołem szczawianowym ligandem

-[Ret₉]^2-

-[Zmarszczyć brwi₃)₆]^2-, C.N. równe 12

Bibliografia

1. Whitten, Davis, Peck i Stanley. (2008). Chemia. (8 wyd.). Cengage Learning.
2. Shiver & Atkins. (2008). Chemia nieorganiczna. (Czwarta edycja). MC Graw Hill.
3. Wikipedia. (2020). Numer koordynacyjny. Źródło: w:.Wikipedia.org
4. Redaktorzy Enyclopaedia Britannica. (S.F.). Numer koordynacyjny. Odzyskane z: Britannica.com
5. Prof. Robert J. Lancashire. (15 sierpnia 2020). Liczby koordynacji i geometria. Chemia librettexts. Odzyskane z: chem.Librettexts.org
6. Helmestine, Anne Marie, pH.D. (28 sierpnia 2020). Definicja numeru koordynacji w chemii. Odzyskane z: Thoughtco.com