Przykłady wewnętrznych i zewnętrznych kątów sprzężonych, ćwiczenia

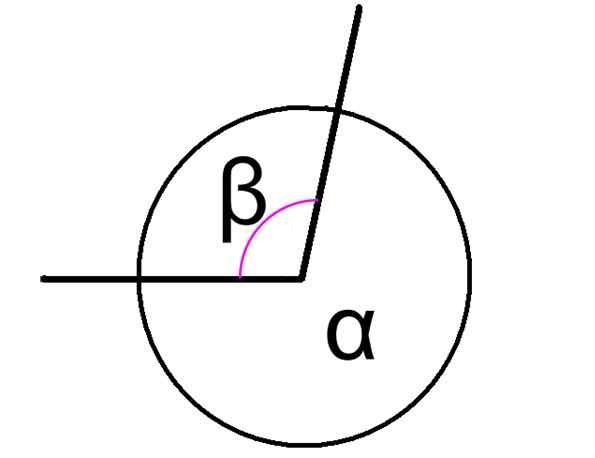
 skoniugowane kąty Są to te, które są dodawane w wyniku 360 °, niezależnie od tego, czy te kąty są sąsiadujące, czy nie. Rycina 1 pokazuje dwa skoniugowane kąty, oznaczone jako α i β.

W takim przypadku kąty α i β figury mają wspólny wierzchołek, a ich boki są powszechne, dlatego są sąsiadujące. Związek między nimi jest wyrażany w następujący sposób:

α + β = 360º

Rysunek 1. Dwa sprzężone kąty centralne, suma. Źródło: Wikimedia Commons. Nie dostarczył autora, który można odczytać w maszynie. THIAGO R RAMOS (na podstawie roszczeń dotyczących praw autorskich). [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/)] Jest to klasyfikacja kąta według jego suma. Inne ważne definicje obejmują Kąty komplementarne, którego suma wynosi 90 ° Dodatkowe kąty, co wynosi 180 °.

Z drugiej strony rozważmy teraz dwie równoległe linie wycięte przez siekant, których dyspozycja jest pokazana:

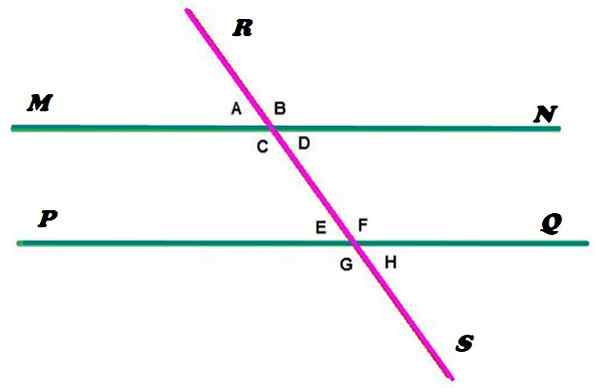Rysunek 2. Równoległe linie wycięte przez sekundę. Źródło: f. Zapata.

Linie MN i PQ są równoległe, podczas gdy linia RS wysycha, przecinając podobieństwa w dwóch punktach. Jak widać, ta konfiguracja określa tworzenie 8 kątów, do których została oznaczona małymi literami.

Cóż, zgodnie z definicją podaną na początku, kąty A, B, C i D są sprzężone. I w ten sam sposób są E, F, G i H, ponieważ oba przypadki są spełnione, że:

A+B+C+D = 360º

I

E+F+G+H = 360º

W tej konfiguracji dwa kąty są skoniugowane, jeśli są po tej samej stronie w odniesieniu do linii suszenia RS i oba są wewnętrzne lub zewnętrzne. W pierwszym przypadku mówi się o kątach Wewnętrzne koniugaty, Będąc w drugim, są one kątami Zewnętrzny koniugat.

[TOC]

Przykłady

Na ryc. 2, kąty zewnętrzne to te, które są poza regionem wyznaczone przez linie MN i PQ, są to kąty A, B, G i H. Podczas gdy kąty między dwiema liniami to C, D, E i F.

Może ci służyć: Koplanares Punkty: Równanie, przykład i rozwiązane ćwiczenia

Teraz konieczne jest przeanalizowanie, które kąty są po lewej, a po prawej.

Po lewej stronie RS znajdują się kąty A, C, E i G. A po prawej stronie znajdują się B, D, F i H.

Natychmiast przystępujemy do określenia par skoniugowanych kątów, zgodnie z definicją podaną w poprzedniej sekcji:

-A i g, zewnętrzne i po lewej stronie RS.

-D i F, wewnętrzne i po prawej stronie RS.

-B i H, zewnętrzne i po prawej stronie RS.

-C i E, wewnętrzne i po lewej stronie RS.

Właściwość skoniugowanych kątów między linkami równoległymi

Skoniugowane kąty między linii równoległych są uzupełniające, to znaczy ich suma jest równa 180 °. W ten sposób dla rysunku 2 zostały spełnione:

A + g = 180º

D + F = 180º

B + H = 180º

C + E = 180º

Odpowiadające pary kąty dla linii równoległej

Są to te, które są po tej samej stronie linii suszenia, nie są sąsiadujące, a jeden z nich jest wewnętrzny, a drugi jest zewnętrzny. Ważne jest, aby je wizualizować, ponieważ ich miara jest taka sama, ponieważ są przeciwne kątom przez wierzchołek.

Wracając do rysunku 2, odpowiednie kąty są identyfikowane jako:

-A i e

-C i g

-B i f

-D i h

Wewnętrzne kąty czworobocznego

Czworobokowe to 4 wielokąty, w tym kwadrat, prostokąt, trapez, równoległobok i romb, na przykład, na przykład. Niezależnie od jego formy, w którymkolwiek z nich jest spełnione, że suma jego wewnętrznych kątów wynosi 360º, dlatego są one zgodne z definicją podaną na początku.

Spójrzmy na niektóre przykłady czworoboku i sposobu obliczenia wartości jej wewnętrznych kąty zgodnie z informacjami z poprzednich sekcji:

Może ci służyć: jakie są 7 elementów obwodu?

Przykłady

a) Trzy kąty czworobocznego miary 75º, 110º i 70º. Ile powinien mierzyć pozostały kąt?

b) Znajdź wartość kąta ∠Q na rysunku 3 i.

c) Oblicz, ile mierzy kąt ∠A na rycinie 3 II.

Rozwiązanie

Niech α będzie brakującym kątem, spełnia się, że:

α + 75 º + 110º + 70º = 360 → α = 105º

Rozwiązanie b

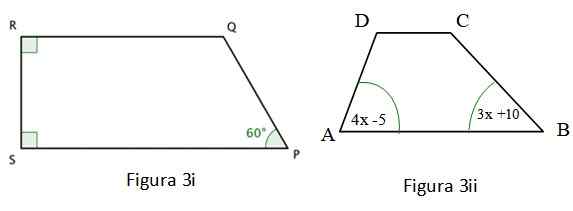
Rysunek 3I pokazano Trapezoid A dwa z jego wewnętrznych kąty są proste, które zostały wskazane za pomocą koloru kwadratu w zakątkach. W przypadku tego czworoboku weryfikowano następujące:

∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90º; ∠P = 60º

Dlatego:

∠ Q = 2 x 90º + 60º = 240º

Rozwiązanie c

Czworobok na ryc. 3 II jest również trapezem, dla którego spełnione są następujące:

∠A + ∠B + ∠C + ∠D = 360º

Dlatego:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

x = 25

Aby określić kąt wymagany w instrukcji, stosuje się, że ∠A = 4x - 5. Zastępując wartość x wcześniej obliczoną, następuje, że ∠A = (4 × 25) -5 = 95º

Ćwiczenia

- Ćwiczenie 1

Wiedząc, że jeden z pokazanych punktów jest wart 125, znalezienie miar pozostałych 7 kąta na poniższym rysunku i uzasadnienie odpowiedzi.

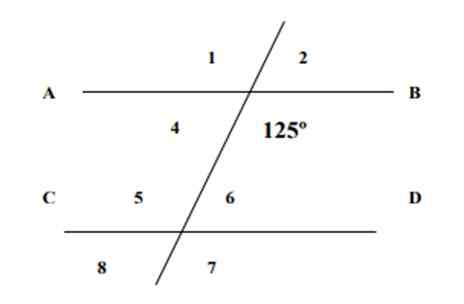Rysunek 4. Linie i kąty ćwiczenia 1. Źródło: f. Zapata.

Rozwiązanie

Kąt 6 i kąt 125 są wewnętrznym koniugatem, którego suma jest warta 180º, zgodnie z właściwością sprzężonych kąta, zatem:

∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º

Z drugiej strony ∠6 i ∠8 są przeciwnymi kątami przez wierzchołek, którego miara jest taka sama. Dlatego ∠8 mierzy 55º.

Może ci służyć: algebra wektorowa

Kąt ∠1 jest również przeciwny wierzchołkowi przy 125, wówczas możemy potwierdzić, że ∠1 = 125º. Możemy również odwołać się do faktu, że odpowiadające pary kąty mają tę samą miarę. Na rysunku te kąty to:

∠7 = 125 °

∠2 = ∠6 = 55 °

∠1 = ∠5 = 125º

∠4 = ∠8 = 55 °

- Ćwiczenie 2

Znajdź wartość x na poniższym rysunku i wartości wszystkich stron:

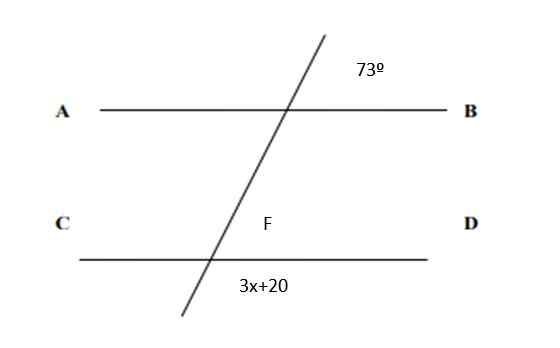Rysunek 5. Linie i kąty do ćwiczeń 2. Źródło: f. Zapata.

Rozwiązanie

Ponieważ są odpowiadające parom, wynika z tego, że f = 73º. Z drugiej strony suma par sprzężonych wynosi 180º, dlatego:

3x + 20º + 73º = 180º

3x = 180º - 73º -20º = 87

Wreszcie wartość x to:

x = 87/3 = 29

Jeśli chodzi o wszystkie kąty, pojawiają się one wymienione na poniższym rysunku:

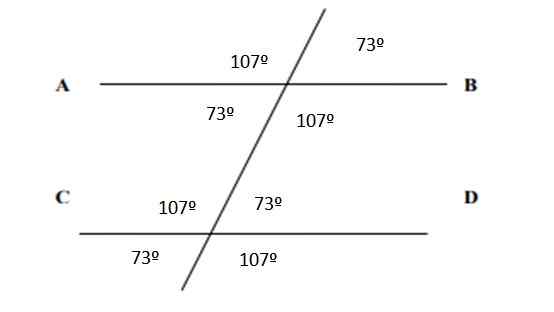Rysunek 6. Kąty powodujące ćwiczenie 2. Źródło: f. Zapata.

Bibliografia

1. Grupy kątowe. Wyjaśnienie uzupełniające, uzupełniające i wyjaśniające. Odzyskane z: thisiget.com/
2. Baldor, a. 1983. Płaska, przestrzeń i geometria trygonometrii. Grupa kulturowej ojczyzny.
3. Corral, m. Mathematics Librettexts: Angles. Odzyskane z: matematyki.Librettexts.org.
4. Mathmania. Klasyfikacja i konstruowanie kątów według ich pomiaru. Odzyskane z: Mathemania.com/
5. Wentworth, G. Geometria planety. Odzyskane z: Gutenberg.org.
6. Wikipedia. Skoniugowane kąty. Odzyskane z: jest.Wikipedia.org.