Coplanares Punkty równania, przykładowe i rozstrzygnięte ćwiczenia

 Punkty Coplanares Wszystkie należą do tej samej płaszczyzny. Dwa punkty to zawsze koplanares, ponieważ punkty te definiują linię, przez którą przechodzą płaskie nieskończone. Następnie oba punkty należą do każdego z planów przechodzących przez linię i dlatego zawsze będą koplanares.

Z drugiej strony trzy punkty definiują pojedynczy płaszczyznę, którego następuje, że trzy punkty zawsze będą koplanares.

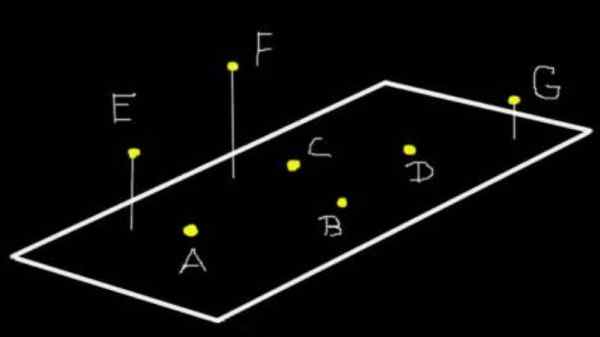
Rysunek 1. A, B, C i D są koplanaresami do płaszczyzny (ω). E, f i g nie są coplanares a (ω), ale jeśli są koplanaresem do płaszczyzny, trzy definiują trzy. Źródło: f. Zapata.

Ponad trzy punkty może to być koplanar, czy nie. Na przykład na rycinie 1 punkty A, B, C i D są koplanaresami do płaszczyzny (ω). Ale e, f i g nie są koplanaresami a (ω), chociaż są koplanaresami do płaszczyzny, że trzy definiują.

[TOC]

Równanie płaszczyzny, biorąc pod uwagę trzy punkty

Równanie płaszczyzny określonej przez trzy znane punkty a, b, c jest matematyczną relacją, która gwarantuje, że każdy punkt p ogólnych współrzędnych (x, y, z), który wypełnia równanie, należy do wspomnianego płaszczyzny. 

Poprzednie stwierdzenie jest równoważne stwierdzeniu, że jeśli p współrzędnych (x, y, z) spełnia równanie płaskie, to wspomniany punkt będzie copatar z trzema punktami a, b, c, który określił płaszczyznę.

Aby znaleźć równanie wspomnianego samolotu, zacznijmy od znalezienia wektorów Ab I AC:

Ab = [Bx - ax, przez - ay, bz - az]

AC = [CX - ax, Cy - AY, CZ - AZ]

Produkt wektorowy Ab X AC Powoduje wektor prostopadły lub normalny do płaszczyzny określonej przez punkty a, b, c.

Dowolny punkt współrzędnych (x, y, z) należy do płaszczyzny, jeśli prawdą jest, że wektor AP jest prostopadle do wektora Ab X AC, co jest gwarantowane, jeśli zostanie spełnione:

Może ci służyć: decagon: regularne, nieregularne, nieruchomości, przykłady

AP • (AB X AC) = 0

Jest to równoznaczne z stwierdzeniem, że potrójny produkt AP, Ab I AC Bądź NULL. Poprzednie równanie można napisać w sposób macierzy:

Przykład

Niech punkty a (0, 1, 2); B (1, 2, 3); C (7, 2, 1) i D (Do, 0, 1). Jaka wartość powinna mieć Do tak, że cztery punkty to koplanares?

Rozwiązanie

Aby znaleźć wartość A, konieczne jest, aby punkt D był częścią płaszczyzny określonej przez a, b i c, co jest gwarantowane, jeśli równanie płaskie spełnia.

Rozwijanie determinanta, które mamy:

A (-1-1) + 1 (-1 -7) -1 (1-7) = -2a -8 + 6 = -2a -2 = 0

Poprzednie równanie wskazuje, że A = -1 Aby spełnić równość. Innymi słowy, jedyny sposób, w jaki punkt D (Do, 0.1) być koplaną z punktami A, B i C Do Valga -1. W przeciwnym razie nie będzie to koplan.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Płaszczyzna przecina osie kartezjańskie x, y, z odpowiednio w 1, 2 i 3. Przecięcie wspomnianej płaszczyzny z osiami określa punkty A, B i C. Znajdź element DZ punktu D, którego elementy kartezjańskie to:

 D (-GZ, dz+1, dz) 

Pod warunkiem, że D jest koplan z punktami A, B i C. 

Rozwiązanie

Gdy znane są przechwytywanie płaszczyzny z osiami kartezjańskimi, można zastosować segmentową formę równania płaskiego:

x/1 + y/2 + z/3 = 1

Ponieważ punkt D musi należeć do poprzedniego samolotu, musisz:

-Dz/1 + (dz + 1)/2 + dz/3 = 1

To jest do powiedzenia:

-Dz + dz/2 + ½ + dz/3 = 1

Dz (-1 + ½ + ⅓) = ½ 

Dz (-1/6⅙) = ½ 

Dz = -3 

Z powyższego wynika z tego, że punkt D (3, -2, -3) ma sprzężenie z punktami A (1, 0, 0); B (0, 2, 0) i C (0, 0, 3).

Może ci służyć: trójkątne kryteria podobieństwa

- Ćwiczenie 2

Określić, czy punkty A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) i D (2, 3, 1) to koplanares.

Rozwiązanie

Tworzymy matrycę, której szeregi są współrzędne D-A, B-A i C-A. Wówczas obliczanie wyznacznika i jest weryfikowane, czy zero.

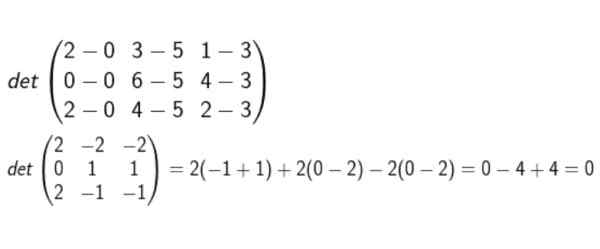
Po wykonaniu wszystkich obliczeń stwierdza się, że są to koplanares.

- Ćwiczenie 3

Dwie linie są podane w przestrzeni. Jednym z nich jest linia (r), której równanie parametryczne to:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

A druga to linia, której równanie to:

(S): x + 2 y = 1; Z = -1

Zademonstrować, że (r) i (s) są one proste, to znaczy są w tej samej płaszczyźnie.

Rozwiązanie

Zacznijmy dowolnie dwa punkty na linii (R) i dwa na linii:

Straight (R): λ = 0; A (1, 1, 1) i λ = 1; B (3, 0, 1)

Zróbmy x = 0 na linii (y)=> y = ½; C (0, ½, -1). A z drugiej strony, jeśli to zrobimy y = 0 => x = 1; D (1, 0, -1).

Oznacza to, że wzięliśmy punkty A i B, które należą do linii (R) i punktów C i D, które należą do linii (y). Jeśli te punkty to koplanares, dwie linie również będą.

Teraz decydujemy się wskazać, jak obrotić, a następnie znajdziemy współrzędne wektorów Ab, AC I OGŁOSZENIE. W ten sposób dostajesz:

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => AC= (-1, -1/2, -2)

D -A: (1-1, 0 -1, -1 -1) => OGŁOSZENIE= (0, -1, -2)

Następnym krokiem jest zbudowanie i obliczenie wyznacznika, którego pierwszym rządem jest współczynniki wektora Ab, Drugi rząd to AC i trzeci rząd wektor OGŁOSZENIE:

Może ci służyć: Miletus taki twierdzenie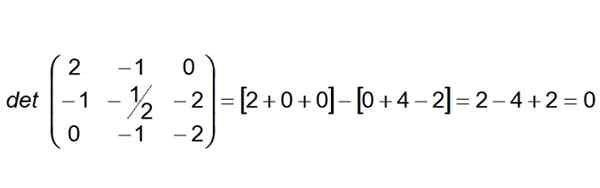

Jak okazuje się determinant zerowy, możemy stwierdzić, że cztery punkty to koplanarios. Dodatkowo można powiedzieć, że linie (r) i (s) są również koplanaresami.

- Ćwiczenie 4

Linie (r) i (s) są koplanaresami, jak pokazano w ćwiczeniu 3. Znajdź równanie płaszczyzny, która je zawiera.

Rozwiązanie

Punkty a, b, c całkowicie definiują tę płaszczyznę, ale chcemy narzucić, że każdy punkt x współrzędnych (x, y, z) należą do tego samego.

X - a: (x -1, y -1, z - 1) => Topór= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => AC= (-1, -1/2, -2)

Tak, że x należy do płaszczyzny zdefiniowanej przez a, b, c i w której obrony (r) i (s) są konieczne, konieczne jest, aby wyznacznik utworzony w jego pierwszym rzędzie był unieważniony przez składniki Topór, w drugiej przez tych Ab I w trzecie AC:

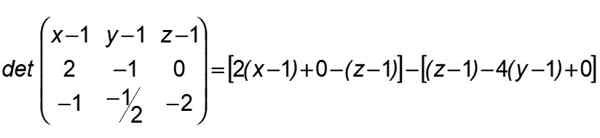
Po tym wyniku grupujemy w ten sposób:

2 (x-1) + 4 (y-1) -2 (z-1) = 0

I natychmiast widać, że można go tak przepisać:

x - 1 + 2y - 2 - z + 1 = 0

Dlatego x + 2y - z = 2 jest równaniem płaszczyzny zawierającej linie (r) i (s).

Bibliografia

1. Fleming, w. 1989. Prealculus Mathematics. Prentice Hall ptr.
2. Kolman, ur. 2006. Algebra liniowa. Edukacja Pearsona.
3. Lojalny, j. M. 2005. Płaska geometria analityczna. Mérida - Wenezuela: Wenezuelan redakcja C. DO.
4. Navarro, Rocio. Wektory. Odzyskane z: książki.Google.współ.Iść.
5. Pérez, c. D. 2006. Przedłużanie. Edukacja Pearsona.
6. Prenowitz, w. 2012. Podstawowe pojęcia geometrii. Rowman i Littlefield.
7. Sullivan, m. 1997. Przedłużanie. Edukacja Pearsona.