Środki pozycji, tendencja centralna i dyspersja

miary tendencji centralnej, dyspersji i pozycji, Są to wartości używane do prawidłowego interpretacji zestawu danych statystycznych. Można je opracować bezpośrednio, jak uzyskano z badania statystycznego lub można je zorganizować w grupach o równej częstotliwości, ułatwiając analizę.

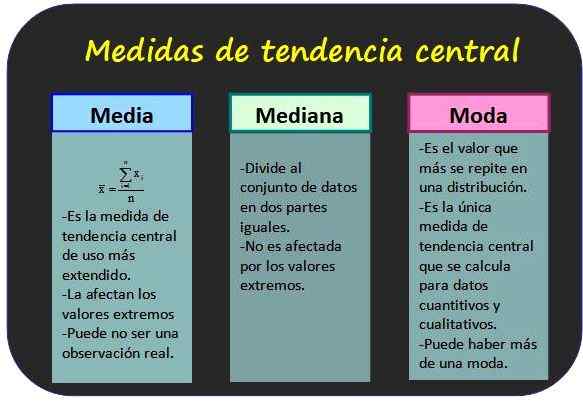
Trzy najbardziej znane środkowe miary trendów i niektóre z jego właściwości. Źródło: f. Zapata.

Miary tendencji centralnej

Pozwalają wiedzieć, jakie wartości dane statystyczne są zgrupowane razem.

Średnia arytmetyczna

Jest również znany jako średnia wartości zmiennej i jest uzyskiwana przez dodanie wszystkich wartości i podzielenie wyniku przez całkowitą liczbę danych.

• Średnia arytmetyczna dla danych bez grupowania

Być zmienną x, której nie ma danych bez organizowania lub grupowania, jej średnia arytmetyczna jest obliczana w następujący sposób:

I podsumowując notację:

Przykład

Właściciele górskiego hostelu turystycznego zamierzają wiedzieć, ile średnich odwiedzających pozostaje w obiektach. Aby to zrobić, przeprowadzono zapis dni trwałości 20 grup turystów, uzyskując następujące dane:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

Średnie dni, w których pozostają turyści, to:

= 2.5 dni

• Średnia arytmetyczna dla danych zgrupowanych

Jeśli dane zmienne są zorganizowane w bezwzględnej tabeli częstotliwości F_Siema A centra klasowe to x₁, X₂,…, X_N, Średnia jest obliczana przez:

W sumieniu lata:

Mediana

Mediana grupy n wartości zmiennej x jest centralną wartością grupy, pod warunkiem, że wartości są coraz bardziej uporządkowane. W ten sposób połowa wszystkich wartości jest niższa niż moda, a druga połowa jest większa.

• Medium danych niezgrupowych

Można przedstawić następujące przypadki:

-Liczba N Wartości zmiennej x  dziwne: Mediana to wartość, która jest w środku grupy wartości:

-Liczba N Wartości zmiennej x para: W tym przypadku mediana jest obliczana jako średnia z dwóch centralnych wartości grupy danych:

Przykład

Aby znaleźć medianę danych hostelu turystycznych, są pierwszymi, od co najmniej do największej:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Może ci służyć: jaka jest częstotliwość względna i jak jest obliczana?

Numer danych jest równy, dlatego istnieją dwa centralne dane: x₁₀ i x_jedenaście A ponieważ oba są warte 2, jej średnia.

Mediana = 2

• Medium zgrupowanych danych

Zastosowana jest następująca formuła:

Symbole w formule oznaczają:

-C: szerokość interwału zawierająca medianę

-B_M: dolna granica tego samego przedziału

-F_M: liczba obserwacji zawierających odstęp, do którego należy mediana.

-N: Całkowite dane.

-F_BM: liczba obserwacji przed przerwą zawierającą medianę.

Moda

Moda dla danych niezgrupowanych jest najczęstszą wartością częstotliwości, podczas gdy dla zgrupowanych danych jest to klasa najczęstszej. Jest uważany za modę za najbardziej reprezentatywne dane lub klasa dystrybucji.

Dwie ważne cechy tej miary to to, że zestaw danych może mieć więcej niż jedną modę, a moda można określić zarówno dla danych ilościowych, jak i danych jakościowych.

Przykład

Kontynuując dane hostelu turystycznego, ten, który jest najbardziej powtarzany, to 1, dlatego najbardziej zwykłą rzeczą jest to, że turyści pozostają 1 dzień w hostelu.

Miary dyspersji

Środki dyspersji opisują, w jaki sposób zgrupowane są dane dotyczące środków centralnych.

Zakres

Oblicza go odejmowanie głównych danych i drobnych danych. Jeśli ta różnica jest duża, jest to znak, że dane są rozproszone, podczas gdy małe wartości wskazują, że dane są zbliżone do średniej.

Przykład

Zakres danych hostelu turystycznych jest:

Zakres = 5-1 = 4

Zmienność

• Wariancja danych niezgrupowych

Aby znaleźć wariancję s² Konieczne jest najpierw znać średnią arytmetyczną, wówczas różnica jest obliczana na kwadrat między każdym danymi a średnią, wszystkie są dodawane i podzielone przez całkowitą obserwacje. Różnice te są znane jako Odchylenia.

Wariancja, która jest zawsze pozytywna (lub zerowa), wskazuje, jak daleko są obserwacje średniej: jeśli wariancja jest wysoka, wartości są bardziej rozproszone niż wtedy, gdy wariancja jest niewielka.

Przykład

Wariancją danych hostelu turystycznego jest:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Wariancja danych zgrupowanych

Aby znaleźć wariancję grupy zgrupowanych danych, są one wymagane: i) średnia, ii) częstotliwość f_Siema  które są całkowitymi danymi w każdej klasie i iii) x_Siema  lub wartość klasy:

Może ci służyć: rodzaje trójkątów

Odchylenie standardowe

Odchylenie standardowe jest dodatnim pierwiastkiem kwadratowym wariancji, więc ma przewagę nad wariancją: występuje w tych samych jednostkach, co zmienna w badanej, a zatem ma bardziej bezpośredni pomysł niż zamknięcie lub daleko, która jest zmienną średniej.

• Odchylenie standardowe dla danych nieogrupowych

Jest to określane po prostu poprzez znalezienie pierwiastka kwadratowego wariancji dla nieograniczonych danych:

 Przykład

Standardowe odchylenie danych hostelu turystycznego to:

S = √ (s²) = √1.95 = 1.40

• Odchylenie standardowe dla zgrupowanych danych

Jest to obliczane poprzez znalezienie pierwiastka kwadratowego wariancji dla zgrupowanych danych:

Miary pozycji

Mierniki pozycji Podziel uporządkowany zestaw danych na równe części. Mediana, oprócz tego, że jest miarą tendencji centralnej, jest również miarą pozycji, ponieważ dzieli całość na dwie równe części. Ale można uzyskać mniejsze części z kwartylami, decylami i percentylami.

Kwartyle

Kwartyle dzielą zestaw na cztery równe części, każda z 25 % danych. Są oznaczone jako Q₁, Q₂ i Q₃ A mediana to kwartyl q₂. W ten sposób 25% danych jest poniżej kwartylu Q₁, 50% poniżej kwartylu Q₂ lub mediana i 75% pod kwartylem Q₃.

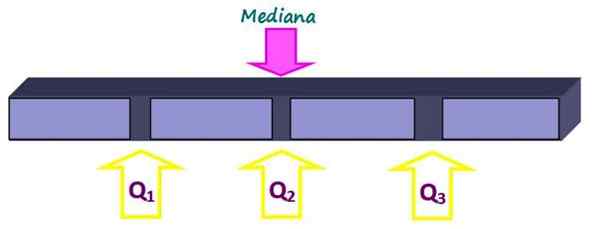Rysunek 2. Kwartyle dzielą zestaw danych na cztery równe części. Źródło: f. Zapata.

• Kwartyle dla danych niezgrupowych

Dane są uporządkowane, a suma jest podzielona na 4 grupy z tą samą liczbą danych. Pozycja pierwszego kwartylu znajduje się przez:

Q₁ = (n+1)/4

Będąc całkowitymi danymi. Jeśli wynikiem są całe dane odpowiadające tej pozycji, ale jeśli są dziesiętne, dane odpowiadające całej części z następującymi są uśredniane lub dla większej precyzji są liniowo interpolowane między wspomnianymi danymi.

Przykład

Pozycja pierwszego kwartylu Q₁ Dla danych hostelu turystycznego to:

Q₁ = (n+1) / 4 = (20+1) / 4 = 5.25

Jest to pozycja kwartylu 1, w wyniku czego jest dziesiętne, poszukiwane są dane X₅ i x_6, które są odpowiednio x₅ = 1 i x₆ = 1 i są one uśrednione, co wynika z:

Pierwszy kwartyl = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Pozycja drugiego kwartylu Q₂ Jest:

Może ci służyć: suma teleskopowa: jak jest rozwiązane i rozwiązane ćwiczenia

Q₂ = 2 (n+1)/4 = 10.5

Która jest średnią między x₁₀ i x_jedenaście i zbiega się z medianą:

Drugi kwartyl = mediana = 2

Trzecia pozycja kwartylowa jest obliczana przez:

Q₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Jest to również dziesięczne, dlatego x są uśredniane_piętnaście i x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Ale ponieważ oba są warte 4:

Trzeci kwartyl = 4

Ogólna formuła pozycji kwartyli w nieograniczonych danych jest:

Q_k = K (n+1)/4

Z k = 1,2,3.

• Kwartyle dla danych zgrupowanych

Są one obliczane podobnie do mediany:

Wyjaśnienie symboli to:

-B_Q: dolna granica przedziału zawierająca kwartyl

-C: Szerokość tego przedziału

-F_Q: Liczba obserwacji zawierała interwał kwartylu.

-N: Całkowite dane.

-F_BQ: Liczba danych przed przedziałem zawierającym kwartyl.

Decyle i percentyle

Decyle i percentyle dzielą zestaw danych odpowiednio na 10 równych części i 100 równych części, a ich obliczenia odbywa się analogiczne do obliczeń kwartyli.

• Decyle i percentyle dla danych niezgrupowych

Formuły są używane odpowiednio:

D_k = K (n+1)/10

Z k = 1,2,3… 9.

Decyl d₅ Musi być równe medianie.

P_k = K (n+1)/100

Z k = 1,2,3… 99.

Percentyl p_{pięćdziesiąt} Musi być równe medianie.

Przykład

W przykładzie hostelu turystycznego, pozycja D₃ Jest:

D₃ = 3 (20+1)/10 = 6.3

Jak ma uśrednioną liczbę dziesiętną x₆ i x_7, Oba równe 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Oznacza, że ​​3 dziesiąte danych jest poniżej x₇ = 1 i pozostałe powyżej.

• Decyle i percentyle dla zgrupowanych danych

Formuły są analogiczne do kwartyli. D służy do oznaczania decyleń i p dla percentyli, a symbole są interpretowane w podobny sposób:

Reguła empiryczna

Gdy dane są dystrybuowane symetrycznie, a rozkład jest nieimodalny, nazywana jest reguła  Zasada empiryczna albo Reguła 68 - 95 - 99, To grupuje je w następujących odstępach czasu:

• 68% danych jest w przedziale:

• 95% danych jest w przedziale:

• 99% danych jest w przedziale:

Przykład

W jakim przedziale wynosi 95% danych hostelu turystycznego?

Są w przedziale: [2.5-1.40; 2.5+1.40] = [1.1; 3.9].

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
3. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
4. Spiegel, m. 2009. Statystyka. Seria Schaum. 4 Ta. Wydanie. McGraw Hill.
5. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.