Formuły współczynnika określenia, obliczenia, interpretacja, przykłady

On Współczynnik determinacji Jest to liczba między 0 a 1, która reprezentuje ułamek punktów (x, y), który podąża za linią regulacji przez regresję zestawu danych z dwiema zmiennymi.

Jest również znany jako dobroć regulacji i jest oznaczony przez r². Aby to obliczyć, iloraz jest pobierany między wariancją danych ŷi oszacowanych przez model regresji a wariancją danych Yi odpowiadających każdemu XI danych.

R² = Sŷ / sy

Rysunek 1. Współczynnik korelacji dla czterech par danych. Źródło: f. Zapata.

Jeśli 100% danych znajduje się na linii funkcji regresji, współczynnik określenia wyniesie 1.

Przeciwnie, jeśli dla zestawu danych i określonej funkcji regulacji współczynnik R² Okazuje się, że jest równy 0.5, wtedy można powiedzieć, że regulacja jest zadowalająca lub dobra na 50%. 

Podobnie, gdy model regresji rzuca wartości r² mniej niż 0.5, wskazuje to, że wybrana funkcja regulacji nie dostosowuje się zadowalająco do danych, dlatego jest niezbędna do poszukiwania innej funkcji regulacji.

I kiedy Kowariancja albo Współczynnik korelacji Ma tendencję do zera, a następnie zmienne x i y z danych nie są powiązane, a zatem r² będzie miało również zero.

[TOC]

Jak obliczyć współczynnik określenia?

W poprzednim rozdziale powiedziano, że współczynnik ustalenia jest obliczany poprzez znalezienie ilorazu między wariancjami:

-Oszacowane przez funkcję regresji zmiennej i 

-Zmienna Yi odpowiadająca każdej zmiennej XI. 

W formie matematycznej pozostaje tak:

R² = Sŷ / sy

Z tej formuły wynika, że ​​r² reprezentuje odsetek wariancji wyjaśnionej przez model regresji. Alternatywnie można obliczyć R² Poprzez następujący wzór, całkowicie równoważny z poprzednim:

R² = 1 - (Sε / sy)

Gdzie Sε reprezentuje wariancję odpadów εi = ŷi - yi, podczas gdy SY jest wariancją zestawu danych danych. Aby określić ŷI, stosuje się funkcję regresji, co oznacza potwierdzenie, że ŷi = f (xi).

Może ci służyć: ułamek równoważny 3/5 (rozwiązanie i wyjaśnienie)

Wariancja zestawu danych Yi, z I od 1 do N jest obliczana w ten sposób:

Sy = [σ (yi -)² ) / (N-1)]

A następnie postępuj w podobny sposób dla Sŷ lub Sε.

Przypadek ilustracyjny

Poprzez pokazanie szczegółów sposobu, w jaki obliczanie Współczynnik determinacji Weźmy następujący zestaw czterech par danych: 

(X, y): (1, 1); (23); (3, 6) i (4, 7).

Dla tego zestawu danych proponuje się regulację regresji liniowej uzyskaną metodą minimum kwadratowego:

f (x) = 2.1 x - 1 

Stosując tę ​​funkcję regulacji, rówieśnicy są uzyskiwani:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) i (4, 7.4).

Następnie obliczamy średnią arytmetyczną dla x i y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Wariancja SY

SY = [(1–4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Wariancja sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Współczynnik determinacji r²

R² = Sŷ / sy = 7.35/7.58 = 0.97

Interpretacja

Współczynnik ustalenia dla ilustracyjnego przypadku rozważanego w poprzednim segmencie okazał się 0.98. To znaczy, że regulacja liniowa za pośrednictwem funkcji:

 f (x) = 2.1x - 1

98% wiarygodne jest wyjaśnienie danych, z którymi zostały uzyskane za pomocą minimalnej metody kwadratowej. 

Oprócz współczynnika ustalenia istnieje Współczynnik korelacji liniowej lub znany również jako współczynnik Pearsona. Ten współczynnik, oznaczony jako R, Jest to obliczane na podstawie następującej relacji:

R = sxy / (sx sy)

Tutaj licznik reprezentuje kowariancję między zmiennymi x i y, podczas gdy mianownik jest iloczynem odchylenia standardowego dla zmiennej x i odchyleniem standardowym dla zmiennej i.

Współczynnik Pearsona może przyjmować wartości między -1 do +1. Gdy ten współczynnik ma tendencję do +1, istnieje bezpośrednia korelacja liniowa między x i y. Jeśli zamiast tego ma tendencję do -1, istnieje korelacja liniowa, ale gdy X rośnie i maleje. Wreszcie, jest blisko 0, nie ma korelacji między dwiema zmiennymi.

Może Ci służyć: zgrupowane dane: przykłady i ćwiczenia rozwiązane

Należy zauważyć, że współczynnik określenia pokrywa się z kwadratem współczynnika Pearsona, tylko wtedy, gdy pierwszy został obliczony na podstawie regulacji liniowej, ale ta równość nie jest ważna dla innych nieliniowych korekt.

Przykłady

- Przykład 1

Grupa uczniów szkół średnich zamierza ustalić prawo empiryczne na okres wahadła w funkcji jego długości. Aby osiągnąć ten cel, wykonują serię pomiarów, w których mierzą czas oscylacji wahadła dla różnych długości, uzyskując następujące wartości:

Długość (m)	Okresy)
0.1	0,6
0,4	1.31
0,7	1,78
1	1.93
1.3	2.19
1.6	2.66
1.9	2.77
3	3.62

Poproszono o wykonanie wykresu dyspersji danych i dokonanie regulacji liniowej przez regresję. Ponadto pokaż równanie regresji i jego współczynnik określenia.

Rozwiązanie

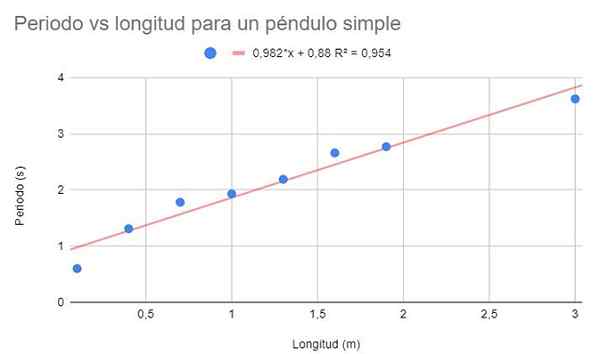Rysunek 2. Rozwiązanie graficzne ćwiczenia 1. Źródło: f. Zapata.

Można zaobserwować dość wysoki współczynnik determinacji (95%), aby można było uznać, że regulacja liniowa jest optymalna. Jeśli jednak punkty są obserwowane razem, wydaje się, że mają tendencję do zakrzywiania. Ten szczegół nie jest rozważany w modelu liniowym.

- Przykład 2

W przypadku tych samych danych z przykładu 1 zrób wykres dyspersji danych. Przy tej okazji, w przeciwieństwie do przykładu 1, należy dokonać dostosowania regresji za pomocą potencjalnej funkcji.

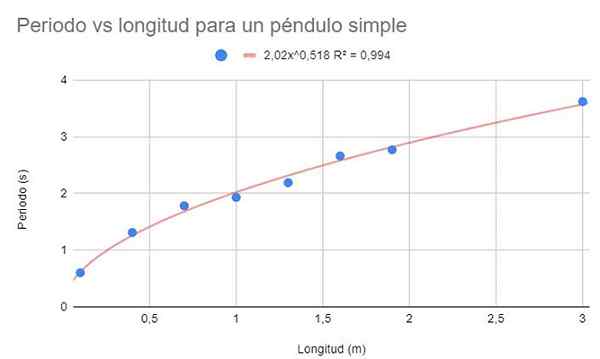Rysunek 3. Rozwiązanie graficzne ćwiczenia 2. Źródło: f. Zapata.

Pokaż także funkcję regulacji i jej współczynnik r -określenia².

Rozwiązanie

Potencjalna funkcja jest postaci f (x) = ax^B, gdzie A i B są stałe, które są określone metodą minimalną kwadratową.

Poprzednia rysunek pokazuje funkcję potencjalną i jej parametry, a także współczynnik określania o bardzo wysokiej wartości 99%. Zauważ, że dane podążają za krzywizną linii trendu.

Może ci służyć: zasada addytywna

- Przykład 3

Z tymi samymi danymi z przykładu 1 i przykładu 2, dokonaj drugiego stopnia wielomianowego. Pokaż wykres, wielomian regulacji i współczynnik określenia r² korespondent.

Rozwiązanie

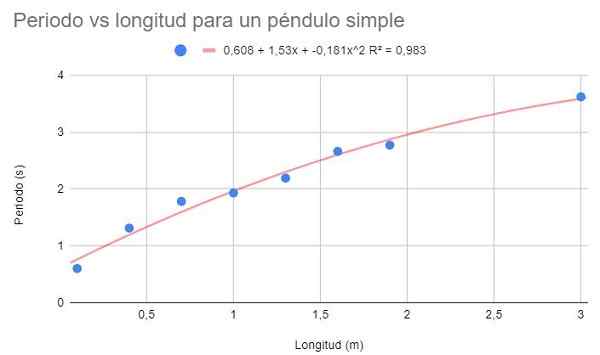Rysunek 4. Graphic Ćwiczenie 3. Źródło: f. Zapata.

W przypadku wielomianowej regulacji drugiego stopnia można zobaczyć linię trendu, która dobrze pasuje do krzywizny danych. Podobnie współczynnik determinacji znajduje się powyżej regulacji liniowej i poniżej regulacji potencjalnej.

Porównanie korekty

Spośród trzech pokazanych korekt, ten o wyższym współczynniku determinacji jest dostosowanie potencjału (przykład 2).

Potencjalne dostosowanie pokrywa się z fizyczną teorią wahadła, która, jak wiadomo, określa, że ​​okres wahadła jest proporcjonalny do pierwiastka kwadratowego o jego długości, będąc stałą proporcjonalności 2π /√g, gdzie g jest przyspieszeniem grawitacji.

Ten rodzaj potencjalnego dostosowania ma nie tylko najwyższy współczynnik determinacji, ale wykładnik i proporcjonalność stały z modelem fizycznym. 

Wnioski

-Dostosowanie regresji określa parametry funkcji, która ma na celu wyjaśnienie danych metodą minimalną kwadratową. Ta metoda polega na minimalizacji suma kwadratowej różnicy między wartością a regulacją a wartością Yi danych dla wartości xi danych. W ten sposób określane są parametry funkcji regulacji.

-Jak widzieliśmy, najczęstszą funkcją regulacji jest linia, ale nie jest to jedyna, ponieważ regulacje mogą być również wielokrotne, potencjalne, wykładnicze, logarytmy i inne. 

-W każdym razie współczynnik określenia zależy od danych i rodzaju dostosowania i wskazuje na dobroć zastosowanej korekty.

-Wreszcie współczynnik określenia wskazuje procent całkowitej zmienności między wartością a danymi w odniesieniu do wartości ŷ regulacji podanej x.

Bibliografia

1. González c. Statystyka ogólna. Odzyskane z: tarwi.La Molina.Edu.pe
2. IAC. Aragonese Institute of Health Sciences. Pobrano z: ICS-Aragon.com
3. Salazar c. i Castillo s. Podstawowe zasady statystyki. (2018). Źródło: DSPACE.Uce.Edu.Ec
4. Superprof. Współczynnik determinacji. Odzyskane z: Superprof.Jest
5. USAC. Podręcznik statystyki opisowej. (2011). Odzyskane z: statystyki.Inżynieria.USAC.Edu.Gt.
6. Wikipedia. Współczynnik determinacji. Odzyskane z: jest.Wikipedia.com.