Test Tukeya w tym, co jest, mistrzem, ćwiczenie rozwiązane

Test Tukeya Jest to metoda, której celem jest porównanie poszczególnych średnich z analizy wariancji kilku próbek poniżej.

Test, przedstawiony w 1949 roku przez Johna.W. Tukey, pozwala dostrzec, czy uzyskane wyniki są znacząco różne, czy nie. Jest również znany jako Tukey szczerze znacząca różnica test (Test HSD Tukeya za akronim w języku angielskim).

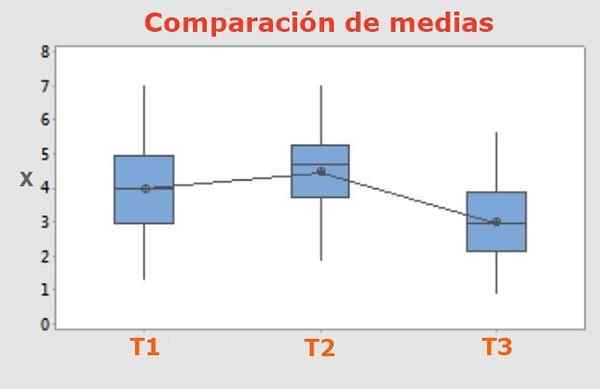
Rysunek 1. Test Tukeya pozwala dostrzec, czy różnice w wyniku między trzema lub więcej różnymi zabiegami zastosowały do ​​trzech lub więcej grup o równych cechach, mają znaczące i szczerze różne średnie wartości.

W eksperymentach, w których porównuje trzy lub więcej różnych zabiegów stosowanych do tej samej liczby próbek, konieczne jest rozróżnienie, czy wyniki są znacząco różne, czy nie.

Mówi się, że eksperyment jest zrównoważony, gdy rozmiar wszystkich próbek statystycznych jest taki sam w każdym zabiegu. Gdy rozmiar próbkowania jest inny dla każdego zabiegu, następuje niezrównoważony eksperyment.

Czasami nie wystarczy analizę wariancji (ANOVA), aby wiedzieć, czy w porównaniu różnych metod leczenia (lub eksperymentów) zastosowano do kilku próbek, które wypełniają hipotezę zerową (HO: „Wszystkie leczenie są takie same”), czy też przeciwne. spełnia alternatywną hipotezę (HA: „Przynajmniej jedno z zabiegów jest różne”).

Test Tukeya nie jest wyjątkowy, istnieje o wiele więcej dowodów na porównanie próbek, ale jest to jeden z najbardziej znanych i zastosowanych i zastosowanych.

[TOC]

Tabela komparatora i Tukeya

W zastosowaniu tego testu obliczana jest wartość W nazywany Komparator Tukeya którego definicja jest następująca:

W = Q √ (MSE /R)

Gdzie czynnik Q Jest uzyskiwany z tabeli (tabela Tukeya), która składa się z szeregów wartości Q Dla różnych zabiegów lub eksperymentów. Kolumny wskazują wartość współczynnika Q W różnych stopniach wolności. Zwykle dostępne tabele mają względne środki 0.05 i 0.01.

Może ci służyć: w oczekiwaniu na wiersz: wzór i równania, reprezentacja, przykłady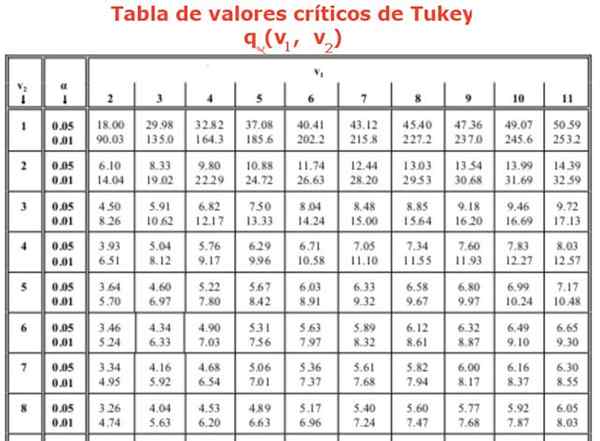

W tym wzorze, w pierścieniu kwadratowym, współczynnik MSE pojawia się (średni kwadrat błędu) podzielony przez r, co wskazuje na liczbę powtórzeń. MSE to liczba, która jest zwykle uzyskiwana z analizy wariancji (ANOVA).

Gdy różnica między dwoma średnimi wartościami przekracza wartość W (Komparator Tukeya), wówczas stwierdza się, że są to różne średnie, ale jeśli różnica jest mniejsza niż liczba Tukeya, to dwie próbki o statystycznie identycznej średniej wartości.

Liczba W jest również znana jako liczba HSD (szczerze znacząca różnica).

Ten jedyny numer komparatora można zastosować, jeśli liczba próbek zastosowanych do testu każdego zabiegu jest taka sama w każdym z nich.

Niezrównoważone eksperymenty

Kiedy z jakiegoś powodu rozmiar próbek jest różny w każdym zabiegu, aby porównać, wówczas procedura opisana powyżej różni się nieznacznie i jest znana jako Test Tukey-Kramer.

Teraz otrzymuje się liczbę W komparator dla każdej pary zabiegów Ja, J:

w (i, j) = q √ (½ mse /(ri +rj))

W tym wzorze współczynnik uzyskany z tabeli Tukeya. Wspomniany czynnik, który zależy od liczby zabiegów i stopni swobody błędu. R_Siema Jest to liczba powtórzeń w leczeniu I, a R, a R_J Jest to liczba powtórzeń w leczeniu J.

Przykładowy przypadek

Hodowca królików chce przeprowadzić wiarygodne badanie statystyczne, które wskazuje, który z czterech marek żywnościowych tubijących królików jest najbardziej skuteczny. W badaniu tworzy cztery grupy z sześcioma miesięcznymi królikami, które do tego czasu miały te same warunki żywnościowe.

Od eksperymentu do pierwszej grupy nazywa się A1, ponieważ będzie żywi się żywnością marki 1, podobnie jak grupa A2, A3 i A4. Stworzenie jest wykonane w miejscu, w którym rejestrowany jest przyrost masy ciała (w funtach) każdego okazu po miesiącu żywności z różnymi markami żywności, uzyskując następujące wyniki: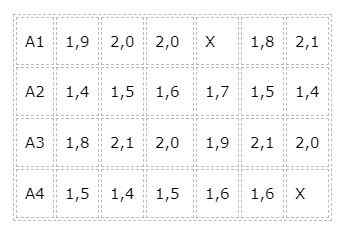Chociaż zaczęło się to od zrównoważonego eksperymentu, w tym sensie, że liczba królików, do których zastosowanie zostanie zastosowane, była taka sama, eksperymentu nie można było w ten sposób zakończyć.

Może ci służyć: negatywna homotecia

Przyczyną było to, że w grupach A1 i A4 miały miejsce ze względu na przyczyny, które nie można przypisać pożywienia, ponieważ jeden z królików został posiekany przez owada, aw drugim przypadku śmierć była z pewnością przyczyną wad wrodzonej wad. Tak aby grupy były niezrównoważone, a następnie konieczne jest zastosowanie testu Tukey-Kramer.

Ćwiczenie rozwiązane

Aby nie rozszerzyć zbyt dużych obliczeń, przypadek zrównoważonego eksperymentu zostanie potraktowany jako rozwiązanie ćwiczenia. Poniższe zostaną przejęte jako dane:

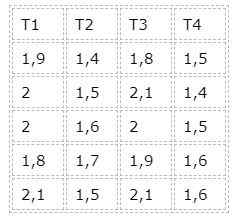
W takim przypadku istnieją cztery grupy odpowiadające czterem różnych zabiegach. Jednak obserwujemy, że wszystkie grupy mają taką samą liczbę danych, więc jest to wówczas przypadek zrównoważony.

Aby przeprowadzić analizę ANOVA, narzędzie włączone do arkusza kalkulacyjnego LibreOffice. Inne arkusze kalkulacyjne, takie jak Przewyższać Mają to narzędzie do analizy danych. Poniżej znajduje się tabela podsumowująca, która powstała po analizie wariancji (ANOVA):

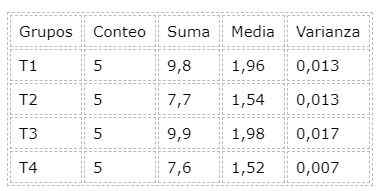
Z analizy wariancji istnieje również wartość p, która na przykład jest 2.24e-6 znacznie poniżej 0.05 poziomu istotności, co prowadzi bezpośrednio do odrzucenia hipotezy zerowej: wszystkie leczenie są równe. 

Oznacza to, że wśród zabiegów niektóre mają różne średnie wartości, ale musisz wiedzieć, jakie są znaczące i szczerze różne (HSD) od statystycznego punktu widzenia za pomocą testu Tukeya.

Aby znaleźć liczbę w lub jako liczbę HSD, wymaga również średniego kwadratu błędu MSE. Z analizy ANOVA uzyskuje się, że suma kwadratów w grupach wynosi SS = 0,2; A liczba stopni swobody w grupach wynosi df = 16 z tymi danymi, które możemy znaleźć MSE:

Może ci służyć: papomudas

MSE = SS/DF = 0,2/16 = 0,0125

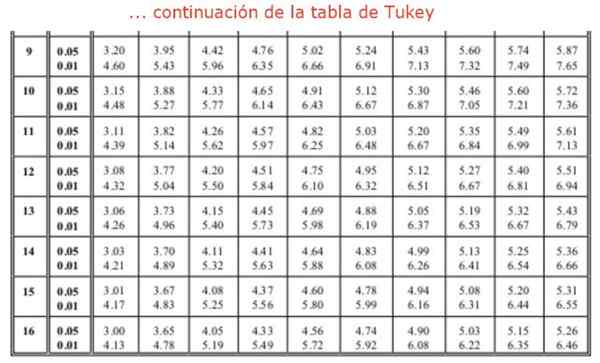
Wymagane jest również znalezienie czynnika Q z Tukeya, używając stołu. W kolumnie 4 poszukiwane jest 4 grupy lub zabiegi do porównania i rządu 16, ponieważ analiza ANOVA wykazała 16 stopni swobody w grupach. To prowadzi nas do wartości Q równej: Q = 4,33 odpowiadające znaczeniu 0,05 lub 95% niezawodności. Wreszcie znaleziono wartość „uczciwie znaczącej różnicy”:

W = hsd = Q √ (MSE /R) = 4,33 √ (0,0125 /5) = 0,2165

Aby wiedzieć, jakie są szczerze różne grupy lub zabiegi, musisz znać średnie każdego zabiegu:

Konieczne jest również znanie różnic między średnimi wartościami par zabiegów, co pokazano w poniższej tabeli:

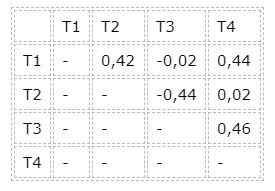Grupy T3 i T1, a także grupy T2 i T4, mają identyczne wyniki. Tak więc uczciwie różne grupy to grupy T1 i T2 lub T3 i T4, ponieważ różnica w ich średnich wartościach przekracza wartość HSM testu Tukeya.

Stwierdzono, że najlepsze zabiegi, jeśli chodzi o maksymalizację wyniku, to T1 lub T3, które są obojętne od statystycznego punktu widzenia. Aby wybrać między T1 i T3, należy szukać innych czynników poza analizą. Na przykład cena, dostępność itp.

Bibliografia

1. Cochran William i Cox Gertrude. 1974. Projekty eksperymentalne. Trillas. Meksyk. Trzeci przedruk. 661p.
2. Snedecor, G.W. I Cochran, w.G. 1980. Metody statystyczne. Siódmy edycja. Iowa, Iowa State University Press. 507p.
3. Steel, r.G.D. I Torrie, J.H. 1980. Zasady i procedury statystyki: podejście biometryczne (wydanie 2.). McGraw-Hill, Nowy Jork. 629p.
4. Tukey, J. W. 1949. Indywidualne porównywanie średnich w analizie wariancji. Biometrics, 5: 99-114.
5. Wikipedia. Test Tukeya. Źródło: w:.Wikipedia.com