Właściwości macierzy ortogonalnej, demonstracja, przykłady

Masz jeden Matryca ortogonalna Kiedy wspomniana macierz pomnożona przez jej transpozycję wyniki w macierzy tożsamości. Jeśli odwrotność macierzy jest równa transponowanej, oryginalna macierz jest ortogonalna.

Matryce ortogonalne są charakterystyczne, że liczba wierszy jest równa liczbie kolumn. Ponadto wektory rzędowe to wektory ortogonalne jednostkowe, a wysypka wektorów transponowanych.

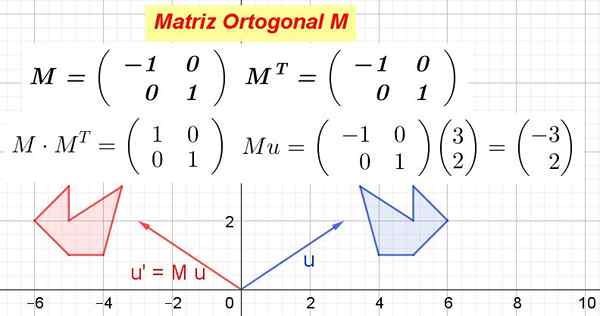Rysunek 1. Przykład macierzy ortogonalnej i sposób przekształcenia obiektów geometrycznych. (Przygotowane przez Ricardo Pérez)

Gdy macierz ortogonalna jest mnożona przez wektory przestrzeni wektorowej transformacja izometryczna, to znaczy transformacja, która nie zmienia odległości i zachowuje kąty.

Typowym przedstawicielem macierzy ortogonalnych są Matryce obrotowe. Nazywane są transformacje macierzy ortogonalnych na przestrzeni wektorowej Transformacje ortogonalne.

Geometryczne transformacje obrotu i odbicie punktów reprezentowane przez jego wektory kartezjańskie są wykonywane przez zastosowanie matryc ortogonalnych na oryginalne wektory w celu uzyskania współrzędnych transformowanych wektorów. Z tego powodu macierze ortogonalne są szeroko stosowane w obliczeniowym przetwarzaniu graficznym.

[TOC]

Nieruchomości

Tablica M Jest ortogonalny, jeśli jest pomnożony przez jego transponię M^T Macierz tożsamości powoduje Siema. Podobnie produkt transpozycji macierzy ortogonalnej przez oryginalną matrycę macierzy tożsamości:

M m^T = M^T M = i

W wyniku poprzedniego stwierdzenia transponowanie macierzy ortogonalnej jest równa jej odwrotnej matrycy:

M^T = M^-1.

Zestaw macierzy wymiarów ortogonalnych n x n Tworzą grupę ortogonalną Lub (n). I podzbiór Lub (n) macierzy ortogonalnych z określeniem +1 Specjalne macierze grupy ITS (N). Macierze grupy Twój (n) Są to matryce, które wytwarzają liniowe transformacje obrotu, znane również jako Grupa rotacji.

Demonstracja

Wykazamy, że matryca jest ortogonalna, jeśli i tylko wtedy, gdy wektory wiersza (lub wektory kolumny) są do siebie ortogonalne i normy 1.

Może ci służyć: twierdzenie Bayesa

Załóżmy, że szeregi macierzy ortogonalnej n x n są wektorami o wymiarach n. Jeśli jest oznaczony przez v1, v2,.. ., vN N wektory są spełnione:

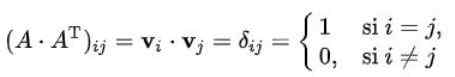
Gdzie jest oczywiste, że zestaw wektorów rzędowych jest zestawem wektorów ortogonalnych z normą.

Przykłady

Przykład 1

Pokaż, że macierz 2 x 2, którą wektor ma w swoim pierwszym rzędzie V1= (-1 0) i w drugim rzędzie wektor V2= (0 1) jest macierzą ortogonalną.

Rozwiązanie: Matryca jest zbudowana M a jego transpozycja jest obliczana M^T:

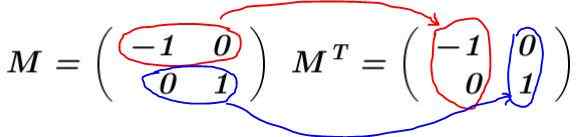
W tym przykładzie macierz M Jest to transponowany samochód, to znaczy, że matryca i jej transpozycja są identyczne. Mnoży się M za jego transpozycję M^T:

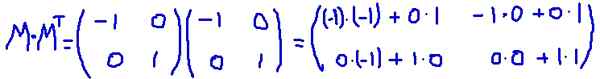
Jest to zweryfikowane M M^T Jest równy matrycy tożsamości:

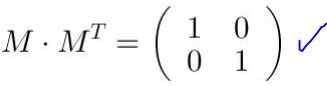
Kiedy macierz M Jest mnożony przez współrzędne wektora lub punkt, uzyskuje się nowe współrzędne, które odpowiadają transformacji, którą ma matrycę na wektorze lub punkcie.

Rysunek 1 pokazuje, jak M Przekształca wektor Lub W Lub' A także jak M Przekształć niebieski wielokąt w czerwony wielokąt. Jak M Jest ortogonalny, jest to transformacja ortogonalna, która zachowuje odległości i kąty.

Przykład 2

Załóżmy, że masz matrycę 2 x 2 zdefiniowaną w reaiS podanym przez następujące wyrażenie:

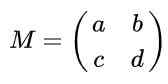
Znajdź rzeczywiste wartości Do, B, C I D tak że macierz M Być matrycą ortogonalną.

Rozwiązanie: Z definicji macierz jest ortogonalna, jeśli pomnożona przez jej transponię jest uzyskiwana w wyniku macierzy tożsamości. Pamiętając, że transponowana macierz jest uzyskiwana z oryginału, wymiana wierszy według kolumn jest następującą równością:

Może ci służyć: domena i sprzeczność funkcji (z przykładami)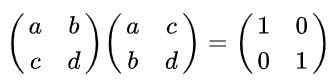

Wykonanie mnożenia macierzy to:

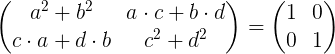
Wyrównując elementy lewej macierzy z elementami macierzy tożsamości po prawej, otrzymujemy układ czterech równań z czterema niewiadomymi A, B, C i D.

Proponujemy następujące wyrażenia A, B, C i D oparte na przyczynach trygonometrycznych zatok i cosinus:

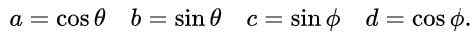
Z tą propozycją i ze względu na podstawową tożsamość trygonometryczną pierwsze i trzecie równanie w równości elementów macierzy jest automatycznie spełnione. Trzecie i czwarte równanie są takie same, a w równości macierzy po wymianie proponowanych wartości jest takie:

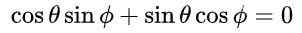
co prowadzi do następującego rozwiązania:

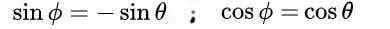
Na koniec uzyskano następujące rozwiązania dla macierzy ortogonalnej M:

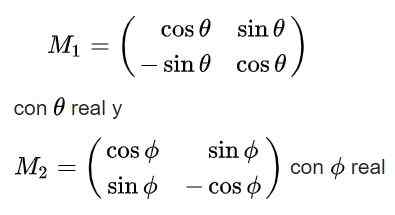
Zauważ, że pierwsze z roztworów ma determinant +1, więc należy do jego grupy (2), podczas gdy drugie rozwiązanie ma determinant -1 i dlatego nie należy do tej grupy.

Przykład 3

Biorąc pod uwagę następującą matrycę, znajdź wartości A i B, które mają macierz ortogonalną.

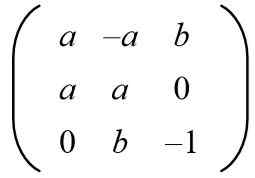
Rozwiązanie: Aby dana matryca była ortogonalna, produkt z jej transpozycją musi być macierz tożsamości. Następnie wytwarzany jest produkt macierzy matrycy podanej z jej transponowaną matrycą: dając następujący wynik:

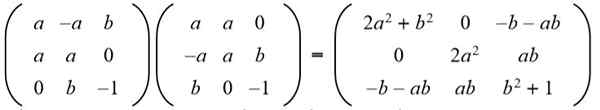
Następnie wynik jest dopasowany do macierzy tożsamości 3 x 3:

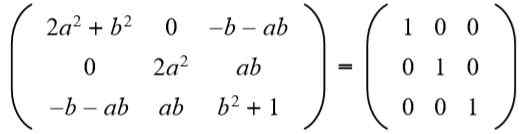
W drugim wierszu masz trzecią kolumnę (A B = 0), Ale Do Nie może być zero, ponieważ jeśli tak, równość elementów drugiego rzędu i drugiej kolumny nie zostanie spełniona. Wtedy koniecznie B = 0. Zastąpienie B Dla wartości 0 mamy:

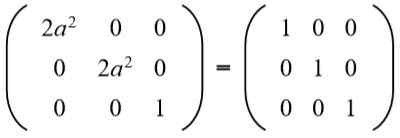
Następnie równanie jest rozwiązane: 2a^2 = 1, którego rozwiązania to: +½√2 i -½√2.

Może ci służyć: rodzaje kątów, cechy i przykłady

Przyjmując pozytywne rozwiązanie do Do Powoduje to następującą matrycę ortogonalną:

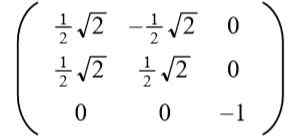
Czytelnik może łatwo sprawdzić, czy wektory wierszy (a także wektory kolumn) są ortogonalne i jednostki, to znaczy ortonormal.

Przykład 4

Wykazać, że macierz DO których rzędy są V1 = (0, -1 0), V2 = (1, 0, 0) I V3 = (0 0-1) Jest to macierz ortogonalna. Dodatkowo odkryj, jak przekształcane są wektory podstawy kanonicznej I J K Do wektorów U1, U2 I U3.

Rozwiązanie: Należy pamiętać, że element (i, j) macierzy pomnożony przez jego transpozycję jest produktem skalarnym wektora rzędu (i) przez kolumnę (j) transpozy. Ponadto ten produkt jest równy delcie Kroneckera na wypadek, gdyby matryca była ortogonalna:

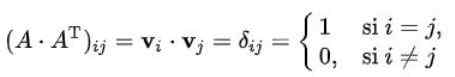
W naszym przypadku jest tak:

V1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • v2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

Z tym, co pokazano, że jest to matryca ortogonalna.

Oprócz u1 = a i = (0, 1, 0); U2 = j = (-1, 0, 0) i wreszcie U3 = a k = (0, 0, -1)

Bibliografia

1. Anthony Nicolaides (1994) Determinanty i macierze. Pokrywanie publikacji.
2. Birkhoff i Maclane. (1980). Modern Algebra, Ed. Vicens-Vives, Madryt.
3. Casteleiro Villalba m.  (2004) Wprowadzenie do algebry liniowej. ESIC EDYTORIAL.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
6. Richard J. Brown (2012) 30-sekundowe matematyki: 50 najbardziej ekspandujących teorie w matematyce. Ivy Press Limited.
7. Wikipedia. Matryca ortogonalna. Odzyskane z: jest.Wikipedia.com
8. Wikipedia. Matryca ortogonalna. Źródło: w:.Wikipedia.com