Kepler Laws Wyjaśnienie, ćwiczenia, eksperyment

Prawa Keplera O ruchu planetarnym sformułował niemiecki astronom Johannes Kepler (1571-1630). Kepler wydedukował je na podstawie pracy jego nauczyciela duńskiego astronomu Tycho Brahe (1546-1601).

Brahe starannie skompilował dane z ruchów planetarnych przez ponad 20 lat, z zaskakującą dokładnością i dokładnością, jeśli zostanie to uwzględnione, że w momencie, gdy teleskop nie został jeszcze wynaleziony. Ważność twoich danych jest nadal ważna.

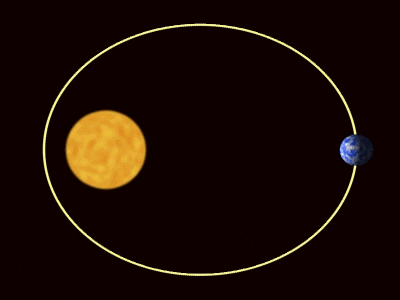Rysunek 1. Orbity planet zgodnie z prawami Keplera. Źródło: Wikimedia Commons. Willow/cc przez (https: // creativeCommons.Org/licencje/według/3.0)

[TOC]

3 prawa Keplera

Prawa Keplera ustanawiają:

-Pierwsze prawo: Wszystkie planety opisują orbity eliptyczne ze słońcem w jednym z reflektorów.

-Drugie prawo lub prawo tego samego: Linia skierowana ze Słońca na dowolną planetę (radio ogniskowe), zamiataj równe obszary w równych czasach.

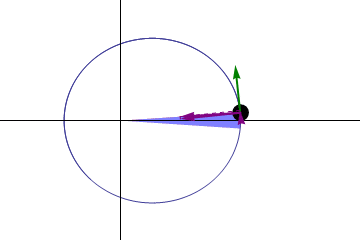Rysunek 2. Prawo obszarów. Źródło: Wikimedia Commons. Gonfer/cc by-sa (https: // creativeCommons.Org/licencje/by-sa/3.0)

-Trzecie prawo: Plac czasowy, który zajmuje dowolną planety orbital wokół słońca, jest proporcjonalny do sześcianu średniej odległości od słońca.

Być T Wspomniany czas, zadzwonił Okres orbitalny, I R Zatem średnia odległość:

T² jest proporcjonalny do r³

T = k r³

Oznacza to, że iloraz T²/ R³ Tak samo jest dla wszystkich planet, co umożliwia obliczenie promienia orbitalnego, jeśli znany jest okres orbity.

Gdy T Jest wyrażany w latach i R W jednostkach astronomicznych ua*stała proporcjonalności jest warta k = 1:

T²= r³

*Jednostka astronomiczna jest równoważna 150 milionów kilometrów, czyli średniej odległości między Ziemią a Słońcem. Okres orbitalny ziemi wynosi 1 rok.

Powszechne prawo grawitacyjne i trzecie prawo Keplera

Uniwersalne prawo grawitacyjne określa, że ​​wielkość siły przyciągania grawitacyjnego między dwoma obiektami masy M I M odpowiednio, których centra są oddzielne odległość R, Jest podany przez:

F = g mm /r²

G jest uniwersalną stałą grawitacji, a jej wartość wynosi g = 6.674 x 10 ^-jedenaście N.M²/kg² .

Teraz orbity planet są eliptyczne z bardzo małą ekscentrycznością.

Oznacza to, że orbita nie odsuwa się zbyt wiele od koła, z wyjątkiem niektórych przypadków, takich jak krasnolud. Jeśli przybliżamy orbity do postaci okrągłej, przyspieszenie ruchu planety wynosi:

Do_C = v²/R

Biorąc pod uwagę F = ma, Posiadać:

G mm /r² = m.v²/R

Tutaj v Jest to liniowa prędkość planety wokół słońca, statyczne i masowe założenie M, Podczas gdy planeta jest M. Więc:

Może ci służyć: znaczące liczby: zasady, przykłady, rozwiązane ćwiczenia

To wyjaśnia, że ​​planety najdalej od słońca mają niższą prędkość orbity, ponieważ zależy to od 1/√r.

Jako odległość, którą porusza planeta, jest w przybliżeniu długość obwodu: l = 2πr i zajmuje równy czas t, okres orbitalny, jest uzyskiwana:

V = 2πr /t

Wyrównanie obu wyrażeń dla v uzyskuje się prawidłowe wyrażenie dla t², Kwadrat okresu orbitalnego:

I jest to dokładnie trzecie prawo Keplera, ponieważ w tym wyrażeniu nawias 4π² /GM Dlatego jest stałe T² jest proporcjonalny do odległości R podniesiony do kostki.

Ostateczne równanie dla okresu orbitalnego uzyskuje się poprzez wyodrębnienie pierwiastka kwadratowego:

Obliczanie masy słońca

Ile kosztuje masa słońca? Możliwe jest dowiedzieć się przez to równanie. Wiemy, że okres orbity ziemi wynosi jeden rok, a promień orbity wynosi 1 UA, co odpowiada 150 milionom kilometrów, więc mamy wszystkie niezbędne dane.

W naszym poprzednim równaniu jasne M, ale nie przed przekształceniem wszystkich wartości na międzynarodowy system jednostek, jeśli:

1 rok = 3.16 x 10⁷ sekundy.

1 UA = 150 milionów km = 1.5 x10^jedenaście M.

A zastępując dane w równaniu, uzyskujemy dość udane oszacowanie Słońca Słońca w 2.0 x 10 ³⁰ kg.

Ćwiczenia

Chociaż Kepler miał na myśli tylko planety, kiedy czerpał swoje słynne prawa, są one również ważne dla ruchu satelitów i innych ciał układu słonecznego, jak zobaczymy następne.

- Ćwiczenie 1

Wiedząc, że orbita Jowisza wynosi 5.19 razy większy niż na Ziemi, znajdź okres orbitalny Jowisza.

Rozwiązanie

Zgodnie z definicją jednostki astronomicznej Jowisz pochodzi ze Słońca 5.19 UA, zatem zgodnie z trzecim prawem Keplera:

T²= r³= (5.19)³ lata

Dlatego T = (5.19)^3/2  lata = 11.8 lat

- Ćwiczenie 2

Halley Comet odwiedza słońce co 75.3 lata. Znajdować:

a) Główny pół -kielisz się orbity.

b) miara apelium, jeśli peryhelium mierzy 0.568 UA.

Rozwiązanie

Halley Comet odwiedza słońce co 75.3 lata. Znajdować:

a) Główny pół -kielisz się orbity.

b) miara apelium, jeśli peryhelium mierzy 0.568 UA.

Rozwiązanie

Kiedy planeta lub jakakolwiek inna gwiazda znajduje się najbliżej słońca, mówi się, że jest w Perihelio, A kiedy jest dalej, w Aphelion. W szczególnym przypadku okrągłej orbity R w trzecim prawie Keplera jest promieniem orbity.

Może ci służyć: stałe antoine: wzory, równania, przykłady

Jednak na orbicie eliptycznej ciało niebiańskie jest mniej więcej z dala od słońca, będąc półmokiem „a” średnią między aprootess a peryhelium:

Rysunek 3. Aflio i Perihelio. Źródło: Wikimedia Commons. Pearson Scott Foesman / Public Domena

Dlatego zastępujemy R za pomocą trzeciego prawa Keplera, które wynika dla Halleya w:

T²= a³→ a = (t)²³ → A = (75.3) ²³ UA = 17.832 UA

Rozwiązanie b

A = ½ (perihelio + apelio)

17.832 = ½ (0.568+ aflio) → aflio = 2 x 17.832 - 0.568 UA = 35.10 UA.

Eksperyment

Przeanalizuj ruch planet wymaga tygodni, miesięcy, a nawet lat starannej obserwacji i rejestracji. Ale w laboratorium można przeprowadzić bardzo prosty eksperyment, aby udowodnić, że prawo Keplera jest spełnione.

W tym celu wymagany jest system fizyczny, w którym siła rządząca ruchem jest centralny, wystarczający warunek, aby prawo obszarów zostało spełnione. Taki system składa się z masy przywiązanej do długiej liny, z drugim końcem stałego wątku do wsparcia.

Ciasto oddziela niewielki kąt jego pozycji równowagi i jest drukowane lekkim impulsem, tak że wykonuje owalny (prawie eliptyczny) ruch na płaszczyźnie poziomej, jakby była to planeta wokół słońca.

Na krzywej opisanej przez wahadło możemy udowodnić, że w równych czasach zamiata równe obszary, tak:

-Rozważamy radia wektorowe, od środka przyciągania (początkowe punkt równowagi) do położenia masy.

-I my Barmos między dwoma kolejnymi momentami o równym czasie, w dwóch różnych obszarach ruchu.

Im dłuższy gwint wahadłowy i niższy kąt, który odjeżdża od pionowej, siła regeneracyjna netto będzie bardziej pozioma, a symulacja przypomina przypadek ruchu z siłą centralną w płaszczyźnie.

Następnie opisany owalny zbliża się do elipsy, na przykład ta, którą podróżują planety.

Materiały

-Niewykłacalny wątek

-1 ciasto lub metalowa kulka pomalowana na biało, która działa jak wahadło soczewicy

-Linijka

-Przenośnik

-Kamera z obrazem z automatycznym dyskem stroboskopowym

-Wsparcie

-Dwa źródła oświetlenia

-Arkusz papieru lub czarny karton

Może ci służyć: Big Crunch Theory: History, Zasady, dane za i przeciw

Procedura

Montaż postaci jest potrzebny do robienia zdjęć wielu błysków wahadła, gdy jego trajektoria następuje. Aby to zrobić, musisz umieścić aparat tuż nad wahadłem i automatycznym albumem stroboskopowym przed obiektywem.

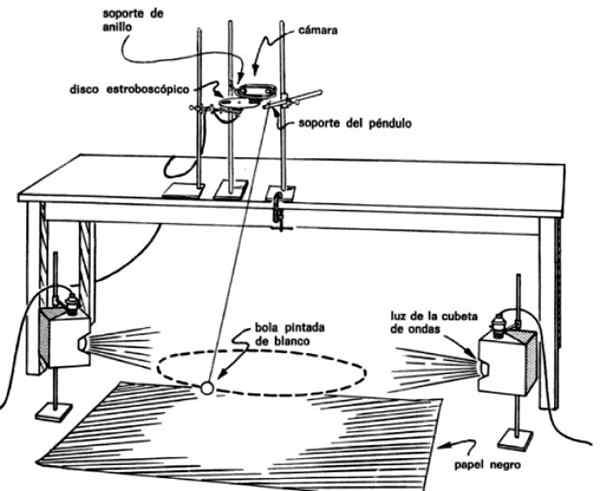Rysunek 4. Zespół wahadła, aby sprawdzić, czy w równych czasach zamiata równe obszary. Źródło: PSSC Laboratory Guide.

W ten sposób obrazy są uzyskiwane w regularnych odstępach czasu wahadła, na przykład co 0.1 lub co 0.2 sekundy, co pozwala poznać czas przejścia z jednego punktu do drugiego.

Musisz także wygodnie oświetlić masę wahadła, umieszczając światła po obu stronach. Soczewica musi być pomalowana na biało, aby poprawić kontrast na tle, który składa się z rozszerzonego czarnego papieru na ziemi.

Teraz musisz sprawdzić, czy wahadło zamiatają równe obszary w równych czasach. W tym celu wybrano przedział czasowy, a punkty zajmowane przez wahadło we wspomnianym odstępie są oznaczone na papierze.

Na obrazie linia jest pobierana od środka owalnego do tych punktów, więc będziemy mieć pierwszy z obszarów zmiecionych przez wahadło, który jest w przybliżeniu sektorem eliptycznym, jak ten pokazany poniżej:

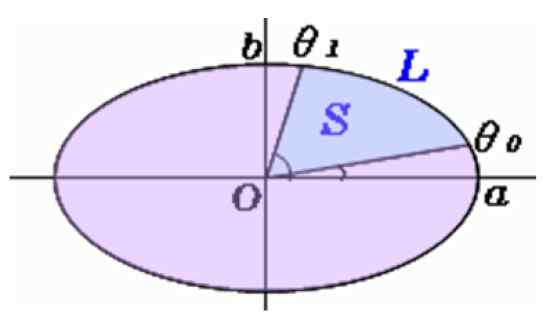Rysunek 5. Obszar sektora eliptycznego. Źródło: f. Zapata.

Obliczanie obszaru sekcji eliptycznej

Kąty są mierzone za pomocą przenośnika θ_albo I θ₁, A ta formuła służy do znalezienia S, obszar sektora eliptycznego:

S = f (θ₁) - f (θ_albo)

Z F (θ) podane przez:

Zauważ, że Do I B Są odpowiednio półsenży odpowiednio i mniejszymi. Czytelnik powinien jedynie starannie zmierzyć półsek i kąty, ponieważ istnieją kalkulatory online, aby łatwo ocenić to wyrażenie.

Jeśli jednak nalegasz na ręcznie dokonanie obliczeń, musisz pamiętać, że kąt θ jest mierzony w stopniach, ale w momencie wprowadzenia danych do kalkulatora wartości muszą być wyrażone w promieniach.

Następnie musisz zaznaczyć kolejną parę punktów, w których wahadło zainwestowało w tym samym przedziale czasowym i narysować odpowiedni obszar, obliczając jego wartość z tą samą procedurą.

Weryfikacja prawa równych obszarów

Wreszcie pozostaje w sprawie sprawdzenia, czy prawo obszarów jest spełnione, to znaczy, że w równych czasach równe obszary są zamiatanie.

Czy wyniki nieco odbiegają od oczekiwanych? Musisz pamiętać, że wszystkim miarom towarzyszy ich odpowiedni błąd eksperymentalny.

Bibliografia

1. Kalkulator online Keisan. Obszar kalkulatora sektora eliptycznego. Odzyskany z: Keisan.Casio.com.
2. Opentax. Prawo Keplera ruchu planetarnego. Źródło: OpenStax.org.
3. PSSC. Fizyka laboratoryjna. Redakcja Reverted. Odzyskane z: książki.Google.współ.
4. Palen, s. 2002. Astronomia. Seria Schaum. McGraw Hill.
5. Pérez r. Prosty system z siłą centralną. Odzyskane z: Francessphysics.Blogspot.com
6. Stern, d. Trzy prawa Keplera ruchu planetarnego. Odzyskany z: phy6.org.