De Morgan Prawa

Wyjaśniamy, jakie są prawa Morgana, pokazujemy je i stawiamy przykłady

Rysunek 1.- Matematyk Augusta z Morgan (1806–1871) i jego prawa logiki propozycyjnej. Źródło: f. Zapata.

Jakie są prawa de Morgana?

Prawo de Morgana to dwa logiczne prawa należące do logiki zdań sformułowanych przez angielskiego matematyka Augematyka Morgan (1806–1871). Ustalają następujące w odniesieniu do złożonej logicznej propozycji:

1. Przeciwieństwo koniunkcji jest równoważne z rozłączeniem utworzonym z przeciwieństwami lub zaprzeczaniem propozycji, które składają się.
2. Odmowa rozłączenia można wyrazić jako koniunkcja złożona z przeciwieństw lub zaprzeczenia propozycji zaangażowanych w rozłączenie.

W notacji logiki propozycyjnej prawa de Morgana są wyrażane w zwarty i bardziej formalny sposób:

1. ∼ (p ∧ q) ⇔ ∼p ∨q
2. ∼ (p ∨ q) ⇔ ∼p ∧q

Te przepisy wyrażają to, że albo w odmowie połączenia lub rozbieżności, wynik jest równoważny odmawianiu każdej z uczestniczących propozycji osobno i inwestowanie złącza, które je łączy.

Aby lepiej zrozumieć prawa de Morgana, konieczne jest przeglądanie znaczenia propozycji i symboli używanych w logice propozycyjnej, aby zobaczyć, w jaki sposób te przepisy są wygodnie stosowane.

Notacja logiczna

Podstawowym narzędziem logiki propozycyjnej są propozycje. Logiczna propozycja to stwierdzenie, które przyznaje prawdziwa wartość, Czy to prawda, czy fałszywa, ale nie oba jednocześnie. W tym nie jest dozwolona dwuznaczność, to znaczy nie ma wątpliwości.

Propozycja jest oznaczona małymi literami, jak w następujących przykładach:

• P: Meksyk jest stolicą Meksyku (prawda).
• P: Uzyskuje się 2 i 3, 4 (false).
• Odp.: Wszystkie ssaki są zwierzętami lądowymi (fałszywe).

Może ci służyć: heptagon

Istnieją również bardziej złożone propozycje, które są ustrukturyzowane dzięki zastosowaniu prostych propozycji, takich jak te:

• P: Carlos pójdzie do kina, jeśli nie padnie.
• P: Ana jest chemikiem lub biologiem morskim.
• Odp.: Juan idzie na obiad lub Pedro zobaczy grę w telewizji.

Logiczne złącza

Logiczne złącza to symbole używane do łączenia prostych propozycji, a tym samym budowania bardziej złożonych propozycji. W logice propozycyjnej każdy z nich ma szczególne znaczenie.

Najczęściej używanymi złączami są połączenie, rozłączenie, wyłączne rozłączenie, zaprzeczenie, warunkowość i dwukrotność.

Spójnik

Koniunkcja jest oznaczona odwróconą literem „V”. Złożona propozycja poprzez koniunkcję jest symbolizowana p ∧ q, jak następuje:

• P ∧ P: Meksyk jest stolicą Meksyku i jest w Ameryce Północnej.

Łatwo jest tutaj zidentyfikować, że P to „Meksyk miasto jest stolicą Meksyku”, a Q jest „w Ameryce Północnej”.

Dysjunkcja

Wyróżnia się dwa rodzaje rozbieżności: słabe i wyłączne. A słabe rozłączenie Jest symbolizowany przez ∨ i w notacji logicznej byłoby to p ∨ q. Przykład tego rodzaju rozbieżności jest:

• P ∨ Q: Juan jest piłkarzem lub Juan to tenisista.

Zamiast tego Wyłączenie wykluczającego Symbolizuje go znak ⊻ i oznacza, że ​​jedna z propozycji należy wykluczyć na przykład:

P ⊻ P: Alicia ma 20 lat lub Alicia ma 22 lata.

Różnica między obiema typami jest jasna, w wyłącznym rozłączeniu, jedna z propozycji jest wykluczona, ponieważ jeśli Alicia ma 20 lat, nie może mieć 22 lat i odwrotnie. Z drugiej strony, w słabym rozłączeniu, Juan może być jednocześnie piłkarzem i tenisistą.

Odmowa

Umieszczając symbol ∼ propozycja, odmawia się tego, jak w:

• P: ∼ (Veracruz jest stolicą Meksyku).

To jest czytane jako „Veracruz nie jest stolicą Meksyku”. Inne sposoby wyrażania zaprzeczenia, oprócz „nie”, są przez frazy takie jak „jest fałszywe”, „to kłamstwo” i „To nieprawda”.

Może ci służyć: interpolacja liniowa

Warunkowanie

Są to złożone propozycje, które zwykle używają słów „tak” i „Następnie ...”, aby połączyć dwie propozycje, w których istnieją warunkowe lub implikacja. Część propozycji zapisanej natychmiast po „tak” jest poprzednik fala hipoteza propozycji i tego, co jest po terminu „wtedy” jest wniosek albo następnik.

Symbkiem użytym do warunkowania jest strzałka od lewej do prawej „→”, dlatego warunkowość między dwiema propozycjami jest reprezentowana jako p → q, którą można odczytać jako „jeśli p, to q”. Na przykład:

P → P: Jeśli pada deszcz po południu, nie będę grać w tenisa.

Dwuprzecjaowość

W tego typu propozycji używa się wyrażenia „tak, i tylko wtedy”, aby połączyć dwie propozycje, zwane pierwszym i drugim elementem dwuosobowym. Zastosowanym symbolem jest strzałka dwukierunkowa „↔”.

Dwie propozycje połączone przez „tak i tylko wtedy, gdy” są odpowiednio wywoływane Pierwszy I drugi członek a dwuprzewaniowość dwóch propozycji p i q pozostaje jako p ↔ q. Na przykład:

P ↔ P: Maria lubi jeździć na rowerze, jeśli i tylko wtedy, gdy dzień jest słoneczny.

Demonstracja praw de Morgana

Prawo de Morgana są częścią logicznych równoważności i można je wykazać za pomocą tabel prawdy, które są używane do znania prawdy (prawdziwej lub fałszywej) wartości propozycji.

Ponieważ koniunkcja jest prawdziwa tylko wtedy, gdy P i Q są prawdziwe, jego tabela prawdy jest:

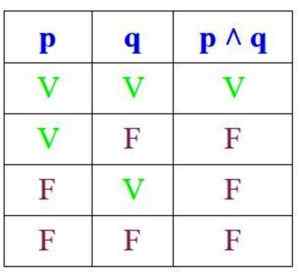
Z drugiej strony, w rozbieżności, propozycja jest prawdziwa, jeśli P i Q są prawdziwe lub jeśli przynajmniej jeden z nich jest, ale jest fałszywy, jeśli oba są:

Może ci służyć: permutacje bez powtórzeń: formuły, demonstracja, ćwiczenia, przykłady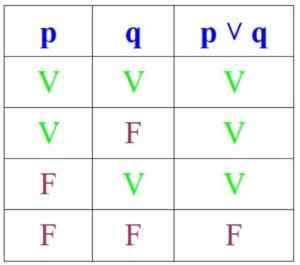

Teraz zaprzeczenie przekształca prawdę w fałszywe i odwrotnie. W tym przypadku wartości prawdy ∼ (p ∧ q) i ∼ (p ∨ q) są przeciwieństwem wartości prawdy (p ∧ q) i (p ∨ q):

I należy zweryfikować, że wyniki te są uzyskiwane podczas wykonywania odpowiednich tabel prawdy (∼ p ˅ ∼ q) i (∼ p ˄ ∼ q):

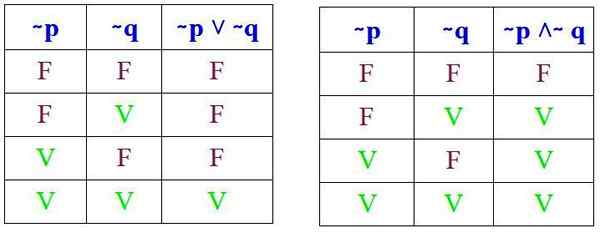
I rzeczywiście, porównując odpowiednie tabele prawdy, obserwuje się, że prawa de Morgana są spełnione. Teraz będą widoczne dwa przykłady jego wniosku.

Rozwiązany przykład 1

Zastosuj prawa de Morgana, aby znaleźć równoważną ekspresję: ∼ (∼p ˅ ∼q)

• Rozwiązanie

Dane wyrażenie jest porównywane ∼ (∼p ˅ ∼Q) z prawem Morgana:

∼ (p ∨ q) ⇔ ∼p ∧q

I obserwuje się, że zaprzeczenie jest już poza nawiasem w obu przypadkach, dlatego przestrzegane są instrukcje prawa: odmawia ∼p, zaprzecza ∼q, a złącze jest zmieniane:

∼ (∼p ˅ ∼Q) ⇔ ∼ (∼p) ∧ ∼ (∼Q) ⇔ p ∧ q

Rozwiązany przykład 2

Określ równoważną ekspresję ∼ [∼p ˄ ∼ (∼Q)] ≡

• Rozwiązanie

Po pierwsze, zaprzeczenie ∼Q jest uproszczone:

∼ [∼p ˄ ∼ (∼Q)] ⇔ ∼ [∼p ˄ q]

Ponieważ poza nawiasem jest już zaprzeczenie, wynikowe wyrażenie jest porównywane z prawem Morgana: ∼ (p ∧ q) ⇔ ∼p ∨q

Aby rozwiązać ∼ [∼p ˄ q], musisz zaprzeczyć ∼p, odmówić Q i zmienić złącze:

∼ [∼p ˄ q] ⇔ (∼p) ∨ ∼Q ⇔ p ˅ ∼Q

Bibliografia

1. Becerra, J.M.  Unam Logic Notes.
2. Genialny. Z praw Morgana. Odzyskane od: genialne.org.
3. Samouczki elektroniczne. Przez twierdzenie Morgana. Odzyskane z: elektroniki-tormales.WS.
4. López, f. Wprowadzenie do logiki matematycznej. Odzyskane z: YouTube.com
5. Muñoz, c. Wprowadzenie do logiki. Źródło: strony internetowe.UCM.Jest.