Formuły prawa Hooke, przykłady, aplikacje, ćwiczenia

Prawo Hooke wskazuje, że deformacja doświadczana przez obiekt sprężysty jest wprost proporcjonalny do przyłożonej siły na nim. Stała proporcjonalności zależy od natury obiektu, jego geometrii i materiału, z którym jest wytwarzany.

Wszystkie materiały mają elastyczne właściwości w większym lub mniejszym stopniu, więc są one zgodne z prawem Hooke, ilekroć wracają do pierwotnych wymiarów, gdy siła się ustanie. Sprężyny elastyczne i dziąsła są dobrymi przykładami obiektów, które są zgodne z prawem Hooke, ale podobnie jak stalowe kabiny, które są częścią mostu.

Rysunek 1. Prawo Hooke na wiosnę

Biorąc jako przykład sprężynę lub dok, aby utrzymać ją rozciągniętą lub ściśniętą, konieczne jest zastosowanie siły, której wielkość jest f. Zgodnie z prawem Hooke'a wiosna doświadczy deformacji X:

F ∝ x

Stała proporcjonalności, która jest wiosną, nazywa się Sztywność wiosenna, Dlatego jest oznaczony jako k:

F = k⋅x

W jednostkach systemu międzynarodowego siły pojawiają się w Newton (N) i deformacji w metrach (M). Dlatego stała sprężyna ma jednostki N/M. Stała sprężyna reprezentuje siłę, którą należy zastosować, aby odkształcić ją w długości 1 m.

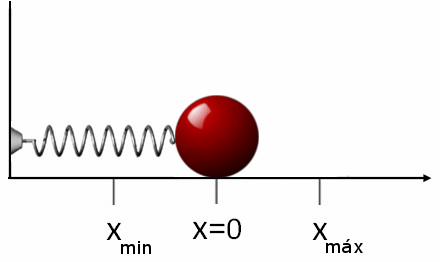Rysunek 2. Po rozciągnięciu sprężyny siła wywierana na obiekt jest przeciwna. To samo dzieje się, jeśli sprężyna się kurczy, w tym przypadku napędza obiekt w przeciwnym znaczeniu. Źródło: Wikimedia Commons.

Jeśli po rozciągnięciu lub ściskaniu sprężyny zostanie zwolniony, porusza się w przeciwnym kierunku do przyłożonej siły. Oznacza to, że jeśli go rozciągniemy, jest kompresowany i odwrotnie. Dlatego Force F_R To Wiosenne ćwiczenia Jest:

F_R = -K⋅x

Znak ujemny wskazuje, co się mówi: że siła sprzeciwia się wysiedleniu, więc siła ta jest znana jako Siła odbudowująca.

[TOC]

Wzór i równania

Związek między siłą a wysiedleniem na wiosnę został odkryty przez Roberta Hooke'a (1635-1703), godnego znaczącego angielskiego fizyka i znanego z jego rywalizacji z Izaakiem Newtonem. Hooke był wszechstronnym naukowcem, który z powodzeniem zajmował się różnymi dziedzinami nauki: mechanika, biologia, astronomia i architektura.

Rysunek 3. Angielski fizyk Robert Hooke, który nie zna portretów tamtych czasów. Jest to rekonstrukcja wykonana przez artystę Rity Gerer w 2004 r. Poprzez opisy pozostawione przez tych, którzy poznali naukowca. Źródło: Wikimedia Commons. Rita Greer / Fal.

Hooke zdał sobie sprawę, że jeśli siła nałożona na molo nie jest bardzo duża, dok jest proporcjonalnie deforma.

Może ci służyć: magnetosfera Ziemi: Charakterystyka, struktura, gazy

W ten sposób prawo Hooke graficznie ma kształt linii prostej, której nachylenie jest stałą sprężyny. Poniższy obraz pokazuje siłę wywieraną na sprężynę, aby ją rozciągnąć - lub ściskając - w zależności od pozycji X. Zauważ, że siła nie zależy od naturalnej długości sprężyny, ale od jej przemieszczenia.

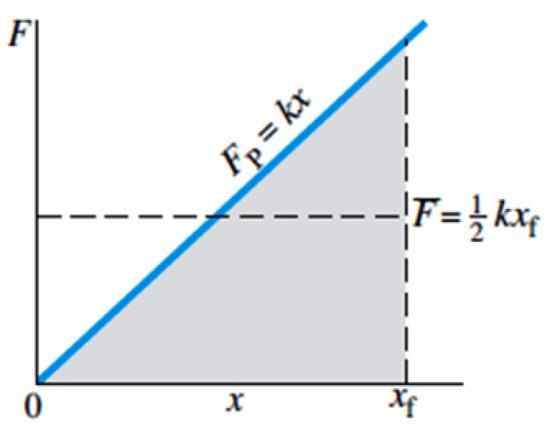Rysunek 4. Wielkość f niezbędnej siły do ​​rozciągania lub kompresji sprężyny, w zależności od deformacji x. Źródło: Giancoli, D. Fizyka z aplikacjami.

Średnia siła jest wskazana na wykresie przez F z słupkiem i jest równoważna ½ kx_F, gdzie x_F jest ostateczną pozycją wiosny.

Zarówno siła wywierana na sprężynę, jak i siła, którą wywiera na obiekt przywiązany do niego, są siłami zmiennymi. Im więcej chcesz rozciągnąć lub skompresować do sprężyny, tym więcej siły musisz zastosować, aby móc to osiągnąć.

Praca wykonana w celu rozciągania lub kompresji sprężyny

Po zastosowaniu siły, która deformuje sprężynę, wykonana jest praca przechowywana na wiosnę, która można użyć później.

Prace mechaniczne definiuje się jako obszar pod wykresem siły F w zależności od pozycji x. Aby obliczyć pracę, którą wykonuje zmienna siła f (x) podczas przenoszenia obiektu z pozycji x₁ do pozycji x₂ Należy obliczyć zdefiniowaną całkę:

W przypadku pracy niezbędnej do przyniesienia sprężyny z jej pozycji równowagi do pozycji x_F Jest to bardzo proste, ponieważ obszar, który należy obliczyć, jest obszarem szarego zacienionego trójkąta z ryc. 4, którego wzór jest znany:

Obszar trójkąta = ½ podstawa. wysokość

Dlatego niezbędna praca to:

W = ½ x_F . (KX_F) = ½ k (x_F)²

A jeśli chcesz obliczyć niezbędną pracę, aby przenieść sprężynę z pozycji x do pozycji x_F, Byłoby to równoważne obliczanie obszaru porysowanego trapezu na rycinie 5:

W = ½ k (x_F)² - ½ k x²

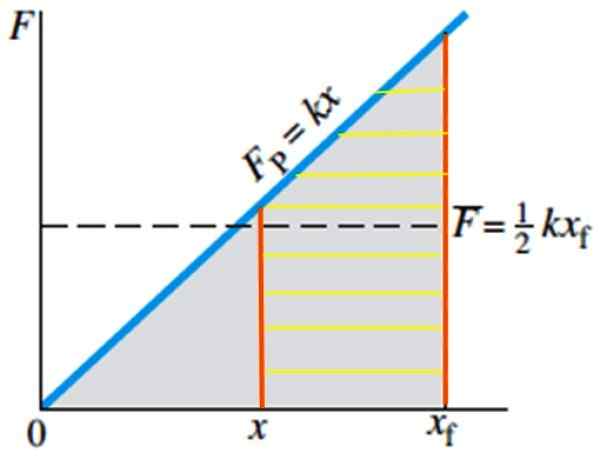Rysunek 5. Praca wykonana w celu rozciągnięcia sprężyny od pozycji x do pozycji XF równoważnej obszaru Rayada. Źródło: Giancoli, D. Fizyka z aplikacjami.

Przykłady sprężyn

Zgodnie z zastosowaniem, do którego są zamierzone, sprężyny mogą być cylindryczne, stożkowe, spiralne, z okrągłym przekrojem (najczęstszym), kwadratowego lub prostokątnego przekroju.

Może ci służyć: przewody elektryczne

Powszechnie stosowana klasyfikacja jest zgodnie z rodzajem wysiłku, do którego zostaną poddane: są skręcone, zgięcie, kompresja i rozszerzenie. Te ostatnie są szeroko stosowane i działają również na napięcie i kompresję.

Sprężyna naciskowa

Przykładem sprężyny kompresyjnej jest to, co jest używane w zabawce nazywanej Pogo albo Saltoín Palo. Sprężyny te przechowują dość potencjalną energię po ściskaniu i zwolnieniu stopniowo podczas powrotu do pozycji równowagi. W ten sposób zbiórki nie są zbyt gwałtowne.

Rysunek 6. Pogo lub Saltoín Stick opiera się na sprężynie kompresyjnej. Źródło: Wikimedia Commons.

Sprężyny rozszerzenia i skrętne

Sprężyna dla krążków jest typem sprężyn przedłużających i są wytwarzane z obrotami od studni, z dwoma haczykami na końcach. Są w stanie zachować wystarczającą energię potencjalną, którą później wypuszczają, gdy ktoś wznosi się i zaczyna wskakiwać na płótnie, które ma również własną elastyczną reakcję, jak wszystkie materiały.

Sprężyny skrętne są bardzo powszechne, ponieważ służą do tworzenia zacisków ubrania. Zamiast haczyków na końcach, zginają się pod kątem, aby oprzeć się siłom, które mają tendencję do ćwiczeń skręconych.

Rysunek 7. Sprężyny są częścią niezliczonych mechanizmów, takich jak te pincety odzieżowe. Źródło: pxfuel.

Materiały do ​​produkcji

Najbardziej odpowiednie materiały do ​​produkcji sprężyn są te z Ostateczny opór (ostateczny opór), to znaczy popierają wielki wysiłek przed złamaniem. Wygodne jest również, aby materiał miał wysoki punkt pełzania, dzięki czemu nie tracił swoich elastycznych cech z niewielkimi wysiłkami.

Sprężyny użytku przemysłowego są wytwarzane ze stopami, które obejmują stal o wysokiej zawartości węgla, miedzi, niklu i brązu.

Wnioski o prawo Hooke

Ponieważ sprężyny mają cnotę przechowywania energii potencjalnej podczas rozciągania lub kompresji, są w stanie wykonywać pracę, przesuwając takie rzeczy jak mechanizmy.

W ten sposób sprężyny mają wiele zastosowań, od małych i codziennych obiektów, przez samochody, po wszelkiego rodzaju maszyny. Sprężyny służą:

-Szokowe wibracje.

-Wyprodukujące wymobione mechanizmy: długopis, wiszące pincety, haczyki do włosów.

-Utwórz sprężynę lub dynamometry

I są również częścią mechanizmu:

Może ci służyć: zamknięty obwód elektryczny

-Zegarki.

-Trampoliny.

-Zamki.

-Zabawki.

-Bronie.

-Mierniki igły, na przykład galwanometr, używany do pomiaru prądów, napięć i rezystancji.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Nakładana jest siła wielkości 5.0 n na sprężynie, wykonując długość 3 odcinków.5 cm od jego naturalnej długości.

a) Ile jest rozciągane, gdy siła przyłożona wynosi 7 n?

b) Znajdź pracę wykonaną przez przyłożoną siłę, aby rozciągnąć się do sprężyny 3.5 cm od jego naturalnej długości.

Rozwiązanie

Wiedząc, że sprężyna jest rozciągnięta 3.5 cm poprzez zastosowanie 5.0 n możemy obliczyć twoją stałą:

k = f / x = 5.0 N / 3.5 cm = 1.43 n / cm.

Po zastosowaniu siły 7 N, uzyskano następujący odcinek:

x = f / k = 7.0 N / 1.43 n/m = 4.9 cm

Rozwiązanie b

Niezbędne prace deformowane sprężyny jest podane przez:

W = ½ kx² = 0.5 x 1.43 n / cm x (3.5 cm)² = 8.76 n . CM = 8.76 n . 1 x10 ^-2 M = 0.0876 J.

- Ćwiczenie 2

Sprężyna nikczemnego ciasta i 10 cm długości wisi na wsparciu. Jeśli powieszona jest masa 2 kg, sprężyna jest rozciągana, aż osiągnie 15 cm. Oblicz:

a) stała sprężyna

b) rozmiar sprężyny, gdy masa 3 kg jest zawieszona.

Rozwiązanie

Odcinek sprężyny to x = 15 - 10 cm = 5 cm

Ponieważ układ jest w równowadze statycznej, siła wywierana przez sprężynę podczas rozciągania jest skierowana pionowo w górę, aby zrekompensować ciężar, który jest skierowany, a następnie:

F_R = W → kx = mg

K = 2 x 9.8 N / 5 x10 ^-2 M = 392 N/m

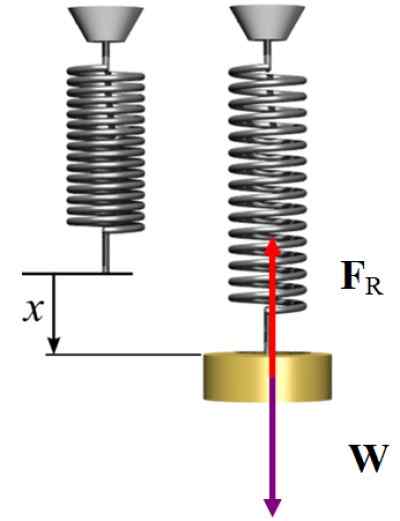Schemat wolnego ciała dla ćwiczeń rozwiązanych 2. Źródło: Wikimedia Commons/F. Zapata.

Rozwiązanie b

Gdy waga 3 kg jest zawieszona, nowa siła wynosi w = 3 x 9.8 n = 29.4 n

W tym przypadku odcinek to:

x = mg /k = 29. 4 N / 392 N / M = 0.075 M = 7.5 cm

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. BLOG MECHANIZMÓW KREATYWNYCH. Cztery różne rodzaje sprężyn. Odzyskane: CreativeMechanizmy.com.
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Głośność 2. Dynamiczny. Pod redakcją Douglas Figueroa (USB).
4. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Wyd. Prentice Hall.
5. Knight, r.  2017. Fizyka dla naukowców i inżynierii: podejście strategiczne.  osoba.