Formuła prawa biot-savart, demonstracja, aplikacje, ćwiczenia

Prawo biot-savart ustanawia związek między polem magnetycznym dB  w punkcie P, wytwarzane przez cienki drut, który przenosi prąd I i którego różnicowa długość wynosi DS. To prawo służy do znalezienia pola magnetycznego prądu rozkładów przez Zasada superpozycji. 

Oznacza to, że aby obliczyć całkowite pole magnetyczne w punkcie P, musimy dodać wszystkie wkłady, że każda część różnicowa dS drutu przyczynia się. I suma ta odbywa się poprzez całkę przeprowadzoną przez cały bieżący rozkład.

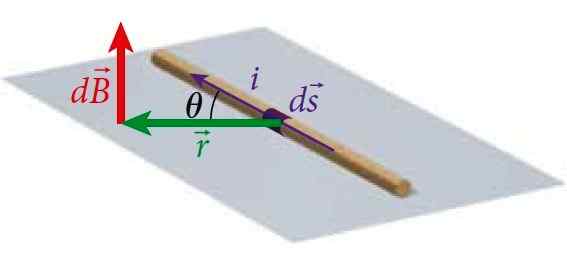
Rysunek 1. Segment drutu transportuje prąd I, który wytwarza pole magnetyczne w punkcie P w określonej odległości od drutu, które jest obliczane przez prawo biot-savart. Źródło: Bauer, w. Fizyka inżynierii i nauki.

W ten sposób możesz obliczyć pole wytwarzające przewody o prądu różnych geometrii.

Prawo Biot-Savart pochodzi od dwóch francuskich fizyków, którzy odkryli to w 1820 roku: Jean Marie Biot (1774-1862) i Felix Savart (1791-1841). Aby to osiągnąć, musieli zbadać intensywność i kształt pola magnetycznego wytwarzanego przez wiele rozkładów prądowych.

[TOC]

Formuła

Matematyczne wyrażenie prawa biot-savart jest następujące:

Utrzymuje analogie z odpowiednikiem obliczania pola elektrycznego: Prawo Coulomba, tylko że pole magnetyczne DB w p is prostopadły do płaszczyzny, w której znajduje się drut. Widzimy to na rycinie 1.

Poprzednie wyrażenie można również zapisać w następujący sposób:

W obu wyrażeniach, R Jest to wektor położenia, skierowany z elementu prądu idS do punktu, w którym chcesz obliczyć pole.

Może ci służyć: ochrona pędu liniowego: zasada, przykłady, ćwiczenia.

Ze swojej strony, R Z akcentem okrężnym jest to jednolity wektor skierowany w tym samym kierunku i kierunku, ale z modułem równym 1. Wektor R Jest reprezentowany w następujący sposób:

Z tego powodu zastępując w poprzednim równaniu -to, które ma r³ W mianowniku- wyrażenie r jest natychmiast osiągane² W mianowniku.

Oprócz wyżej wymienionych wektorów, wzór zawiera stałą μ_albo, dzwonić Przepuszczalność próżni i którego wartość to:

μ_albo = 4π x10^-7 T.M/ a.

Jeśli chcemy obliczyć wektor pola magnetycznego, konieczne jest zintegrowanie całego bieżącego rozkładu, dla którego potrzebujemy danych o jego geometrii:

Produkt wektorowy i zasada prawej strony

Prawo biot-savart obejmuje produkt wektorowy między wektorami idS I R. Wynik produktu wektorowego między dwoma wektorami jest również wektor.

W takim przypadku moduł produktu ID wektorS X R to: (ids) ⋅r⋅senθ, gdzie θ jest kątem między idS I R, Jak pokazano na rycinie 1.

W ten sposób wielkość pola dB Jest podany przez:

Kierunek i znaczenie można określić zasadą prawej ręki, co jest zilustrowane na tym rysunku:

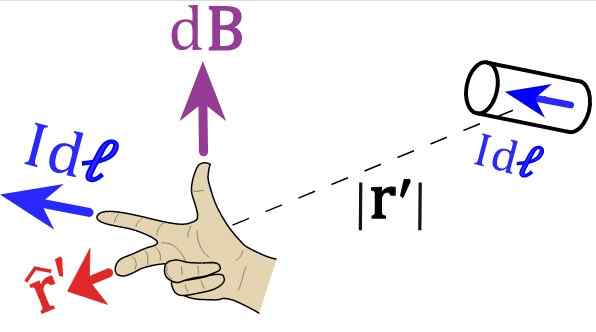Rysunek 2. Zasada prawa do prawa biot-savart. Źródło: Wikimedia Commons.

Zapraszamy czytelnika do ustawienia prawej ręki podążając za wektorami z rysunków 1 i 2. Na rycinie 1 palec wskazujący musi wskazywać w lewo, po identyfikatorzeS lub idL, Środkowy palec według wektora R jednolity.

I wreszcie kciuk jest skierowany i jest to kierunek pola magnetycznego.

Może ci służyć: elipsoid: Charakterystyka i przykłady

Demonstracja prawa biot-savart

Prawo biot-savart jest niezwykle eksperymentalne, co oznacza, że ​​jego sformułowanie wynika z wielu obserwacji dotyczących zachowania pola magnetycznego wytwarzanego przez prądowe przewody.

Obserwacje Biot i Savarta

Były to obserwacje francuskich naukowców dotyczących pola magnetycznego dB:

-Wielkość DB jest odwrotnie proporcjonalny do R².

-Jest również bezpośrednio proporcjonalny do wielkości bieżącego elementu, który nazywa się IDS A także do sen θ, gdzie θ jest kątem między wektorami dS I R.

-DB jest prostopadle do obu identyfikatorówS -kierunek prądu R.

-Różnorodne dB jest styczne do koła radiowego R skoncentrowany na drucie. Innymi słowy, pole B wytwarzane przez bieżący segment składa się z koncentrycznych obwodów dla jałowych.

-Znaczenie, w którym się kręci B Jest podany przez prawą zasadę kciuka: prawy kciuk jest skierowany w kierunku prądu, a pozostałe cztery palce są zwinięte wokół drutu, po krążeniu pola.

Wszystkie te obserwacje są łączone w matematycznym wyrażeniu wcześniej opisanego prawa.

Aplikacje dotyczące prawa biot-savart

Gdy bieżący rozkład ma wysoką symetrię, całka można łatwo rozwiązać, zobaczmy kilka przypadków:

Prostoliniowy i cienki drut

Prostoliniowy drut o długości l transportuje prąd i, taki jak ten, który pojawia się na rysunku.

Ilustruje niezbędną geometrię do obliczenia pola. Jest to prostopadłe do arkusza papieru, wychodzące do płaszczyzny, jeśli prąd przepływa od lewej do prawej, a inaczej przychodzą (sprawdź to prawą ręką).

Może ci służyć: paramagnetyzm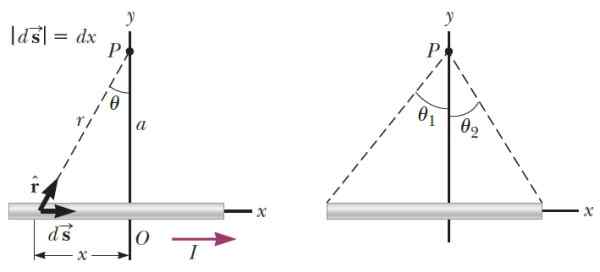Rysunek 3.- Po lewej stronie geometria niezbędna do obliczenia pola magnetycznego, które wytwarza cienki segment drutu w punkcie P. Po prawej stronie kąty, które określają pozycję p w odniesieniu do końców segmentu. Źródło: Serway, r. Fizyka nauk i inżynierii.

Być k  Wektor jednostki w kierunku prostopadłym do płaszczyzny, po przeprowadzeniu procesu integracji, pole magnetyczne, które drut wytwarza w P, wynosi:

Okrągła spira

Pętla okrągła radiowa Do Transportuje prąd, jak pokazano na rysunku i wytwarza pole magnetyczne dB -w ciemnozielonych- w punkcie P na osi osiowej, w odległości X z centrum.

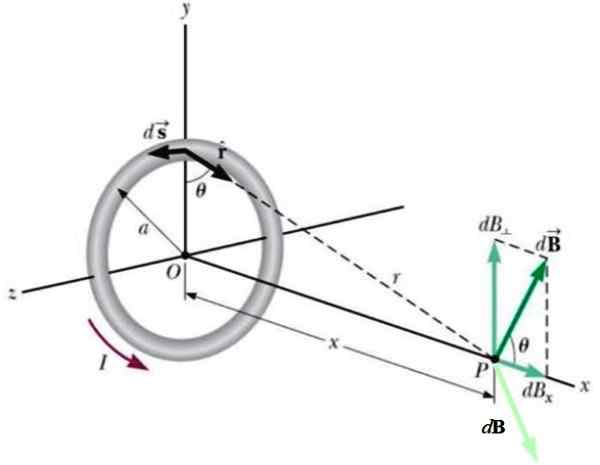Rysunek 4.- Geometria do obliczenia pola wytwarzanego przez okrągłe spaz w punkcie P na osi osiowej. Źródło: Wikimedia Commons.

Kolejny obecny element znajdujący się po przeciwnej stronie spowodowałby kolejny wkład w DB (jasnozielony), tak że jego pionowy komponent jest anulowany za pomocą pierwszego.

W rezultacie netto pole magnetyczne jest poziome, więc jest zintegrowane tylko z tymi komponentami, co skutkuje:

Ćwiczenie rozwiązane

Istnieje wyjątkowo długi drut, który przenosi prąd 2 do przepływu, jak pokazano na obrazie. Oblicz wielkość pola magnetycznego w odległości promieniowej 5 cm od drutu.

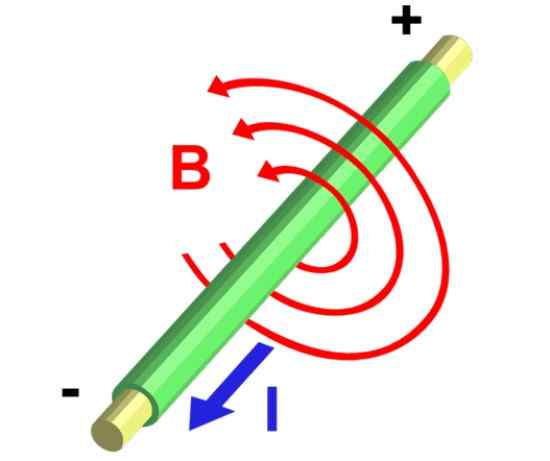Rysunek 5.- Linie pola magnetycznego w segmencie drutu prostoliniowego, który transportuje prąd. Źródło: Wikimedia Commons.

Rozwiązanie

Ponieważ jest to bardzo długi drut, możemy wziąć wyrażenie dla segmentu prostoliniowego i zrobić θ₁= 0º i θ₂ = 180º dla kątów granicznych. To wystarczy, aby długość drutu do przechowywania nieskończoności.

W ten sposób będziemy mieć pole, to:

To upraszcza:

Teraz zastępujemy wartości instrukcji:

I = 2 a

R = 5 x10^-2 M

μ_albo= 4π x10^-7 T.M/ a

Kierunek i poczucie B Pokazano je na rycinie 5, gdzie kierunek, który pozostawia arkusz, został przyjęty jako k.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 6. Elektromagnetyzm. Pod redakcją Douglas Figueroa (USB).
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Resnick, r. 1999. Fizyczny. Tom. 1. Wydanie trzecie. po hiszpańsku. Continental Editorial Company S.DO. c.V.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
6. Serway, r., Jewett, J. 2008. Fizyka nauk i inżynierii. Głośność 2. 7th. Wyd. Cengage Learning.