Odwrotne funkcje trygonometryczne, pochodzące, przykłady, ćwiczenia

Odwrotne funkcje trygonometryczne, Jak sama nazwa wskazuje, są to odpowiednie funkcje odwrotne zatoki, cosinus, styczna, cotangent, suszenie i kombajn.

Odwrotne funkcje trygonometryczne są oznaczone tą samą nazwą odpowiadającej jej bezpośredniej funkcji trygonometrycznej plus prefiks ŁUK. Zatem:

1.- Arcsen (x) Jest to odwrotna funkcja trygonometryczna funkcji Sin (x)

2.- Arccos (x) Jest to odwrotna funkcja trygonometryczna funkcji cos (x)

3.- Arctan (x) Jest to odwrotna funkcja trygonometryczna funkcji Tan (x)

4.- Arccot ​​(x) Jest to odwrotna funkcja trygonometryczna funkcji łóżeczko (x)

5.- Arcsec (x) Jest to odwrotna funkcja trygonometryczna funkcji Sec (x)

6.- Arccsc (x) Jest to odwrotna funkcja trygonometryczna funkcji CSC (x)

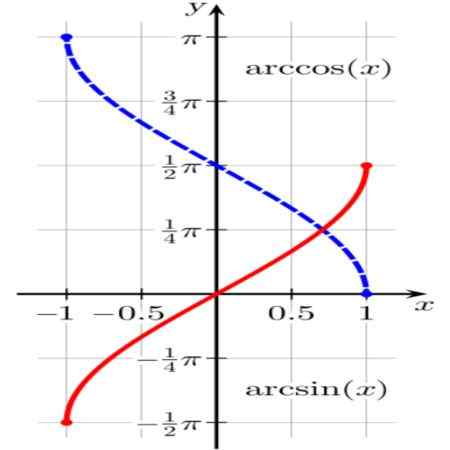
Rysunek 1. Funkcje łukowe (x) (w kolorze czerwonym) i arccos (x) (w kolorze niebieskim). Źródło: Wikimedia Commons.

Funkcja θ = arcsen (x) Powoduje to łuk jednostki θ (lub kąt w radiach θ) tak sin (θ) = x.

Zatem na przykład Arcsen (√3/2) = π/3 Ponieważ jak jest znane, piersi π/3 radian jest równy √3/2.

[TOC]

Główna wartość odwrotnych funkcji trygonometrycznych

Tak że funkcja matematyczna f (x) ma odwrotność g (x) = f^-1(x) Konieczne jest, aby ta funkcja była Invicitive, Co oznacza, że ​​każda wartość i zestaw przyjazdu funkcji f (x) pochodzi z jednej i tylko wartości x.

Jasne jest, że ten wymóg nie jest spełniony przez żadną funkcję trygonometryczną. Aby wyjaśnić punkt, zauważmy, że wartość y = 0,5 można uzyskać z funkcji zatok na następujące sposoby:

• sin (π/6) = 0,5
• Sin (5π/6) = 0,5
• sin (7π/6) = 0,5

I wiele innych, ponieważ funkcja zatok jest okresowa z okresem 2π.

Może ci służyć: wielokrotności 8: co to jest i wyjaśnienie

Aby zdefiniować odwrotne funkcje trygonometryczne, konieczne jest ograniczenie domeny ich odpowiednich bezpośrednich funkcji trygonometrycznych, aby spełniały wymóg wstrzykiwania.

Ta ograniczona domena funkcji bezpośredniej będzie głównym zakresem lub gałęzią odpowiedniej funkcji odwrotnej.

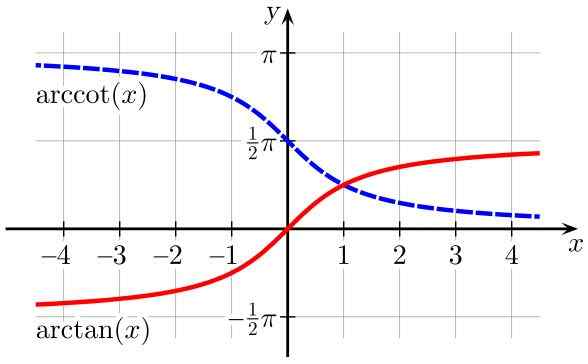Rysunek 2. ARCTAN Funkcje (x) (na czerwono) i Arccot ​​(x) (w kolorze niebieskim). Źródło: Wikimedia Commons.

Tabela domen i zakresów odwrotnych funkcji trygonometrycznych

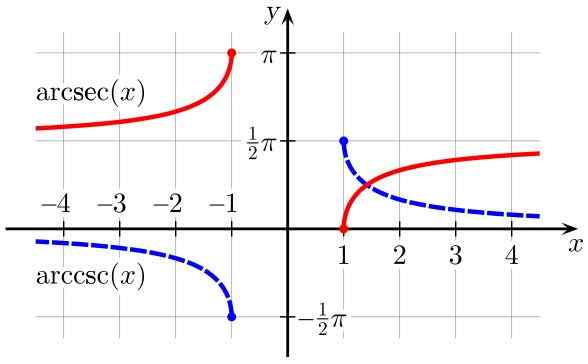Rysunek 3. Arcsec (x) (w kolorze czerwonym) i arccsc (x) (w kolorze niebieskim) (w kolorze niebieskim). Źródło: Wikimedia Commons.

Pochodzące z odwrotnych funkcji trygonometrycznych

Aby uzyskać pochodne odwrotnych funkcji trygonometrycznych, stosowane są właściwości pochodnych, w szczególności te pochodzące z funkcji odwrotnej.

Jeśli oznacza F (y) do funkcji i przez F^-1(x) Do jego odwrotnej funkcji, wówczas pochodzący z funkcji odwrotnej jest związany z pochodną funkcji bezpośredniej poprzez następującą relację:

[F^-1(x)] '= 1/ f' [f^-1(X)]

Na przykład: jeśli x = f (y) = √y jest funkcją bezpośrednią, jej odwrotność będzie

y = f^-1(x) = x². Zastosujmy zasadę pochodnej odwrotnej do tego prostego przypadku, aby zobaczyć, że ta zasada jest spełniona:

[X²] '= 1 / [√y]' = 1 / (½ i^-½ = 2 i^½ = 2 (x²)^½ = 2x 

Cóż, możemy ocenić tę sztuczkę, aby znaleźć te pochodzące z odwrotnych funkcji trygonometrycznych.

Na przykład bierzemy θ = arcsen (x) Jako funkcja bezpośrednia, jego funkcja odwrotna będzie sin (θ) = x.

[arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) =…

… = 1 / √ (1 - x²) .

W ten sposób można uzyskać wszystkie wynikające z odwrotnych funkcji trygonometrycznych, które pokazano poniżej:

Rysunek 4. Tabela osób pochodzących z odwrotnych funkcji trygonometrycznych. Źródło: Wikimedia Commons.

Te pochodne są ważne dla każdego argumentu Z należącego do liczb złożonych i dlatego są również ważne dla każdego rzeczywistego argumentu x, ponieważ Z = x + 0i.

Może ci służyć: czworobok: elementy, właściwości, klasyfikacja, przykłady

Przykłady

- Przykład 1

Znajdź Arctan (1).

Rozwiązanie

Arctan (1) jest łukiem jednostkowym (kąt w radiach) ፀ tak, że tan (ፀ) = 1. Ten kąt wynosi ፀ = π/4, ponieważ SO (π/4) = 1. Następnie Arctan (1) = π/4.

- Przykład 2

Oblicz łuk (cos (π/3)).

Rozwiązanie

Radiany kątowe π/3 są godnym uwagi kątem, którego cosinus jest ½, tak że problem jest zmniejszony do znalezienia łuku (½).

Chodzi więc o znalezienie kąt, którego sinus daje ½. Ten kąt wynosi π/6, ponieważ Sen (π/6) = Sen (30º) = ½. Dlatego Arcsen (cos (π/3)) = π/6. 

Ćwiczenia

- Ćwiczenie 1

Znajdź wynik następującego wyrażenia:

SEC (Arcan (3)) + CSC (Arccot ​​(4))

Rozwiązanie

Zaczynamy nazywać α = arcan (3) i β = arcot (4). Więc wyrażenie, które musimy obliczyć, jest takie:

SEC (α) + CSC (β)

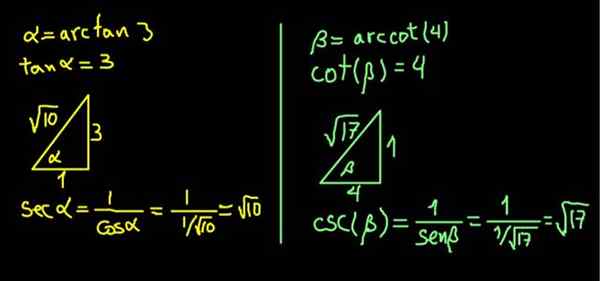
Ekspresja α = arcan (3) jest równoważna powiedzeniu tak (α) = 3.

Ponieważ styczna jest przeciwną nogą na sąsiednim, prostokątny trójkąt Cateto przeciwny α 3 jednostkami i sąsiednia kategoria 1 jednostki, tak że (α) = 3/1 = 3.

W trójkącie prostokąta hipotenusa jest określana przez twierdzenie Pitagorasa. Z tymi wartościami wynosi √10, więc:

Sec (α) = hipotenusa / sąsiadujący Cateto = √10 / 1 = √10.

Podobnie β = Arcot (4) jest równoważne, że COT (β) = 4.

Zbudowany jest trójkąt prostokąta Cateto przylegającego do β 4 jednostek i przeciwległe Cateto 1 jednostki, tak że łóżeczko (β) = 4/1.

Trójkąt jest natychmiast zakończony, znajdując hipotencję dzięki twierdzeniu Pitagorasa. W tym przypadku okazało się, że ma √17 jednostek. Następnie obliczane jest CSC (β) = hipotenusa / przeciwna cateto = √17 / 1 = √17.

Może ci służyć: y = 3sen (4x) Okres funkcji

Pamiętając, że wyrażenie, które musimy obliczyć, to: 

SEC (Arcan (3)) + CSC (Arcot (4)) = Sec (α) + CSC (β) =…

… = √10 + √17 = 3,16 + 4,12 = 7,28.

- Ćwiczenie 2

Znajdź rozwiązania:

Cos (2x) = 1 - Sen (x)

Rozwiązanie

Konieczne jest, aby wszystkie funkcje trygonometryczne były wyrażone w tym samym argumencie lub kącie. Użyjemy tożsamości podwójnego kąta:

Cos (2x) = 1 - 2 sen²(X)

Wówczas oryginalne wyrażenie jest redukowane do:

1 - 2 Sen²(x) = 1 - sin x

Po uproszczeniu i faktoryzowaniu wyraża się to jako:

sin (x) (2 Sen (x) - 1) = 0

Co daje dwa możliwe równania: sin (x) = 0 z rozwiązaniem x = 0 i inne równanie Sen (x) = ½ z x = π/6 jako rozwiązanie.

Rozwiązania podniesionego równania to: x = 0 lub x = π/6.

- Ćwiczenie 3

Znajdź rozwiązania następującego równania trygonometrycznego:

cos (x) = sin²(X)

Rozwiązanie

Aby rozwiązać to równanie, wygodne jest umieszczenie jednego rodzaju funkcji trygonometrycznej, więc użyjemy podstawowej tożsamości trygonometrycznej, aby oryginalne równanie zostało przepisane w następujący sposób:

cos (x) = 1 - cos²(X)

Jeśli nazwiemy y = cos (x), wyrażenie można przepisać jako:

I² + i - 1 = 0

Jest to równanie drugiego stopnia w i, którego rozwiązania są:

y = (-1 ± √5) / 2

Następnie wartości x spełniające oryginalne równanie to:

x = arcos ((-1 ± √5) / 2)

Prawdziwym rozwiązaniem jest znak dodatni x = 0,9046 rad = 51,83º.

Drugie rozwiązanie jest złożone: x = (π - 1,06 i) rad.

Bibliografia

1. Hazewinkel, m. 1994. Encyklopedia matematyki. Kluwer Academic Publishers / Springer Science & Business Media. 
2. Mobile Mate. Odwrotne funkcje trygonometryczne. Odzyskany z: Matemovil.com
3. Formuły wszechświata. Odwrotne funkcje trygonometryczne. Odzyskane z: Universoformulas.com
4. Weisstein, Eric W. Wynaleź funkcje trygonometryczne. Odzyskane z: Mathworld.Wolfram.com
5. Wikipedia. Wynaleź funkcje trygonometryczne. Źródło: w:.Wikipedia.com