Losowy wzór błędu i równania, obliczenia, przykłady, ćwiczenia

On błąd losowy kwoty fizycznej składa się z nieokredytowalnych wariantów miary tej kwoty. Odmiany te mogą być wytwarzane przez zjawisko mierzone przez instrument pomiarowy lub sam obserwator.

Taki błąd nie wynikał z faktu, że coś zostało zrobione źle podczas eksperymentu, ale jest to błąd związany z procesem pomiaru lub badanym zjawiskiem. Powoduje to, że miara mierzona czasem nieco większa, a czasem nieco niższa, ale zwykle oscyluje wokół wartości centralnej.

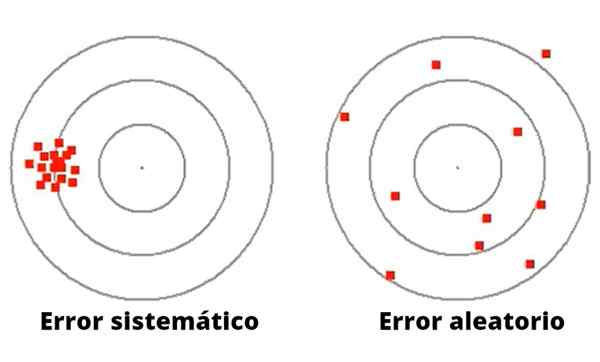
Rysunek 1- Błędy losowe różnią się wielkością i kierunkiem. Przeciwnie, systematyczne błędy są zwykle spójne.

W przeciwieństwie do błędu losowego, błąd systematyczny może być spowodowany złą kalibracją lub niewłaściwym współczynnikiem skali w instrumencie pomiarowym, w tym awarie w sprzęcie eksperymentalnym lub niewłaściwej obserwacji, która powoduje odchylenie w tym samym sensie.

Rysunek 1 ilustruje różnicę między błędem systematycznym i losowym w grze startowej DART do celu z kręgami.

W przypadku lewej strzałki są skoncentrowane wokół bardzo daleko od centrum. Pitcher tych rzutek, choć dobry cel, ma systematyczną awarię, być może pochodzenia wizualnego lub na drodze do rzucania.

Z drugiej strony miotacz po prawej (na rycinie 1) ma doskonałą dyspersję wokół centralnego celu, dlatego jest to bardzo nieprecyzyjny miotacz, ze złym celem, który mimowolnie popełnia losowy błąd.

[TOC]

Wzory i równania w losowym błędzie

Gdy proces pomiaru pokazuje błąd losowy, konieczne jest.

Oczywiście w każdym pomiarze konieczne jest dbanie o to, aby warunki, w których są przeprowadzane, są zawsze takie same.

Może ci służyć: Faraday Law: Formuła, jednostki, eksperymenty, ćwiczenia,

Załóżmy, że pomiar jest powtarzany N czasy. Ponieważ w każdym pomiarze występuje błąd losowy, będzie nieco inna wartość. Załóżmy, że zestaw N Pomiary to:

X₁, X₂, X₃,…, X_N

Więc jaka wartość zgłasza się do pomiaru? 

Średnia wartość i odchylenie standardowe

wartość środkowa albo przeciętny zbioru miar, które oznaczamy i jest obliczane w następujący sposób:

= (x₁ + X₂ + X₃ +… +X_N) / N

Odchylenie standardowe

Jednak wynik ten ma margines błędu podanego przez odchylenie standardowe. Aby to zdefiniować, musisz najpierw poznać odchylenie, a następnie wariancję:

-Odchylenie D_Siema  że każda zmierzona wartość ma Xi Jeśli chodzi o średnią wartość to:

D_Siema = x_Siema -

Gdyby obliczono średnią odchyleń, byłaby systematycznie uzyskiwana = 0, jeśli się uwzględni: 

= (d₁ + D₂ + D₃ +… +D_N) /n =

= [x₁ - ) + (x₂ - ) +… +(X_N - )]/N

= (x₁+ X₂ +… + X_N) / n - n / n = - = 0

-Średnia odchyleń nie jest przydatna, aby znać rozproszenie środków. Z drugiej strony średnia wartość kwadratu odchyleń lub wariancji, oznaczona przez σ², Tak to jest.

Oblicza się go zgodnie z następującym wzorem:

σ² = (d₁² + D₂² +.. .+ D_N² ) / (N -1)

W statystykach ta kwota jest nazywana zmienność.  

A na pierwicie kwadratowym wariancji jest znane jako Odchylenie standardowe σ:

σ = √ [(d₁² + D₂² +.. .+ D_N² ) / (n -1)] 

Odchylenie standardowe σ wskazuje, że:

1.- 68% wykonanych pomiarów jest uwzględnionych w przedziale [ - σ, + σ]. 

2.- 95% pomiarów jest w przedziale [ - 2σ, + 2σ].

3.- 99,7% podjętych środków jest w zakresie [ - 3σ, + 3σ].

Jak obliczyć błąd losowy?

Wynik pomiaru jest wartość środkowa z N Pomiary oznaczone i obliczone zgodnie z następującym wzorem:

Może ci służyć: prędkość areolowa: jak jest obliczane i rozwiązane ćwiczenia

= (∑x_Siema) / N

Jednak nie jest to „dokładna” wartość pomiaru, ponieważ na na nim wpływa Błąd losowy ε, który jest obliczany w ten sposób:

ε = σ / √n

Gdzie:

σ = √ [(∑ (xi -)² ) / (n -1)]

Ostateczny wynik pomiaru należy zgłosić na dowolny z następujących sposobów:

1. ± σ / √n = ± ε Z 68% poziomem ufności.
2. ± 2σ / √n = ± 2ε Z 95% poziomem ufności.
3. ± 3σ / √n = ± 3ε Z 99,7% poziomem ufności.

Błąd losowy wpływa na ostatnią znaczącą liczbę pomiaru, co zwykle pokrywa się z uznaniem instrumentu pomiarowego. Jeśli jednak błąd losowy jest bardzo duży, na dwie ostatnie znaczące cyfry mogą mieć wpływ zmienność.

Przykłady błędów losowych

Losowe błędy mogą pojawiać się w różnych przypadkach, w których popełniono miarę:

Mierzenie długości za pomocą taśmowej pomiaru lub reguły

Gdy długość jest mierzona regułą lub miary taśmy, a odczyty spada między markami skali, wówczas szacuje się, że wartość pośrednia.

Czasami oszacowanie ma nadmiar i inną wadę, więc do procesu pomiaru wprowadza się błąd losowy.

Rysunek 2. Losowe błędy mogą pojawiać się, gdy długość jest mierzona za pomocą taśmy taśmy. Źródło: Pikrepo.

Prędkość wiatru

W pomiarze prędkości wiatru mogą nastąpić zmiany w czytaniu z jednego momentu, ze względu na zmieniającą się naturę tego zjawiska.

Podczas czytania objętości w dyplomowym cylindrze

Gdy objętość jest odczytywana za pomocą cylindra stopniowego, nawet próba zminimalizowania błędu podobieństwa, za każdym razem, gdy jest mierzony, kąt obserwacji łąkotki zmienia się nieco, dlatego na pomiary wpływa błąd losowy.

Może ci służyć: Pierwszy warunek równowagi: wyjaśnienie, przykłady, ćwiczenia Rysunek 3.- W laboratorium chemii można popełnić losowe błędy w czytaniu cylindra absolwenta. Źródło: Pexels.

Kiedy mierzona jest postawa dziecka

Mierząc wysokość dziecka, zwłaszcza jeśli jest nieco niespokojna, powoduje, że niewielka zmiana postawy nieznacznie zmienia odczyt.

Podczas korzystania z skali łazienki

Kiedy chcemy zmierzyć naszą wagę za pomocą łazienki, niewielka zmiana w punkcie wsparcia, nawet zmiana pozycji może losowo wpłynąć na pomiar.

Ćwiczenie rozwiązane

Wskaźnik zabawek może toczyć się po prostym i pochylonym utworze i mierzony za pomocą stopu czasu, który zajmuje cały tor. 

Pomiar odbywa się 11 razy, z dbaniem o uwalnianie wózka z tego samego miejsca, bez podawania impuls.

Zestaw uzyskanych wyników to:

3,12s 3.09s 3.04S 3.04S 3.10S 3.08S 3.05S 3.10S 3.11S 3.06S, 3.03S

Jaki jest losowy błąd miar?

Rysunek 4. Zajmując czas zabawki, która schodzi przez nachyloną płaszczyznę. Źródło: Fanny Zapata.

Rozwiązanie

Jak można zobaczyć, uzyskane wyniki nie są unikalne i nieco się różnią.

Pierwszym z nich jest obliczenie średniej wartości czasu zejścia, uzyskiwaną 3,074545455 sekund.

Nie ma sensu utrzymywać tak wielu dziesiętnych, ponieważ każdy pomiar ma trzy znaczące liczby, a druga dziesiętna każdej miary jest niepewna, ponieważ jest on na granicy uznania stopwatch, dlatego wynik jest zaokrąglony do dwóch dziesiętnych:

= 3,08 s.

Z kalkulatorem w trybie statystycznym odchyleniem standardowym jest σ = 0,03 s A błąd standardowy to σ / √11 = 0,01 s. Ostateczny wynik jest wyrażany w następujący sposób:

Czas zejścia 

3,08 s ± 0,01S (z 68%poziomem ufności)

3,08 s ± 0,02 s (z 95%poziomem ufności)

3,08 s ± 0,03 s (o poziomie ufności 99,7%)

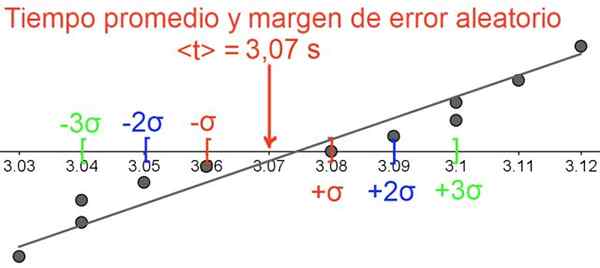Rysunek 5. Losowy margines błędu, pamiętaj, że dane są zgrupowane wokół średniej wartości. Źródło: f. Zapata.

Bibliografia

1. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
2. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
3. Helmestine a. Błąd losowy vs. Błąd systematyczny. Odzyskane z: Thoughtco.com
4. Laredo, e. Błędy środkowe. Odzyskane z: USB.Iść.
5. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.