Funkcja zatrzymująca, właściwości, przykłady

A Funkcja zatrzymująca Jest to każda relacja, w której każdy element należący do Codominium jest obrazem co najmniej jednego elementu domeny. Znany również jako funkcja o, Są częścią klasyfikacji funkcji dotyczących sposobu powiązania ich elementów.

Na przykład funkcja F: a → B określony przez F (x) = 2x

Który jest czytany "F to się wychodzi DO dopóki B określony przez F (x) = 2x "

Dotknij Zdefiniuj zestawy początkowe i przyjazdu A i b.

A: 1, 2, 3, 4, 5 Teraz wartości lub obrazy, które każdy z tych elementów zostaną wydane po ocenie F, Będą elementami Codominium.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

W ten sposób tworząc zestaw B: 2, 4, 6, 8, 10

Można zatem stwierdzić, że:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 określony przez F (x) = 2x jest funkcją zatrzymywania

Każdy element kodominium musi być co najmniej jedną operacją zmiennej niezależnej poprzez daną funkcję. Nie ma ograniczania obrazu, element Codominium może być obrazem więcej niż jednego elementu domeny i kontynuować radzenie sobie z Funkcja zatrzymująca.

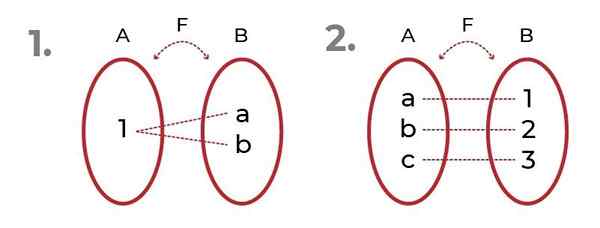
Obraz pokazuje 2 przykłady z Funkcje onjective.

Źródło: Autor

W pierwszym obserwuje się, że obrazy można odnieść do tego samego elementu, bez uszczerbku Otrukowanie funkcji.

W chwili widzimy sprawiedliwy rozkład między domeną a obrazami. To powoduje Funkcja biejcive, gdzie kryteria Funkcja iniekcyjna i funkcja zatrzymująca.

Inna metoda identyfikacji Funkcje onjective, jest sprawdzenie, czy kodominium jest równe stopnie funkcji. Oznacza to, że jeśli zestaw przylotów jest równy obrazom dostarczonym przez funkcję podczas oceny zmiennej niezależnej, Funkcja jest zatrzymująca.

[TOC]

Nieruchomości

Rozważyć Zadowocka Następujące należy spełnić funkcję:

Być F: d_F → C_F

∀ B ℮ C_F  I do ℮  D_F   / F (a) = b

To jest algebraiczny sposób na ustalenie tego Dla wszystkich „b”, który należy do c_F Istnieje „A”, który należy do D_F  tak, że funkcja F oceniona w „A” jest równa „B”. 

Może ci służyć: radykalne właściwości

Otwarcie jest osobliwością funkcji, w których kodominium i ranga są podobne. Zatem elementy ocenione w funkcji składają się na zestaw przyjazdu.

Warunkowanie funkcji

Czasami funkcja, która nie jest Zadowocka, może przejść pewne warunkowanie. Te nowe warunki mogą zamienić go w Funkcja zatrzymująca.

Wszystkie rodzaje modyfikacji domeny i kodominium funkcji są prawidłowe.

Przykłady: Rozwiązane ćwiczenia

Aby spełnić warunki Otrukowanie Należy zastosować różne techniki warunkowania, aby upewnić się, że każdy element Codominium znajduje się w zestawie obrazów funkcji.

Ćwiczenie 1

• Być funkcją F: r → R zdefiniowane przez linię F (x) = 8 - x

Odp.: [Wszystkie liczby rzeczywiste]

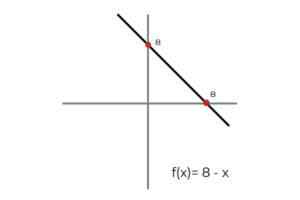Źródło: Autor

W takim przypadku funkcja opisuje ciągłą linię, która obejmuje wszystkie liczby rzeczywiste zarówno w ich dziedzinie, jak i zakresie. Ponieważ ranga funkcji R_F Jest równy Codominium R Można stwierdzić, że:

F: r → R zdefiniowane przez linię F (x) = 8 - x jest Funkcja zatrzymująca.

Dotyczy to wszystkich funkcji liniowych (funkcji, których większy stopień zmiennej to jeden).

Ćwiczenie 2

• Przestudiuj funkcję F: r → R określony przez F (x) = x² : Zdefiniuj, czy jest to Funkcja zatrzymująca. W przypadku, gdy tak nie.

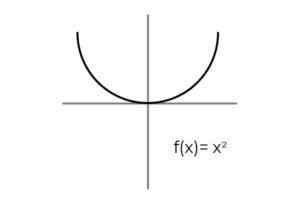Źródło: Autor

Pierwszą rzeczą do rozważenia jest Codominium F, który składa się z rzeczywistych liczb R. Nie ma sposobu, aby funkcja wyrzuciła wartość ujemną, która wyklucza negatywne rzeczywiste wśród możliwych obrazów.

Kondycjonowanie interwału Codominium [0 , ∞ ]. Unika się, aby pozostawić elementy CO -alomio bez relacji F.

Obrazy są powtarzane dla par elementów zmiennej niezależnej, takich jak x = 1 I x = - 1.  Ale to tylko wpływa Wtryskiwanie  funkcji, nie jest problemem dla tego badania.

Może ci służyć: kolejne pochodne

W ten sposób można stwierdzić, że:

F: r  →[0, ∞ ) określony przez F (x) = x²    Jest to funkcja zatwierdzająca

Ćwiczenie 3

• Zdefiniuj warunki Codominium Zadowocka do funkcji

F: r  → R określony przez F (x) = sin (x)

F: r  → R określony przez F (x) = cos (x)

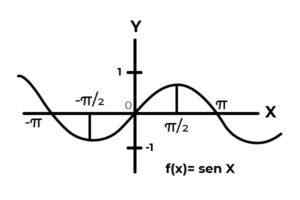Źródło: Autor 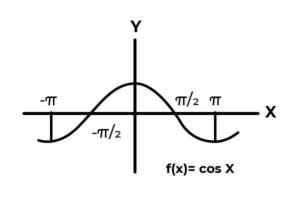Źródło: Autor.

Zachowanie funkcji trygonometrycznych jest podobne do zachowania fal, ponieważ jest bardzo powszechne w znalezieniu powtórzeń zmiennej zależnej między obrazami. Również w większości przypadków zakres funkcji jest ograniczony do jednego lub więcej sektorów prawdziwej linii.

Tak jest w przypadku funkcji sinus i cosinus. Gdzie ich wartości zmieniają się w przedziale [-1, 1]. Wspomniany interwał musi warunkować kodominium, aby osiągnąć kopertę funkcji.

F: r  →[-eleven] określony przez F (x) = sin (x)  Jest to funkcja zatwierdzająca

F: r  →[-eleven]określony przez F (x) = cos (x) Jest to funkcja zatwierdzająca

Ćwiczenie 4

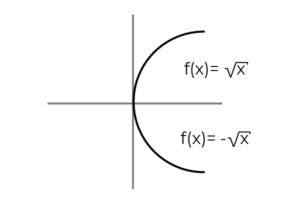
• Przestudiuj funkcję

F: [0, ∞ ) → R określony przez F (x) = ± √x   Oznacz, czy jest to Funkcja zatrzymująca

Źródło: Autor

Funkcja F (x) = ± √x  Ma specyfikę, która definiuje 2 zmienne zależne w każdej wartości „x” . Oznacza to, że zakres otrzymuje 2 elementy dla każdego z nich przeprowadzanych w domenie. Wartość dodatnią i ujemną dla każdej wartości „x” należy zweryfikować dla każdej wartości „x”.

Podczas obserwowania zespołu początkowego zauważono, że domena została już ograniczona, w celu uniknięcia nieokreślonych wytworzonych podczas oceny liczby ujemnej w korzeniu momentu obrotowego.

Podczas weryfikacji zakresu funkcji pokazuje, że każda wartość Codominium należy do zakresu.

W ten sposób można stwierdzić, że:

F: [0, ∞ ) → R określony przez F (x) = ± √x  Jest to funkcja zatwierdzająca

Może ci służyć: wektory współbieżne: cechy, przykłady i ćwiczenia

Ćwiczenie 4

• Przestudiuj funkcję F (x) = ln x  Oznacz, czy jest to Funkcja zatrzymująca. Warunek zestawów przybycia i odlotu w celu dostosowania funkcji do kryteriów przepisywności.

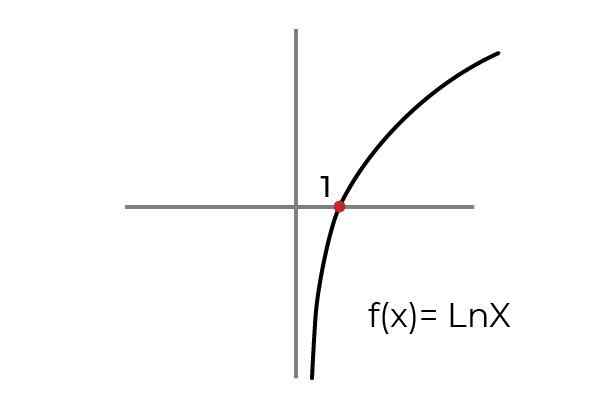Źródło: Autor

Jak pokazano na wykresie, funkcja F (x) = ln xjest zdefiniowane dla wartości „x” większych niż zero. Podczas gdy wartości „i” lub obrazów mogą przybierać jakąkolwiek rzeczywistą wartość.

W ten sposób możemy ograniczyć domenę F (x) = do przedziału (0 , ∞ )

Podczas gdy stopień funkcji może być utrzymywany jako zestaw liczb rzeczywistych R.

Biorąc to pod uwagę, można stwierdzić, że:

F: [0, ∞ ) → R określony przez F (x) = ln x  Jest to funkcja zatwierdzająca

Ćwiczenie 5

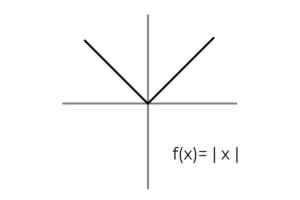
• Badaj funkcję wartości bezwzględnej F (x) = | x | i wyznaczyć zestawy przybycia i wyjazdu, które są zebrane zgodnie z kryteriami lojalności.

Źródło: Autor

Domena funkcji jest wypełniona dla wszystkich liczb rzeczywistych R. W ten sposób jedyne warunkowanie musi być przeprowadzone w Codominium, biorąc pod uwagę, że funkcja wartości bezwzględnej bierze tylko wartości dodatnie.

Codominium funkcji jest ustalone wyrównanie go do zakresu tego samego

[0 , ∞ )

Teraz można stwierdzić, że:

F: [0, ∞ ) → R określony przez F (x) = | x |  Jest to funkcja zatwierdzająca

Proponowane ćwiczenia

1. Sprawdź, czy następujące funkcje są zatrzymujące:

• F: (0, ∞ ) → R określony przez F (x) = log (x + 1)
• F: r → R określony przez F (x) = x³
• F: r →[1, ∞ )  określony przez F (x) = x²  + 1
• [0, ∞ ) → R określony przez F (x) = log (2x + 3)
• F: r → R określony przez F (x) = sec x
• F: r - 0 → R określony przez F (x) = 1 / x

Bibliografia

1. Wprowadzenie do logiki i krytycznego myślenia. Merrilee H. Łosoś. University of Pittsburgh
2. Problemy w analizie matematycznej. Piotr Bilar, Alfred Witkowski. University of Wroclaw. Polak.
3. Elementy analizy abstrakcyjnej. Mícheál O'Searcoid Phd. Departament Matematyki. University College Dublin, Beldfield, Dubllind 4
4.  Wprowadzenie do logiki i metodologii nauki dedukcyjnej. Alfred Tarski, Nowy Jork Oxford. Oxford University Press.
5.  Zasady analizy matematycznej. Enrique Linés Escardó. Redakcja Reverté s. Do 1991. Barcelona, ​​Hiszpania.