Typy frakcji, przykłady, ćwiczenia rozwiązane

 frakcje albo liczby ułamkowe Są to liczby, które są reprezentowane, wskazujące iloraz między dwoma liczbami całkowitych Do I B, dopóki B różni się od 0. Na przykład 1/3 to ułamek, który brzmi jako „jedna trzecia”.

Do liczby Do Jest znany jako licznik ułamka frakcji i B Jak mianownik Tego samego. Mianownik wskazuje, ile części należy podzielić całość. Ze swojej strony licznik wskazuje, ile części tej całości.

Rysunek 1. Ile porcji ma ten bar czekoladowy? Źródło: Piqsels.

Całość to wszystko, co chce podzielić lub ułamać, na przykład pizzę lub batonik pokazany na rycinie 1. Pasek jest wykonany w taki sposób, że bardzo łatwo jest go podzielić na 5 równych części, gdzie każda część równa się 1/5 pełnego paska.

W ułamku lub frakcyjnym numerze 1/5 licznik jest wart 1, a mianownik jest wart 5. Frakcja brzmi „Piąta”.

Załóżmy, że jemy 3 kawałki czekolady. Powiedzielibyśmy, że zjedliśmy 3/5 części baru, a 2/5 części pozostało do podzielenia się z przyjacielem. Możemy również powiedzieć, że jedliśmy „trzy piąte czekolady” i dajemy przyjacielowi „dwie piąte”.

Reprezentacja graficzna tych liczb ułamkowych jest następująca:

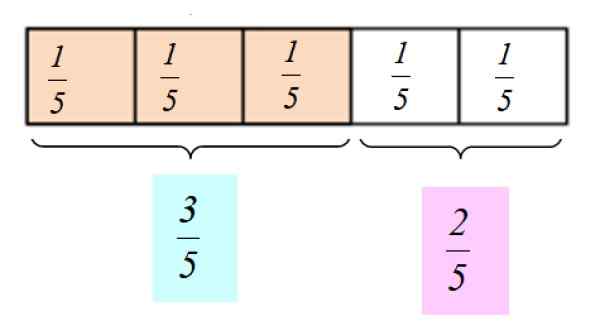Rysunek 2.- Graficzna reprezentacja frakcji 3/5 i 2/5. Źródło: f. Zapata.

[TOC]

Rodzaje ułamków

Własne frakcje

Ułamek jest jego własną, gdy licznik jest mniejszy niż mianownik, a zatem jego wartość jest mniejsza niż 1. Frakcje z poprzedniej sekcji, w przykładzie czekolady, to ich własne ułamki.

Inne przykłady ich własnych frakcji to: ½; 8/10; 3/4 i więcej.

Rysunek 3.- Zarówno 1/4, jak i 1/2 to ich własne frakcje. Źródło: Wikimedia Commons.

Niewłaściwe ułamki

Licznik niewłaściwych frakcji jest większy niż licznik. Na przykład 4/3, 8/5, 21/10 należy do tej kategorii.

Pozorne ułamki

Frakcje te reprezentują całą liczbę. Wśród nich są 4/2, 10/5 i 27/3, ponieważ jeśli dobrze będziemy wyglądać, wynik dzielenia licznika między mianownikiem tych frakcji daje liczbę całkowitą.

Zatem: 4/2 = 2, 10/5 = 2 i 27/3 = 9.

Równoważne ułamki

Dwie frakcje N/M i P/Q są równoważne podczas podziału licznika między mianownikiem, uzyskano tę samą kwotę. W ten sposób równoważne ułamki reprezentują tę samą część całości.

Jako przykład mamy ułamki: 15/2 i 30/4. Dzieląc 15 przez 2 dostajesz 7.5, ale jest to również takie samo, jeśli 30 jest podzielone przez 4.

Może ci służyć: funkcja iniekcyjna: z czego składa się, do czego jest i przykłady

Aby wiedzieć, czy dwie frakcje N/M i P/Q są równoważne, zweryfikowana jest zgodność z następującą równością:

N*q = m.P

Nieredukowalne frakcje

Gdy licznik i mianownik są podzielone zarówno przez tę samą figurę, jak i tak długo, jak wynik jest całości, uzyskuje się frakcję równoważną oryginałowi, ale z mniejszymi liczbami.

Proces ten trwa, gdy licznik i mianownik mają ten sam dokładny dzielnik. Kiedy nie jest możliwe kontynuowanie dzielenia Nieredukowalna frakcja oryginalnej frakcji.

Zaletą, która musi pracować z nieredukowalną frakcją jest to, że uzyskuje się równoważną frakcję, ale z mniejszymi liczbami. Dlatego kiedy pracujesz z ułamkami, musisz upewnić się, że je w miarę możliwości zmniejszy, aby ułatwić obliczenia.

Załóżmy, że frakcja 12/20, będąc pary liczników i mianowników, oba można podzielić przez 2:

12/20 = 6/10

I jeszcze raz:

6/10 = 3/5

Frakcja 3/5 jest równoważna 12/20, ale prostsza.

Liczby mieszane

Niewłaściwa frakcja przyznaje również reprezentację jako liczbę mieszaną, zwaną tak, ponieważ ma całą część i inną część ułamkową, a część ułamkowa jest ułamkiem własnej.

Spójrzmy na szybki przykład z ułamkiem 15/2, który, jak wiemy, jest równoważny 7.5.

Możemy wyrazić do 15/2 jako liczbę mieszaną tak:

15/2 = 7 + 0.5

Ale 0.5 = ½. Dlatego 15/2 = 7½, które czyta „siedem i medium”.

Przykłady ułamków

Liczby ułamkowe są konieczne, ponieważ zarówno naturalne, jak i liczby całkowite są niewystarczające, gdy chcemy podzielić takie rzeczy, jak pręt czekoladowy.

I dlatego istnieje nieskończona różnorodność pomiarowych wzorców i obiektów, których specyfikacje obejmują liczby ułamkowe, nie wspominając o ilości codziennych sytuacji, w których są one konieczne.

Zakupy żywności

W krajach, w których stosuje się dziesiętny system metryczny, stosowanie kilo jest powszechne w odniesieniu do wagi wielu produktów spożywczych. Nie zawsze chcemy kupować całe kwoty, ale trochę więcej lub trochę mniej.

Dlatego pytamy:

• ½ kg ryb
• ¾ kg pomidorów
• ¼ kilograma cebuli
• 1 ½ kg brzoskwini (1 i pół kilograma).

A podczas korzystania z wzorów pomiaru anglo -sakonu to samo dzieje się: potrzebujemy 2 i pół funta lub 1/4 czegoś czegoś.

Może ci służyć: ocena funkcji

Wszystkie te liczby są ułamkowe i, jak widzieliśmy, odpowiadają dwóm różnym rodzajom frakcji: własnych i niewłaściwych.

Przepisy kuchenne

Przepisy kuchenne często wykorzystują liczby ułamkowe, aby wskazać liczbę niektórych składników. Na przykład:

• ½ szklanki mąki
• ¾ kg cukru, aby przygotować ciasto.

Długości i średnice

Wymiary mebli, tkaniny i wszelkiego rodzaju przybory domowe są mierzone we frakcjach metra czy cale, niezależnie od tego, czy stosuje się układ metryczny miary, czy anglo -sakson.

Nawet w krajach, w których dominuje dziesiętny system metryczny, komercyjna miedź, stal i inne materiały hydrauliczne zwykle są o średnicach określonych w calach. Podobnie inne elementy sprzętowe, takie jak śruby i nakrętki.

Jako cal jest równoważny 2.54 cm, zwykle te elementy, które mają niewielkie średnice, są wyrażane w frakcjach calowych.

Bardzo powszechne środki dla rur domowych to:

• ½ cala
• ¼ cala
• 3/8 i 5/8 cala.

Przeloty czasowe

Codziennie liczby ułamkowe są używane do wyrażania odstępów czasu, takich jak ¼, ½ i ¾ godziny, a nawet nieco większa: 1 godzina i ¼ i tak dalej.

Rysunek 4. Są w połowie jedenaście na tym zegarku. Źródło: Pixabay.

Ćwiczenia z ułamkami

- Ćwiczenie 1

Dzisiaj Juanito zajął ciasto na swoje urodziny do szkoły i chce rozpowszechniać je między wszystkimi swoimi przyjaciółmi, ale nauczyciel chce dać utwór trzykrotnie większy w odniesieniu do dzieci.

Biorąc pod uwagę, że są 24 dzieci + nauczyciel, z którymi chce dać odpowiednik trzech kawałków, ile kawałków powinno wyciąć ciasto?

Rozwiązanie

Gdyby Juanito chciał tylko rozpowszechniać ciasto wśród swoich przyjaciół, każdy z nich odpowiadałby 1/24.

Ale ponieważ nauczyciel chce podać część i że utwór jest trzy razy większy, musiałbym rozdzielić ciasto wśród 24 uczniów + 3 sztuk dla nauczyciela. Oznacza to, że każde dziecko odpowiada 1/27 sztuk, a nauczyciel 3/27 sztuk.

Ponadto, jeśli zmniejszymy ułamek 3/27, zachęcimy nauczyciela do wzięcia 1/9 części ciasta.

- Ćwiczenie 2

Firma z szefem i trzema pracownikami ma 6000 EUR dochodów każdego miesiąca. Ile pieniędzy odpowiada każda osoba, jeśli szef chce zachować połowę tego, co wygrał?

Może ci służyć: Rhomboid: Charakterystyka, jak wyjąć obwód i obszar

Rozwiązanie

Jeśli szef chce wygrać połowę, musi zostać z 6000/2, co zarabia 3000 €. Z pozostałych 3000 € jest tym, co trzej pracownicy powinni być dystrybuowane. W ten sposób każdy pracownik wygra 3000/3, co daje 1000 €.

- Ćwiczenie 3

Znajdź nieredukowalną część:

a) 12/18 i b) 4/11

Rozwiązanie

W pierwszym przypadku zauważyliśmy, że zarówno licznik, jak i mianownik są równe i podzielne między 2. Są również podzielne między 3, ponieważ 12–18 to wielokrotności tej figury.

Więc możemy uprościć ułamek, dzieląc zarówno licznik, jak i mianownik od 2 lub 3.

Zaczynając od podzielenia przez 2:

12/18 = 6/9

Teraz zauważamy, że zarówno licznik, jak i mianownik tej równoważnej frakcji są wielokrotnościami 3, więc dzieląc oba między tym rysunkiem:

6/9 = 2/3

A ponieważ 2 i 3 są liczbami pierwszymi, nie mają już żadnego innego wspólnego dzieliny, z wyjątkiem 1. Osiągnęliśmy nieredukowalną frakcję.

Maksymalny wspólny dzielnik MCD licznika i mianownika można było również obliczyć. Dla 12 i 18:

MCD (12,18) = 6.

A następnie licznik i mianownik są podzielone przez tę liczbę, co jest równoważne robienie tego etapów.

Rozwiązanie b

Tutaj obserwujemy, że 11 jest liczbą pierwszą, a jego dzielnicy to 1 i 11. Ze swojej strony 4 przyznaje się do dzielników do 4, 2 i 1. Z wyjątkiem 1, liczby te nie mają wspólnego dzielnika, a zatem frakcja 4/11 jest nieredukowalna.

- Ćwiczenie 4

Wskaż, który jest największym ułamkiem każdej pary:

a) ¾ i 5/4

b) 3/7 i 4/9

Rozwiązanie

Kiedy dwie pozytywne ułamki mają ten sam mianownik, największy jest taki, który ma największy licznik. Dlatego 5/4 jest większe, ponieważ 5> 3.

Rozwiązanie b

Jeśli frakcje N/M i P/Q mają inny mianownik i oba są pozytywne, kryteria porównawcze są następujące:

Bez.Q> m. P, a następnie N/M> P/Q

Inną opcją jest znalezienie dziesiętnego wyrażenia każdej frakcji i porównanie.

Zgodnie z pierwszym kryterium: n = 3, m = 7, p = 4, q = 9. Dlatego: n.Q = 3*4 = 12 i i.P = 7*4 = 28.

Jak 12< 28, ocurre que 3/7 < 4/9.

Lub wyrażamy każdą frakcję jako dziesiętną, uzyskując to:

3/7 = 0.428571428… .

4/9 = 0.44444444… .

Punkty zawiesinowe wskazują, że ilość dziesiętnych jest nieskończona. Ale to wystarczy, aby to sprawdzić, że rzeczywiście 4/9> 3/7.

Bibliografia

1. Baldor, a. 1986. Arytmetyka. Codex Editions and Dystrybucje.
2. Carena, m. 2019. Podręcznik matematyki. National University of the Coast.
3. Figuera, J. 2000. Matematyka 8. Edycje CO-Bo.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Strona matematyczna. Co to jest ułamek? Odzyskany z: themathpage.com.