Frakcje równoważne 2/3

frakcje równoważne ⅔ (Czytane są dwie trzecie) są tymi, których wartość, wyrażona w sposób dziesiętny, jest tym samym, który jest uzyskiwany przez podzielenie 2 przez 3: 0.6666… punkty zawiesinowe wskazują, że 6 pojawia się nieskończone czasy w tym dywizji.

Ułamek równoważny 2/3 to ułamek 4/6, ponieważ okazuje się, że po rozwiązaniu podziału między 4 a 6 wyraźnie dziesiętne 0,6666 .. . Następnie można powiedzieć, że 4/6 = 2/3 = 0,6666 .. .

Frakcje 2/3 i 4/6 są równoważne, ponieważ dzieląc liczbę licznika przez mianownik ten sam numer gazety 0.66666 .. . (Źródło: F. Zapata)

Frakcja, jak sama nazwa wskazuje, to część lub część urządzenia. Frakcja ⅔ jest uzyskiwana przez podzielenie urządzenia na trzy równe części i biorąc dwie z tych części.

Każda frakcja składa się z górnej części, zwanej licznik ułamka, oddzielone od dołu lub mianownik, Przez linię ułamka. Mianownik wskazuje, ile części jest podzielona jednostka, a licznik wskazuje, ile z tych stron należy wziąć pod uwagę.

Teraz rozważ frakcję 4/6 (czytaj cztery szóste). Udowodniono, że ułamek ten jest równoważny ⅔, ponieważ aby podzielić jednostkę na sześć części, należy wykonać te kroki:

1. Podziel jednostkę na trzy równe części.
2. A następnie podziel każdą z tych części przez połowę, uzyskując w sumie sześć równych części.

Jeśli zgrupowane są 4 części 1/6 urządzenia, uzyskana kwota stanowi ułamek identycznej wartości, z którą uzyskuje się 2 części 1/3 urządzenia. Na poniższym wykresie przeprowadzana jest opisana procedura: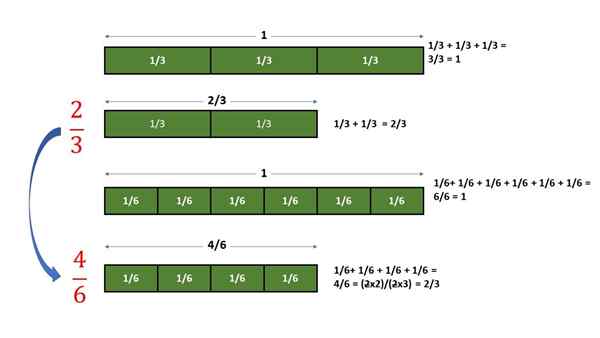

Weryfikacja graficzna, że ​​frakcja 2/3 jest równoważna frakcji 4/6. Źródło: f. Zapata.

Może ci służyć: analogie numeryczne: typy, aplikacje i ćwiczenia

Metody znalezienia równoważnych ułamków

Zauważ, że równoważna frakcja 4/6 można uzyskać z 2/3 przez pomnożenie zarówno licznika, jak i mianownika tego ostatniego.

Gdy jednocześnie mnożą licznik i mianownik frakcji według tej samej liczby, uzyskuje się równoważną frakcję.

Innym sposobem znalezienia ułamka równoważnego drugiego byłoby podział licznika i mianownika przez tę samą kwotę, pod warunkiem, że licznik i mianownik są dokładnie podzielne według tej samej liczby. Ale nie można osiągnąć, przez podział tej samej liczby całkowitej, równoważnej frakcji opartej na 2/3, ponieważ liczby 2 i 3 są ze sobą kuzynami.

Kiedy licznik i mianownik ułamka są ze sobą liczbami pierwszymi, mówi się, że ułamek jest nieskracalny. A frakcja 2/3 jest dobrym przykładem tego rodzaju frakcji, w rzeczywistości 2/3 reprezentuje zestaw wszystkich frakcji równoważnych 0.666 ..

Z drugiej strony, ułamek 4/6 jest redukowalny i równoważny frakcji ⅔, ponieważ licznik 4 i mianownik 6 są liczbami parzystymi, obie podzielne przez 2.

Tak więc dwa sposoby uzyskania ułamków równoważnych danej, to:

• Jednocześnie wzmacniają licznik i mianownik 
• Zmniejsz licznik i mianownik

Wzmocnienie ułamków

Aby uzyskać ułamek równoważny danej, licznik i mianownik są mnożone przez tę samą rysunek. Oto kilka przykładów:

Stwierdzono, że ⅔ (dwie trzecie), 4/6 (cztery szóste), 6/9 (sześć dziewiąty) i 8/12 (osiem dwunasty) są ze sobą równoważne frakcje, ale z nich tylko ⅔ jest nieredukowalne frakcja.

Podsumowując, jeśli zaczniesz od frakcji nieredukowalnej ⅔, sposobem na uzyskanie innej równoważnej frakcji jest zastosowanie tej wzoru:

Może ci służyć: rozdzielone ćwiczenia czynnikowe

Z liczbą całkowitą.

Metoda amplifikacji w celu uzyskania równoważnych frakcji. Źródło: f. Zapata

Zmniejszenie ułamków

Jest to metoda, która umożliwia uzyskanie równoważnej frakcji, pod warunkiem, że ułamek początkowa ma licznik i mianownik z jednym lub bardziej popularnymi dzielnikami.

Nie jest to przypadek 2/3, które jak powiedziano wcześniej, jest nieredukowalne. Ale na przykład ułamek 60/90 (Sześćdziesiąt dziewięćdziesiątych) Można go zmniejszyć do:

• 6/9, ponieważ zarówno licznik, jak i mianownik są podzielne między dziesięć.
• 30/45, ponieważ licznik i mianownik są podzielne między dwoma.
• 20/30, ponieważ licznik i mianownik są podzielne między trzema.
• 12/18, ponieważ licznik i mianownik są podzielne między pięć.

Jeśli chcesz uzyskać nieredukowalną frakcję równoważną oryginałowi, konieczne jest podzielenie zarówno licznika, jak i mianownika przez jego maksymalny wspólny dzielnik (MCD).

Rozkład w czynnikach ma licznik:

60 = 2² ⋅ 3 ⋅ 5

I przeprowadzanie tej samej procedury w mianowniku:

90 = 2 ⋅ 3² ⋅ 5

MCM są wspólnymi czynnikami pierwszymi z niższym wykładnikiem, to znaczy:

MCM (60; 90) = 2⋅3⋅5 = 30

Następnie 60 między 30 da 2, który jest umieszczony w liczniku i na 90 między 30 da 3, 3 jest umieszczony w mianowniku. Dlatego frakcję nieredukowalną 60/90 można wyrazić jako:

Sposoby ustalenia, czy dana frakcja jest równoważna 2/3

Bezpośrednim sposobem, aby dowiedzieć się, czy dwie lub więcej frakcji są równoważne, jest wyrażanie frakcji bezpośrednio w sposób po przechyłek, a jeśli wszystkie cyfry pokrywają się, jest pewne, że ułamki są równoważne. Ale istnieją inne metody mające na 2/3:

Metoda 1

Być ułamkiem x/y

Znak przesłuchania jest umieszczony, ponieważ nie jest jeszcze znany, czy wartości „x” i „y” spełniają równość. Wiedzieć, że to mnoży się w krzyżu:

Może ci służyć: Relacje proporcjonalne: koncepcja, przykłady i ćwiczenia

3x =? 2 i

Tylko wtedy, gdy równość jest wypełniona, istnieje pewność, że X/Y jest ułamkiem równoważnym 2/3.

Metoda 2

Ta metoda wymaga ustalenia maksymalnego wspólnego dzielnika (MCD) licznika i mianownika. Następnie oba są podzielone przez MCD, a jeśli frakcja uzyskana po przeprowadzeniu opisanej operacji wynosi 2/3, można powiedzieć, że jest to ułamek równoważny.

Przykłady

Przykład 1

Ustal, czy ułamek 40/60 jest równoważny ⅔.

Rozwiązanie

Metodą 1:

Metoda wskazuje, że należy ją pomnożyć w krzyżu:

40 x 3 =? 60 x 2

120 =? 120

Ponieważ równość jest wypełniona, stwierdza się, że 40/60 jest równoważne 2/3.

Przykład 2

Ustal, czy ułamek 120/180 jest równoważny ⅔.

Rozwiązanie

W tym przykładzie stosuje się metoda 2. Pierwszą rzeczą jest określenie rozkładu w podstawowych czynnikach 120:

120 = 2³ ⋅ 3 ⋅ 5

A rozkład w czynnikach mianownika jest:

180 = 2² ⋅ 3² ⋅ 5

Aby określić MCD, wspólne czynniki są mnożone za pomocą niższego wykładnika:

MCD (120; 180) = 2² ⋅ 3 ⋅ 5 = 60

Więc:

120 ÷ 60 = 2

180 ÷ 60 = 3

Stwierdzono więc, że 120/180 jest równoważne 2/3, to znaczy:

Rozwiązane ćwiczenia

Ćwiczenie 1

To frakcje 10/15 i 12/18 równoważne?

Rozwiązanie

Najszybszym sposobem na weryfikacji jest pomnożenie się w krzyż, ponieważ nie są to bardzo duże wartości:

10 x 18 =? 15 x 12

180 =? 180

Uzyskano równość, wówczas można powiedzieć, że 10/15 = 12/18.

Ćwiczenie 2

To frakcje 8/12 i 12/20 równoważne ⅔?

Rozwiązanie

Zostanie zastosowana metoda uproszczenia, która polega na podzieleniu jednocześnie licznika i mianownika przez wspólne czynniki pierwotne, aż do osiągnięcia nieredukowalnego wyrażenia:

12/12 = 4/6 = ⅔, to znaczy, pierwsza frakcja jest równoważna ⅔.

Za drugą ułamek:

12/20 = 6/10 = ⅗, ale ⅗ jest nieredukowalne i różni się od ⅔, dlatego druga frakcja nie równa się ⅔.