Historia statystyki wnioskowania, cechy, do czego służy przykłady

Statystyka wnioskowania lub statystyki dedukcyjne to taka, która odstąwa cechy populacji z próbek wyodrębnionych z niej, poprzez szereg technik analizy. W przypadku uzyskanych informacji opracowane są modele, które następnie umożliwiają prognozy dotyczące zachowania wspomnianej populacji.

Dlatego statystyki wnioskowania stały się najważniejszą nauką, która oferuje utrzymanie i instrumenty, których niezliczone dyscypliny wymagają przy podejmowaniu decyzji.

Fizyka, chemia, biologia, inżynieria i nauki społeczne, nieustannie korzystają z tych narzędzi, gdy tworzą swoje modele oraz projektowanie i wdrażają eksperymenty.

[TOC]

Krótka historia wnioskowania statystyki

Statystyki powstały w czasach starożytnych ze względu na potrzebę organizacji rzeczy i optymalizacji zasobów. Przed wynalezieniem pisania przeprowadzono zapisy liczby ludzi i zwierząt gospodarskich, poprzez symbole zapisane w kamieniu.

Później władcy chińscy, babilońscy i egipscy zostawili dane o ilości upraw i liczby mieszkańców, zarejestrowanych na glinianych tabletkach, kolumnach i zabytkach.

Imperium Rzymskie

Kiedy Rzym ćwiczył swoją domenę na Morzu Śródziemnym, władze powszechne było przeprowadzanie spisów powszechnych co pięć lat. W rzeczywistości słowo „statystyczne” pochodzi od włoskiego słowa Statista, Co to znaczy wyrazić.

Równolegle, w Ameryce wielkie imperia pre -kolumbijskie również przyniosły podobne zapisy.

Średniowiecze

W średniowieczu rządy Europy, a także kościół, zarejestrowały własność ziemi. Potem zrobili to samo z narodzinami, chrztami, małżeństwami i śmiercią.

Współczesny wiek

Angielska statystyka John Graunt (1620-1674) jako pierwsza dokonała prognoz na podstawie takich list, takich jak liczba osób umrze z niektórymi chorobami i szacunkową odsetkiem narodzin kobiet i mężczyzn. Dlatego uważa się ojciec demografii.

Współczesny wiek

Później, wraz z nadejściem teorii prawdopodobieństwa, statystyki przestały być zwykłym zbiorem technik organizacyjnych i osiągnęły nieoczekiwany zakres jako nauka predykcyjna.

W ten sposób eksperci byli w stanie.

Charakterystyka

Poniżej mamy najbardziej odpowiednie cechy tej gałęzi statystyki:

- Statystyka wnioskowania Badanie populacji przyjmującej z niej reprezentatywną próbkę.

- Wybór próbki odbywa się w różnych procedurach, najbardziej odpowiednie są te, które losowo wybierają komponenty. Zatem każdy element populacji ma takie samo prawdopodobieństwo, że zostanie wybrany, a wraz z nią unika się niepożądanych uprzedzeń.

Może ci służyć: jak przekonwertować z km/h a m/s? Rozwiązane ćwiczenia

- Aby zorganizować zebrane informacje, wykorzystuje statystyki opisowe.

- W próbce obliczane są zmienne statystyczne, które służą do oszacowania właściwości populacji.

- Statystyki wnioskowania lub dedukcyjne wykorzystują teorię prawdopodobieństwa do badania losowych zdarzeń, to znaczy tych, które powstają przypadkowo. Każde zdarzenie przypisuje się pewne prawdopodobieństwo wystąpienia.

- Zbuduj hipotezy -Posowania - o parametrach populacji i kontrast je, aby wiedzieć, czy są one poprawne, a także oblicza poziom zaufania odpowiedzi, to znaczy oferuje margines błędu. Pierwsza procedura nazywa się Testy hipotez, Podczas gdy margines błędu jest przedział ufności.

Czego jest statystyki opisowe? Aplikacje

Statystyka wnioskowania: niezbędna do podejmowania decyzji i kontroli jakości

Studia w całości populacja może wymagać dużo zasobów w pieniędzmi, czasu i wysiłku. Lepsze jest przyjmowanie reprezentatywnych próbek, które są znacznie łatwiejsze do zarządzania, zbierać za pomocą danych i tworzyć hipotezy lub założenia dotyczące zachowania próbki.

Po ustaleniu hipotez i ich ważności wyniki rozciągają się na populację i są wykorzystywane do podejmowania decyzji.

Pomagają również tworzyć modele tej populacji, aby stworzyć przyszłe projekcje. Dlatego statystyka wnioskowania jest bardzo przydatną nauką dla:

Socjologia i badania demograficzne

Są to idealne pola zastosowania, ponieważ techniki statystyczne mają zastosowanie do pomysłu ustanowienia różnych modeli ludzkich zachowań. Coś, co a priori jest dość skomplikowane, ponieważ interweniują wiele zmiennych.

W polityce wiele jest wykorzystywanych w czasie wyborów, aby poznać tendencję do głosowania elektoratu, w ten sposób partie projektują strategie.

Inżynieria

Metody statystyki wnioskowania są szeroko stosowane w inżynierii, a najważniejszymi zastosowaniami są optymalizacja kontroli jakości i procesy, na przykład poprawa czasów wykonywania zadań, a także w zapobieganiu wypadkom zawodowym.

Gospodarka i administracja biznesowa 

Dzięki metodom dedukcyjnym można przeprowadzić prognozy dotyczące działania firmy, oczekiwanego poziomu sprzedaży, a także pomocy przy podejmowaniu decyzji.

Na przykład twoje techniki można wykorzystać do oszacowania reakcji kupujących na nowy produkt, bliski wprowadzenia na rynek.

Służy również do oceny, jakie są modyfikacje w nawykach konsumpcyjnych ludzi, otrzymują ważne zdarzenia, takie jak epidemia Covid.

Przykłady wnioskowania statystyki

Przykład 1

Prosty dedukcyjny problem statystyczny jest następujący: nauczyciel matematyki jest odpowiedzialny za 5 sekcji algebry podstawowej na uniwersytecie i decyduje się na użycie średniej nut jednej z ich sekcji, aby oszacować średnią ze wszystkich.

Może ci służyć: przybliżony pomiar liczb amorficznych: przykład i ćwiczenieJednak duża populacja może być badana za pomocą reprezentatywnej próbki. Źródło: Pixabay.

Inną możliwością jest wzięcie próbki każdej sekcji, zbadanie jej charakterystyki i rozszerzenie wyników na wszystkie sekcje.

Przykład 2

Kierownik sklepu odzieżowego dla kobiet chce wiedzieć, ile pewnej bluzki zostanie sprzedana w sezonie letnim. Aby to zrobić, przeanalizuj sprzedaż odzieży w pierwszych dwóch tygodniach sezonu, a tym samym określ tendencja.

Podstawowe pojęcia w statystyce wnioskowania

Istnieje kilka kluczowych pojęć, w tym te, które pochodzą z teorii prawdopodobieństwa, która jest niezbędna do jasnego zrozumienia całego zakresu tych technik. Niektóre, jako populacja i próbka, wspominaliśmy już w całym tekście.

Wydarzenie

Zdarzenie lub wydarzenie to coś, co się dzieje, co może mieć kilka wyników. Przykładem zdarzenia może być uruchomienie waluty i są dwa możliwe wyniki: twarz lub pieczęć.

Przykładowa przestrzeń

Jest to zestaw wszystkich możliwych wyników zdarzenia.

Populacja i próbka

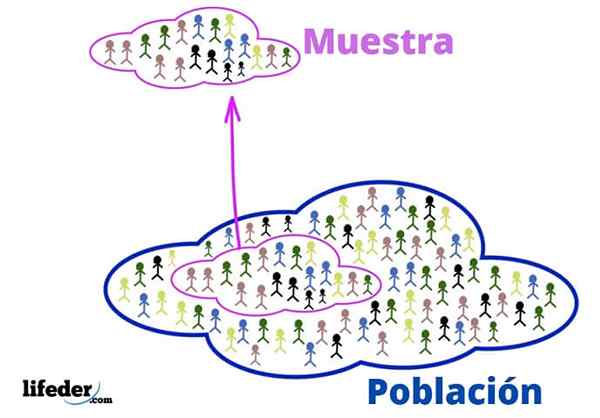Populacja i próbka

Populacja jest wszechświatem do zbadania. Niekoniecznie dotyczą żywych ludzi lub istot, ponieważ populacja, w statystykach, może składać się z przedmiotów lub pomysłów.

Ze swojej strony próbka jest podzbiorem populacji, wyodrębnionej z niej ostrożnie za reprezentatywność.

Próbowanie

Jest to zestaw technik, za pomocą których próbka jest wybierana z danej populacji. Próbkowanie może być losowe, jeśli metody probabilistyczne zostaną użyte do wyboru próbki, czy nie probabilistyczne, jeśli analityk ma własne kryterium selekcji, zgodnie z ich doświadczeniem.

Zmienne statystyczne

Zestaw wartości, które mogą mieć charakterystykę populacji. Są klasyfikowane na kilka sposobów, na przykład mogą być dyskretne lub ciągłe. Również, zgodnie z ich naturą, mogą być jakościowe lub ilościowe.

Rozkłady prawdopodobieństwa

Funkcje prawdopodobieństwa opisujące zachowanie dużej liczby systemów i sytuacji obserwowanych w naturze. Najbardziej znane to dystrybucja Gaussa lub rozkład dzwonka Gaussa i dwumianowy.

Parametry i statystyki 

Teoria oszacowania stwierdza, że ​​istnieje związek między wartościami populacji a wartościami próby pobranej z tej populacji. parametry Są to cechy populacji, których nie wiemy, ale chcemy oszacować: na przykład średnia i odchylenie standardowe.

Ze swojej strony statystyczny są cechami próbki, na przykład jej średniej i standardowej odchylenia.

Na przykład załóżmy, że populacja składa się ze wszystkich młodych ludzi w wieku od 17 do 30 lat społeczności i pożądane jest, aby poznać odsetek osób obecnie w szkolnictwie wyższym. Byłby to parametr populacji, który należy określić.

Może ci służyć: interpolacja liniowa

Aby go oszacować, wybierana jest losowa próbka 50 młodych ludzi, a odsetek z nich studiuje na uniwersytecie lub instytucie szkolnictwa wyższego. Ta proporcja jest statystyką.

Jeśli badanie zostanie przeprowadzone, ustalono, że 63 % z 50 młodych ludzi bada wyżej, jest to szacowana populacja, wykonana z próby.

To jest tylko przykład tego, co mogą zrobić statystyki wnioskowania. Jest znany jako oszacowanie, ale istnieją również techniki przewidywania zmiennych statystycznych, a także podejmowania decyzji.

Hipoteza statystyczna

Jest to domniemanie, które jest dokonane dotyczące wartości średniej i odchylenia standardowego pewnej cechy populacji. O ile populacja nie zostanie całkowicie zbadana, są to nieznane wartości.

Testy hipotez

Czy założenia dotyczące parametrów populacji ważne? Aby to wiedzieć, weryfikuje się, czy wyniki próbki je potwierdzają, czy nie, dlatego konieczne jest zaprojektowanie testów hipotez.

Są to ogólne kroki do wykonania jednego:

Krok 1

Zidentyfikuj rodzaj rozmieszczenia, którego populacja ma przestrzegać.

Krok 2

Podnieś dwie hipotezy, oznaczone jako H_albo i H₁. Pierwszy to Hipoteza zerowa w którym zakładamy, że parametr ma określoną wartość. Drugi jest Alternatywna hipoteza co jest inną wartością niż hipoteza zerowa. Jeśli zostanie to odrzucone, alternatywna hipoteza jest przyjmowana.

Krok 3

Ustalić akceptowalny margines różnicy między parametrem a statystyką. Rzadko będą identyczne, chociaż oczekuje się, że będą bardzo blisko.

Krok 4

Zaproponuj kryterium zaakceptowania lub odrzucenia hipotezy zerowej. W tym celu stosuje się statystykę testową, która może być średnia. Jeśli średnia wartość mieści się w określonych granicach, hipoteza zerowa jest akceptowana, w przeciwnym razie jest odrzucana.

Krok 5

Jako ostatni krok decyduje się, czy hipoteza zerowa jest akceptowana.

Interesujące tematy

Oddziały statystyczne.

Zmienne statystyczne.

Populacja i próbka.

Opisowe statystyki.

Bibliografia

1. Berenson, m. 1985.Statystyki dotyczące administracji i gospodarki, koncepcje i zastosowania. Międzyamerykański redakcja.
2. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
3. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage Learning.
4. Historia statystyki. Odzyskane z: eumed.internet.
5. Ibañez, s. 2010. Matematyka II. Podejście kompetencyjne. Cengage Learning.
6. Levin, r. 1981. Statystyki dla administratorów. Prentice Hall.
7. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.