Wzory i równania błędu próbkowania, obliczenia, przykłady
- 3413
- 1022
- Eliasz Dubiel
On błąd próbkowania albo błąd przykładowy W statystykach jest to różnica między średnią wartością próbki w odniesieniu do średniej wartości całkowitej populacji. Aby zilustrować ten pomysł, wyobraźmy sobie, że całkowita populacja miasta to milion, od którego chcesz jego przeciętne buty, dla których tysiąc ludzi jest przyjmowanych w losowej próbce.
Średnia wielkość wynikająca z próbki niekoniecznie zbiega się z wielkością całkowitej populacji, chociaż jeśli próbka nie jest stronnicza, wartość musi być blisko. Ta różnica między średnią wartością próbki a wartości całkowitej populacji to błąd próbki.
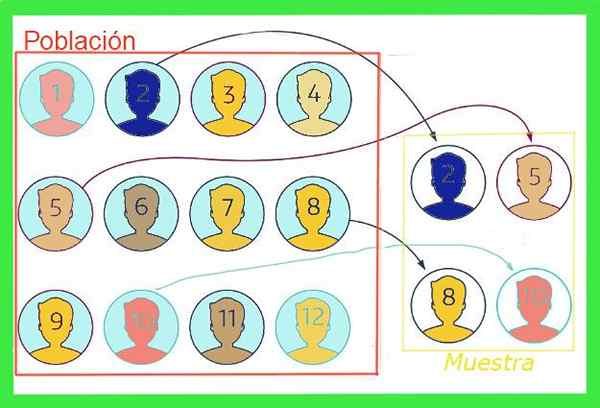
 Rysunek 1. Ponieważ próbka jest podzbiorem całkowitej populacji, średnia próbki ma margines błędu. Źródło: f. Zapata.
Rysunek 1. Ponieważ próbka jest podzbiorem całkowitej populacji, średnia próbki ma margines błędu. Źródło: f. Zapata. Ogólnie rzecz biorąc, średnia wartość całkowitej populacji jest nieznana, ale istnieją techniki zmniejszenia takich błędów i formuł do oszacowania Przykładowy margines błędu które zostanie wystawione w tym artykule.
[TOC]
Wzory i równania
Na wszelki wypadek chcesz poznać średnią wartość pewnej wymiernej funkcji X W populacji wielkości N, ale jak N Duża liczba nie jest opłacalna, aby zbadać całkowitą populację, dlatego przystąpimy do próbka Aleatory wielkościowy N<
Średnia wartość próbki jest oznaczona, a średnia wartość całkowitej populacji oznacza ją dla listu greckiego μ (To czyta Mu lub miu).
Załóżmy, że są zabrane M Całkowite próbki populacji N, Cały równy rozmiar N Ze średnimi wartościami
Te średnie wartości nie będą identyczne i wszystkie będą znajdować się wokół średniej wartości populacji μ. On Przykładowy margines błędu e wskazuje oczekiwane oddzielenie średnich wartości w odniesieniu do Średnia wartość populacji μ w ramach określonego odsetka o nazwie Poziom zaufania γ (Gamma).
Może ci służyć: odwrotność addytywnaOn Standardowy margines błędu ε próbki wielkości N Jest:
ε = σ/√n
Gdzie σ jest odchyleniem standardowym (Pierwiastek kwadratowy wariancji), który jest obliczany w następującym wzorze:
σ = √ [(x -)2/(N - 1)]
Znaczenie Standardowy margines błędu ε jest następujący:
On wartość środkowa uzyskane przez próbkę wielkości N jest rozumiany w przedziale ( - ε, + ε) z poziom zaufania 68,3%.
Jak obliczyć błąd próbkowania
W poprzedniej sekcji podano formułę w celu znalezienia Zakres błędów standard próbki n, gdzie standardowe słowo wskazuje, że jest to margines błędu z 68% zaufaniem.
Wskazuje to, że jeśli pobrano wiele próbek tej samej wielkości N, 68% z nich da średnie wartości w zakresie [ - ε, + ε].
Istnieje prosta zasada, zwana Zasada 68-95-99.7 To pozwala nam znaleźć margines Błąd przykładowy e Dla poziomów ufności 68%, 95% I 99,7% łatwo, ponieważ ten margines wynosi 1⋅ε, 2⋅ε i 3⋅ε odpowiednio.
Dla poziomu ufności γ
Jeśli on Poziom zaufania γ To nie jest żaden z powyższych, więc błąd próbkowania jest odchyleniem standardowym σ pomnożone przez czynnik Zγ, który jest uzyskiwany w następującej procedurze:
1.- Po pierwsze poziom istotności α który jest obliczany z Poziom zaufania γ Poprzez następujący związek: α = 1 - γ
Może ci służyć: twierdzenie Bayesa2.- Następnie musisz obliczyć wartość 1 - α/2 = (1 + γ)/2, co odpowiada normalnej częstotliwości gromadzonej między -∞ i Zγ, W normalnym lub gaussowskim rozkładowi typu F (z), którego definicja można zobaczyć na rycinie 2.
3.- Równanie jest rozwiązane F (Zγ) = 1 - α/2 Poprzez tabele rozkładu normalnego (nagromadzone) F, o poprzez aplikację komputerową, która ma typową odwrotną funkcję Gaussa F-1.
W tym drugim przypadku:
Zγ = g-1(1 - α/2).
4.- Wreszcie stosuje się ten formuła błędu próbkowania z poziomem niezawodności γ:
E = Zγ⋅(σ/√n)
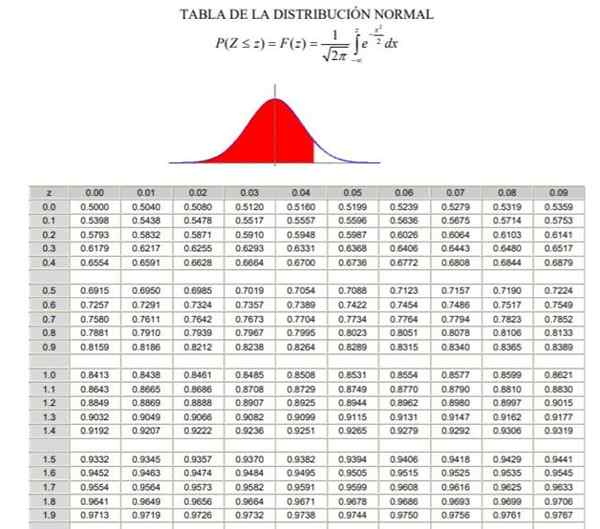 Rysunek 2. Tabela rozkładu normalnego. Źródło: Wikimedia Commons.
Rysunek 2. Tabela rozkładu normalnego. Źródło: Wikimedia Commons. Przykłady
- Przykład 1
Oblicz Standardowy margines błędu Średnia waga próbki 100 noworodków. Obliczenie średniej masy wyniosło = 3100 kg przy odchyleniu standardowym σ = 1500 kg.
Rozwiązanie
On Standardowy margines błędu Jest ε = σ/√n = (1 500 kg)/√100 = 0,15 kg. Co oznacza, że przy tych danych można wywnioskować, że waga 68% noworodków wynosi od 2950 kg do 3.25 kg.
- Przykład 2
Określić margines błędu próbki i oraz zakres wagi 100 noworodków o poziomie ufności 95%, jeśli średnia waga wynosi 3100 kg przy odchyleniu standardowym σ = 1500 kg.
Rozwiązanie
Jeśli Zasada 68; 95; 99.7 → 1⋅ε; 2⋅ε; 3⋅ε, Ty masz:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Innymi słowy, 95% noworodków będzie miało peso od 2800 kg do 3400 kg.
- Przykład 3
Określ zakres pesos noworodków przykładu 1 z 99,7% marginesem ufności.
Może ci służyć: Rhomboid: Charakterystyka, jak wyjąć obwód i obszarRozwiązanie
Błąd próbki z 99,7% zaufaniem jest 3 σ/√n, że dla naszego przykładu jest e = 3 *0,15 kg = 0,45 kg. Stąd wywnioskuje się, że 99,7% noworodków będzie miało peso od 2650 kg do 3550 kg.
- Przykład 4
Określ współczynnik Zγ Dla poziomu niezawodności 75%. Określ margines błędu próbkowania z tym poziomem niezawodności dla sprawy podniesionej w przykładzie 1.
Rozwiązanie
On poziom zaufania Jest γ = 75% = 0,75, które odnosi się do poziom istotności α poprzez związek γ= (1 - α), tak że poziom istotności jest α = 1 - 0,75 = 0,25.
Oznacza to, że skumulowane normalne prawdopodobieństwo między -∞ i Zγ Jest:
P (z ≤ Zγ ) = 1 - 0,125 = 0,875
Co odpowiada wartości Zγ 11503, jak pokazano na rycinie 3.
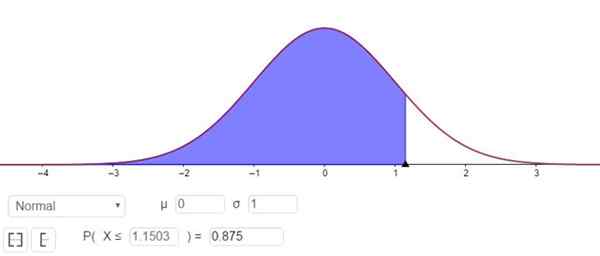 Rysunek 3. Określenie współczynnika Zγ odpowiadającego 75% poziomowi ufności. Źródło: f. Zapata przez Geogebra.
Rysunek 3. Określenie współczynnika Zγ odpowiadającego 75% poziomowi ufności. Źródło: f. Zapata przez Geogebra. Innymi słowy, błąd próbkowania jest E = Zγ⋅(σ/√n)= 1.15⋅(σ/√n).
Po zastosowaniu do przykładu 1 daje błąd:
E = 1,15*0,15 kg = 0,17 kg
Z 75% poziomem ufności.
- Ćwiczenie 5
Jaki jest poziom zaufania, jeśli Zα/2 = 2.4 ?
Rozwiązanie
P (z ≤ zα/2 ) = 1 - α/2
P (z ≤ 2.4) = 1 - α/2 = 0,9918 → α/2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Poziom istotności wynosi:
α = 0,0164 = 1,64%
I wreszcie pozostaje poziom zaufania:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Bibliografia
- Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
- Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
- Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
- Sudman, s.1982. Zadawanie pytań: Praktyczny przewodnik po projektowaniu kwestionariusza. San Francisco. Jossey Bass.
- Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.
- Wonnacott, t.H. i r.J. Wonnacott. 1990. Statystyka wprowadzająca. Ed. Wiley
- Wikipedia. Błąd przykładowy. Źródło: w:.Wikipedia.com
- Wikipedia. Margines błędu. Źródło: w:.Wikipedia.com
- « Historia statystyki wnioskowania, cechy, do czego służy przykłady
- U -Test of Mann - Whitney What Is and kiedy ma zastosowanie, wykonanie, przykład »

