U -Test of Mann - Whitney What Is and kiedy ma zastosowanie, wykonanie, przykład

U -test of Mann - Whitney Jest stosowany do porównania dwóch niezależnych próbek, gdy mają niewiele danych lub nie wykonują normalnego rozkładu. W ten sposób uważa się to za test nie parametryczny, W przeciwieństwie do twojego odpowiednika Test t -Student, to jest używane, gdy próbka jest wystarczająco duża i podąża za rozkładem normalnym.

Frank Wilcoxon proponuje to po raz pierwszy w 1945 r., W przypadku próbek o identycznych rozmiarach, ale dwa lata później został przedłużony w przypadku próbek różnej wielkości przez Henry'ego Manna i D. R. Whitney.

Rysunek 1. Test U Manna - Whitney jest stosowany do porównania niezależnych próbek. Źródło: Pixabay.

Często test jest stosowany w celu sprawdzenia, czy istnieje związek między zmienną jakościową a inną ilością.

Ilustracyjnym przykładem jest przyjęcie zestawu osób nadciśnieniowych i wyodrębnienie dwóch grup, do których codzienne dane ciśnienia krwi są rejestrowane przez miesiąc.

Do jednej grupy leczenie a, a druga jest stosowana, leczenie b. Tutaj ciśnienie krwi jest zmienną ilościową, a rodzaj leczenia jest jakościowe.

Chcesz wiedzieć, czy mediana, a nie średnia, zmierzonych wartości jest statystycznie równa czy inna, aby ustalić, czy istnieje różnica między obiema zabiegami. Aby uzyskać odpowiedź, zastosowany jest Wilcoxon lub U -est of Mann - Whitney.

[TOC]

Podejście problemowe w testach U Manna - Whitney

Innym przykładem, w którym można zastosować test, jest następujący:

Załóżmy, że chcesz wiedzieć, czy spożywanie napojów bezalkoholowych różni się znacznie w dwóch regionach kraju.

Jeden z nich nazywa się region A i drugi region B. Przeprowadzana jest zapis litrów spożywanych w dwóch próbkach: jedna z 10 osób dla regionu A i kolejne z 5 osób dla regionu B.

Dane są następujące:

-Region a: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

-Region b: 12,14, 11, 30, 10

Poniższe pytanie jest postawione:

Czy spożywanie napojów bezalkoholowych (y) zależy od regionu (x)?

Zmienne jakościowe w porównaniu do zmiennych ilościowych

-Zmienna jakościowa x: Region

-Zmienna ilościowa i: Zużycie gazowe

Jeśli ilość spożywanych litrów jest taka sama w obu regionach, wniosek będzie taki, że nie będzie zależności między dwiema zmiennymi. Sposobem na poznanie jest porównywanie średniej lub mediany trendu dla dwóch regionów.

Normalny przypadek

Jeśli dane były zgodne z rozkładem normalnym, podniesione są dwie hipotezy: zerowa H0 i alternatywa H1 poprzez porównanie średnich:

Może ci służyć: godne uwagi produkty

-H0: Nie ma różnicy między średnią z dwóch regionów.

-H1: Środki obu regionów są różne.

Przypadek bez - normalnej tendencji

Wręcz przeciwnie, jeśli dane nie są zgodne z rozkładem normalnym lub po prostu próbka jest bardzo mała, zamiast porównywać średnią, którą można by porównać Mediana z dwóch regionów.

-H0: Nie ma różnicy między medianą dwóch regionów.

-H1: Mediany obu regionów są różne.

Jeśli mediany się pokrywają, wówczas hipoteza zerowa jest spełniona: nie ma związku między zużyciem sody a regionem.

A jeśli nastąpi odwrotnie, alternatywna hipoteza jest prawdziwa: istnieje związek między konsumpcją a regionem.

To w tych przypadkach, w których wskazany jest test U Manna - Whitney.

Próbki próbki lub nieczyste

Poniższa ważna kwestia, aby zdecydować, czy zastosowano test U Manna Whitneya, jest to, czy liczba danych w obu próbkach jest identyczna, co jest równoważne stwierdzeniu, że są one jednocześnie.

Jeśli dwie próbki zostaną sparowane, miałaby zastosowanie oryginalna wersja Wilcoxona. Ale jeśli nie, jak dotyczy tego przykładu, zastosowano zmodyfikowany test Wilcoxona, który jest dokładnie testem U Whitneya.

Charakterystyka testu Mann Whitney U

Test U Manna -Whitney Nieparametryczny test, który ma zastosowanie do próbek, które nie są zgodne z rozkładem normalnym lub z kilkoma danymi. Ma następujące cechy:

1.- Porównaj mediany

2.- Prace na zamówionych zakresach

3.- Jest mniej potężny, zrozumienie przez moc prawdopodobieństwo odrzucenia hipotezy zerowej, gdy w rzeczywistości jest to fałszywe.

Biorąc pod uwagę te cechy, test U Manna - Whitney jest stosowany, gdy:

-Dane są niezależne

-Nie podążają za normalnym rozkładem

-Hipoteza zerowa H0 jest akceptowana, jeśli medium dwóch próbek pokrywa się: MA = MB

-Alternatywna hipoteza H1 jest akceptowana, jeśli medium dwóch próbek różni się: Ma ≠ Mb

Mann Formuła - Whitney

Zmienna U to kontrastowa okazja stosowana w teście Mann - Whitney i jest zdefiniowana:

U = min (ua, ub)

Oznacza to, że u jest najmniejszym wartościami między UA i UB, zastosowane do każdej grupy. W naszym przykładzie byłoby to dla każdego regionu: A O B.

Zmienne UA i UB są zdefiniowane i obliczane zgodnie z następującym wzorem:

Ua = nb + na (Na +1)/2 - ra

UB = NB + NB (NB +1)/2 - RB

Może ci służyć: redukcja podobnych terminów

Tutaj wartości NA i NB są rozmiarem próbek odpowiadających odpowiednio regionom A i B, a z drugiej strony RA i RB są Suma zasięgu że zdefiniujemy poniżej.

Kroki w celu zastosowania testu

1.- Zamów wartości dwóch próbek.

2.- Przypisz zakres zamówień do każdej wartości.

3.- Popraw istniejące ligatury w danych (powtarzane wartości).

4.- Oblicz RA = suma zakresów próbki A.

5.- Znajdź rb = suma zakresów próbki B.

6.- Określ wartość UA i UB, zgodnie z formułami podanymi w poprzednim rozdziale.

7.- Porównaj UA i UB, a niewielka z nich jest przypisana do statystyki lub eksperymentalnej (to znaczy danych) w porównaniu z statystyką teoretyczną lub normalną.

Praktyczne zastosowanie zastosowania

Teraz stosujemy wspomniane wyżej na problemie wcześniej podniesionej sody:

Region A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

Region B: 12,14, 11, 30, 10

W zależności od tego, że środki obu próbek są statystycznie takie same lub różne, przystępujemy do akceptowania lub odrzucania hipotezy zerowej: nie ma związku między zmienną a x, to znaczy, że zużycie sody nie zależy od regionu:

H0: MA = MB

H1: Ma ≠ Mb

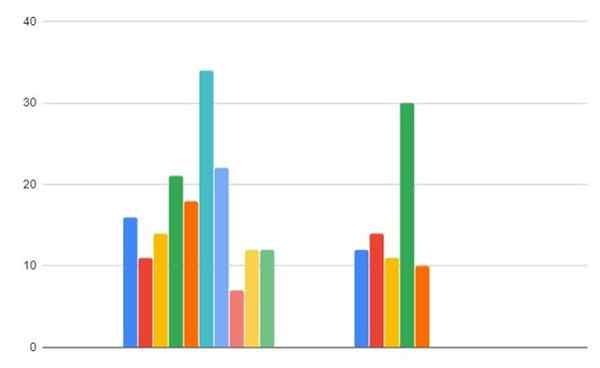Rysunek 2. Dane dotyczące konsumpcji gazowej w regionach A i B. Źródło: f. Zapata.

- Krok 1

Prowadzimy zamówienie danych wspólnie dla dwóch próbek, zamawiając wartości od najmniejszej do największej:

Zauważ, że wartość 11 pojawia się 2 razy (raz w każdej próbce). Pierwotnie ma pozycje lub zakresy 3 i 4, ale nie w celu przeceniania ani nie doceniania jednej lub drugiej średniej wartości jest wybierana jako zakres, czyli 3,5.

Podobnie, wartość 12 jest postępowana, która jest powtarzana trzykrotnie z zakresami 5, 6 i 7.

Cóż, wartość 12 przypisuje się średni zakres 6 = (5+6+7)/3. I to samo dla wartości 14, która ma podwiązanie (pojawia się w obu próbkach) w pozycjach 8 i 9, przypisany jest średni zakres 8.5 = (8+9)/2.

- Krok 2

Dane dla regionu A i B są następnie oddzielone ponownie, ale teraz ich odpowiednie zakresy są przypisywane w innym rzędzie:

Region a

Region b

Zakresy RB są uzyskiwane z sum elementów drugiego rzędu dla każdego przypadku lub regionu.

Krok 3

Obliczane są odpowiednie wartości UA i UB:

UA = 10 × 5 + 10 (10 + 1)/2 - 86 = 19

UB = 10 × 5 + 5 (5 + 1)/2 -34 = 31

Wartość eksperymentalna u = min (19, 31) = 19

Krok 4

Teoretyk ma postępować zgodnie z rozkładem normalnym N z parametrami podawanymi wyłącznie przez wielkość próbek:

Może ci służyć: liczby irracjonalne: historia, właściwości, klasyfikacja, przykłady

N ((Na⋅NB) /2, √ [nb (Na + NB +1) /12])

Aby porównać zmienną lub uzyskaną eksperymentalnie, z teoretyczną konieczne jest dokonanie zmiennej zmiany. Przechodzi od zmiennej lub eksperymentalnej do jej wartości typowe, które zostanie nazwane Z, Aby móc porównać z rozkładem normalnym typem.

Zmiana zmienna jest następująca:

Z = (u - na.Nb / 2) / √ [na. NB (Na + NB + 1) / 12] 

Należy zauważyć, że dla zmiany zmiennej zastosowano parametry rozkładu teoretycznego dla U. Następnie nowa zmienna Z, która jest hybrydą między teoretyczną i eksperymentalną lub normalną rozkładem N (0,1).

Kryteria porównawcze

Jeśli Z ≤ Zα ⇒ Hipoteza zerowa H0 jest akceptowana

Tak Z> Zα ⇒ Hipoteza zerowa H0 jest odrzucana

Wartości krytyczne typowe zależne od poziomu wymaganego poziomu zaufania, na przykład dla poziomu zaufania α = 0,95 = 95%, który jest najbardziej zwykle, ma wartość krytyczną Zα = 1,96.

Dla danych pokazanych tutaj:

Z = (u - nb / 2) / √ [nb (Na + nb + 1) / 12] = -0,73

Który jest poniżej wartości krytycznej 1.96.

Następnie ostatecznym wnioskiem jest to, że hipoteza zerowa jest akceptowana:

Nie ma różnicy w spożyciu sody między regionami A i B.

Kalkulatory online dla testu U Manna - Whitney

Istnieją konkretne programy do obliczeń statystycznych, w tym SPSS i minitab, ale programy te są opłacane, a ich użycie nie zawsze jest proste. Jest tak, ponieważ dają tak wiele opcji, że jego użycie jest praktycznie zarezerwowane dla ekspertów ds. Statystyki.

Na szczęście istnieje kilka bardzo precyzyjnych, bezpłatnych i prostych programów online, które pozwalają między innymi na testy U -Whitneya.

Te programy to:

-Statystyka nauk społecznych (Socistatistics.com), który ma zarówno test U Whitneya, jak i Wilcoxona w przypadku zrównoważonych lub sparowanych próbek.

-Statystyka terapii AI (AI-terapia.com), który ma kilka zwykłych opisowych testów statystycznych.

-Statystyczny do użycia (fizyka.CSBSJU.EDU/Stats), jeden z najstarszych, więc twój interfejs może wyglądać na przestarzały, chociaż jest to bardzo wydajny program bezpłatny.

Bibliografia

1. Dietrichson. Metody ilościowe: Test zakresu zakresów. Odzyskane z: BookDown.org
2. Marín J p. Przewodnik SPSS: Analiza i procedury w testach nieparametrycznych. Odzyskane z: halweb.UC3M.Jest
3. Usal MOOC. Test nieparametryczny: U of Mann - Whitney. Odzyskane z: YouTube.com
4. Wikipedia. U -test of Mann - Whitney. Odzyskane z: jest.Wikipedia.com
5. Xlstat. Centrum pomocy. Samouczek testowy Manna - Whitney in Excel. Odzyskane z: pomoc.XLSAT.com