Zgrupowane przykłady danych i rozstrzygnięte ćwiczenie

zgrupowane dane Są tymi, którzy sklasyfikowali w kategorie lub zajęcia, przyjmując jako kryteria ich częstotliwość. Odbywa się to w celu uproszczenia zarządzania dużymi ilościami danych i ustanowienia ich trendów.

Po zorganizowaniu w tych klasach dla ich częstotliwości dane stanowią Rozkład częstotliwości, z których informacje o użyteczności są wyodrębnione przez jego cechy.

Rysunek 1. Za pomocą zgrupowanych danych możesz budować grafikę i obliczyć parametry statystyczne, które opisują trendy. Źródło: Pixabay.

Następnie zobaczymy prosty przykład zgrupowanych danych:

Załóżmy, że mierzy się pozycja 100 studentek, wybranych spośród wszystkich podstawowych kursów fizyki uniwersytetu i uzyskano następujące wyniki:

Otrzymane wyniki podzielono na 5 klas, które pojawiają się w lewej kolumnie.

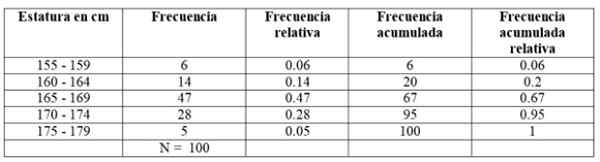
Pierwsza klasa, między 155 a 159 cm, ma 6 uczniów, druga klasa 160 - 164 cm ma 14 uczniów, trzecia klasa od 165 do 169 cm jest ta z największą liczbą członków: 47. Następnie podążaj za klasą 170-174 cm z 28 uczniami, a wreszcie od 175 do 179 cm z zaledwie 5.

Liczba członków każdej klasy jest dokładnie częstotliwość albo Absolutna frecuencja I dodając je wszystkie, otrzymano całkowitą dane, które w tym przykładzie wynosi 100.

[TOC]

Charakterystyka rozkładu częstotliwości

Częstotliwość

Jak widzieliśmy, częstotliwość jest liczba razy powtarzana. Oraz w celu ułatwienia obliczeń właściwości rozkładu, takich jak średnia i wariancja, zdefiniowane są następujące ilości:

-Zgromadzona częstotliwość: Uzyskuje się go przez dodanie częstotliwości klasy z przednią częstotliwością nagromadzoną. Pierwsza ze wszystkich częstotliwości pokrywa się z częstotliwością omawianego przedziału, a ostatnia to całkowita liczba danych.

-Częstotliwość względna: Jest to obliczane przez dzielenie bezwzględnej częstotliwości każdej klasy przez całkowitą liczbę danych. A jeśli mnożą się przez 100, masz procentową częstotliwość.

Może ci służyć: funkcje wektorowe

-Nagromadzona częstotliwość względna: Jest to suma względnych częstotliwości każdej klasy z poprzednimi zgromadzonymi. Ostatnia z skumulowanych częstotliwości względnych musi być równa 1.

W naszym przykładzie częstotliwości są takie:

Granice

Wywołują ekstremalne wartości każdej klasy lub przedziału Limity klasy. Jak widzimy, każda klasa ma niższy limit i jeden większy. Na przykład pierwsza klasa badań dotyczących stwierdzeń ma granicę mniejszą niż 155 cm i jedną większą niż 159 cm.

Ten przykład ma granice, które są jasno zdefiniowane, ale jest to możliwe.

Granice

Wysokość jest zmienną ciągłą, więc można uznać, że pierwsza klasa faktycznie zaczyna się w 154.5 cm, ponieważ poprzez zaokrąglanie tej wartości do najbliższej liczby całkowitej uzyskuje się 155 cm.

Ta klasa obejmuje wszystkie wartości do 159.5 cm, ponieważ z tego statystyki są zaokrąglone do 160.0 cm. Postawa 159.7 cm należy już do następnej klasy.

Prawdziwe granice klasy tego przykładu to w CM:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplituda

Szerokość klasy uzyskuje się przez odejmowanie granic. W pierwszym przedziale naszego przykładu masz 159.5 - 154.5 cm = 5 cm.

Czytelnik może sprawdzić, czy dla innych przedziałów przykładu amplituda również wynika z 5 cm. Warto jednak zauważyć, że dystrybucje można zbudować z odstępami o różnej amplitudzie.

Może ci służyć: reguła t: Charakterystyka, tak że jest przykłady

Marka klasowa

Jest to średni punkt przedziału i jest uzyskiwany przez średnią między górną granicą a dolną granicą.

W naszym przykładzie marka pierwszej klasy to (155 + 159)/2 = 157 cm. Czytelnik może sprawdzić, czy pozostałe marki klasy to: 162, 167, 172 i 177 cm.

Określenie marek klasowych jest ważne, ponieważ są one niezbędne do znalezienia średniej arytmetycznej i wariancji rozkładu.

Miary centralnej tendencji i dyspersji danych zgrupowanych

Najczęściej stosowanymi miarami tendencji centralnej są średnia, mediana i moda i opisują właśnie tendencję danych do grupowania wokół określonej wartości centralnej.

Połowa

Jest to jedna z głównych środków tendencji centralnych. W zgrupowanych danych średnia arytmetyczna można obliczyć za pomocą wzoru:

 Gdzie:

-X to średnia

-F_Siema to częstotliwość klasy

-M_Siema To jest marka klasowa

-G to liczba klas

-n to całkowita liczba danych

Mediana

W przypadku mediany musisz zidentyfikować przedział, w którym znajduje się obserwacja N/2. W naszym przykładzie ta obserwacja to numer 50, ponieważ istnieje w sumie 100 danych. Ta obserwacja jest w przedziale 165-169 cm.

Następnie musisz interpolować, aby znaleźć wartość numeryczną, która odpowiada tej obserwacji, dla której stosuje się formułę:

Gdzie:

-C = szerokość przedziału, w której znajduje się mediana

-B_M = Dolna granica przedziału, do którego należy mediana

-F_M = Ilość obserwacji zawartych w środkowym przedziale

-N/2 = połowa wszystkich danych

-F_BM = Całkowita liczba obserwacji przed środkowym odstępem

Moda

Dla mody zidentyfikowana jest klasa modalna, która zawiera większość obserwacji, których marka klasowa jest znana.

Może ci służyć: sześciokątna piramida

Wariancja i odchylenie standardowe

Wariancja i odchylenie standardowe są miarami dyspersji. Jeśli oznaczamy wariancję z S² Oraz do odchylenia standardowego, które jest pierwiastkiem kwadratowym wariancji jako S, dla danych zgrupowanych odpowiednio:

I

Ćwiczenie rozwiązane

W celu rozmieszczenia pozycji studentów uniwersytetów zaproponowanych na początku oblicz wartości:

a) średnia

b) medium

c) Moda

d) wariancja i odchylenie standardowe.

Rysunek 2. Jeśli chodzi o wiele wartości, takich jak statystyki dużej grupy uczniów, preferowane jest grupowanie danych w klasach. Źródło: Pixabay.

Rozwiązanie

Zbudujmy następującą tabelę, aby ułatwić obliczenia:

Poprzez wyrażenie przeciętnej grupy zgrupowanej powyżej:

Zastępowanie wartości i bezpośrednio przeprowadzanie suma:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) /100 cm =

= 167.6 cm

Rozwiązanie b

Odstęp, do którego należy mediana, wynosi 165-169 cm, ponieważ najczęściej jest to przedział.

Zidentyfikujmy każdą z tych wartości w przykładzie za pomocą tabeli 2:

C = 5 cm (patrz sekcja amplitudy)

B_M = 164.5 cm

F_M = 47

N/2 = 100/2 = 50

F_BM = 20

Zastąpienie w formule:

Rozwiązanie c

Odstęp zawarty w większości obserwacji wynosi 165-169 cm, którego marka klasowa wynosi 167 cm.

Rozwiązanie d

Rozszerzamy poprzedni tabelę, dodając dwie dodatkowe kolumny:

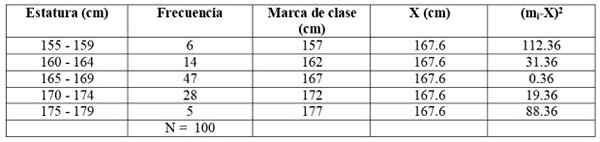
Stosujemy formułę:

I opracowujemy sumę:

S² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Dlatego:

S = √21.35 cm² = 4.6 cm

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
3. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
4. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
5. Spiegel, m. 2009. Statystyka. Seria Schaum. 4 Ta. Wydanie. McGraw Hill.
6. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.