Rozkład chi-kwadrat (χ²), jak jest obliczany, przykłady

Dowód Chi kwadrat albo Ji-Square (χ², Gdzie χ jest literą grecką zwaną „chi”) służy do określenia zachowania określonej zmiennej, a także gdy chcesz wiedzieć, czy dwie lub więcej zmiennych jest statystycznie niezależne.

Aby sprawdzić zachowanie zmiennej, test zostanie wywołany Chi Square Test regulacji. Wiedzieć, czy dwie lub więcej zmiennych jest statystycznie niezależne od testu, są wywoływane Chi Square of Independence, nazywane również awaryjności.

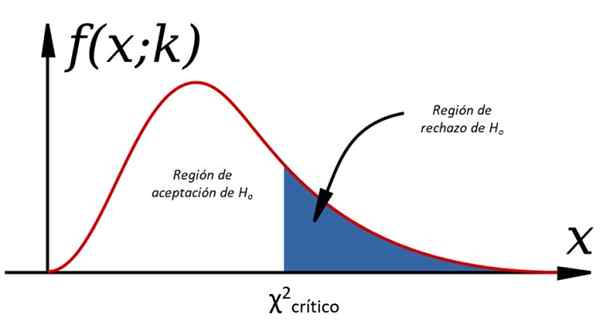
Rysunek 1. Testy hipotez za pośrednictwem chi cuadrado

Dowody te są częścią statystycznej teorii decyzji, w której badana jest populacja i podejmowane są decyzje, analizując jedną lub kilka próbek wyodrębnionych z niej. W tym celu konieczne jest przyjęcie pewnych założeń dotyczących zmiennych, zwanych hipoteza, które mogą być pewne, ale nie.

Istnieją pewne testy, aby kontrastować te hipotety i ustalić, które są prawidłowe, w ramach pewnego marginesu zaufania, w tym test chi-kwadrat, który można zastosować do porównania dwóch i większości populacji.

Jak zobaczymy, zwykle uwzględniane są dwa rodzaje hipotez na temat pewnego parametru populacji w dwóch próbkach: hipoteza zerowa, zwana h_albo (próbki są niezależne), a alternatywna hipoteza, oznaczona jako H₁, (próbki są skorelowane), co jest sprzeczne z tym.

[TOC]

Kiedy jest używany test chi-kwadrat?

Test Chi Square dotyczy zmiennych opisujących cechy, takie jak płeć, status cywilny, grupa krwi, kolor oczu i preferencje różnego rodzaju.

Test został zaprojektowany w razie potrzeby:

-Sprawdź, czy rozkład jest odpowiedni do opisania zmiennej, która jest nazywana dobroć regulacji. Poprzez test kwadratowy Chi możesz wiedzieć, czy istnieją znaczące różnice między wybranym rozkładem teoretycznym a rozkładem częstotliwości.

-Wiedz, czy dwie zmienne x i y są niezależne od statystycznego punktu widzenia. To jest znane jako Test niezależności.

Ponieważ dotyczy zmiennych jakościowych lub kategorycznych, test chi Square jest szeroko stosowany w naukach społecznych, administracji i medycynie.

Warunki do zastosowania

Istnieją dwa ważne wymagania, aby go poprawnie zastosować:

Może ci służyć: jaki jest związek między obszarem Rhombusa a prostokątem?

-Dane muszą być pogrupowane na częstotliwości.

-Próbka musi być wystarczająco duża, aby rozkład kwadratowy Chi był prawidłowy, w przeciwnym razie jego wartość jest przeszacowana i powoduje odrzucenie hipotezy zerowej, gdy tak nie powinno być.

Ogólna zasada jest taka, że ​​jeśli w zgrupowanych danych pojawi się częstotliwość o wartości mniejszej niż 5, nie jest używana. Jeśli istnieje więcej niż jedna częstotliwość mniejsza niż 5, należy je połączyć w jednym, aby uzyskać częstotliwość o wartości liczbowej większej niż 5.

Dystrybucja Chi Square

χ² Jest to ciągły rozkład prawdopodobieństwa. W rzeczywistości istnieją różne krzywe, w zależności od parametru k zwany stopnie swobody losowo.

Jego właściwości to:

-Obszar pod krzywą jest równy 1.

-Wartości χ² Są pozytywne.

-Rozkład jest asymetryczny, to znaczy ma uprzedzenie.

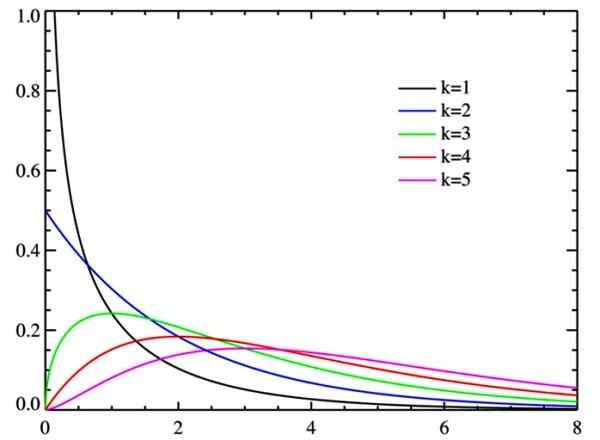Rysunek 2. Rozkład kwadratowy Chi dla stopni wolności. Źródło: Wikimedia Commons.

Stopnie swobody

Wraz ze wzrostem stopnia swobody rozkład chi-kwadrat ma tendencję do normy, jak widać na rysunku.

Dla danego rozkładu stopnie swobody są określane przez Tabela awaryjna, który jest tabelą, w której rejestrowane są obserwowane częstotliwości zmiennych.

Jeśli stół ma F szeregi i C kolumny, wartość k Jest:

K = (F - 1) ⋅ (C - 1)

Formuła hipotezy

Gdy test kwadratowy Chi jest dostosowywany, sformułowane są następujące hipotezy:

-H_albo: zmienna x ma rozkład prawdopodobieństwa f (x) z określonymi parametrami i₁, I₂… , I_P

-H₁: X ma inny rozkład prawdopodobieństwa.

Rozkład prawdopodobieństwa zakładany w hipotezie zerowej może być na przykład dobrze znany rozkład normalny, a parametry byłyby średnie μ i odchylenie standardowe σ.

Ponadto hipoteza zerowa jest oceniana z pewnym poziomem istotności, to znaczy miary błędu, który zostałby popełniony podczas odrzucania go.

Zasadniczo poziom ten jest ustalany w wysokości 1 %, 5 % lub 10 % i im niższy wynik testu, tym bardziej niezawodne.

Może ci służyć: Mumm

A jeśli zastosowano test zwrotności chi Square, który, jak powiedzieliśmy, służy weryfikacji niezależności między dwiema zmiennymi x i y, hipotezy to:

-H_albo: Zmienne x i y są niezależne.

-H₁: X i y są zależne.

Ponownie konieczne jest określenie poziomu istotności, aby poznać miarę błędu podczas podejmowania decyzji.

Jak obliczane są statystyki chi-kwadrat?

Statystyki chi Square są obliczane w następujący sposób:

Symbol ∑ oznacza „podsumowanie”, które musimy zrobić o wskazanym wyrażeniu ułamkowym.

Suma jest przeprowadzana z pierwszej klasy I = 1 do ostatniej, czyli i = k.

Oprócz:

-F_albo Jest to obserwowana częstotliwość (pochodzi z uzyskanych danych).

-F_I Jest to oczekiwana lub teoretyczna częstotliwość (konieczne jest obliczenie jej na podstawie danych).

Aby zaakceptować lub odrzucić hipotezę zerową, χ oblicza się² Dla zaobserwowanych danych i porównuje z wartością o nazwie Chi Critical Square, To zależy od stopni wolności k i poziom istotności α:

χ²_krytyczny =  χ²_{K, α}

Jeśli na przykład chcemy wykonać test z poziomem istotności 1 %, to α = 0.01, jeśli będzie to z 5%, to α = 0.05 i tak dalej. P, parametr rozkładu, taki jak:

P = 1 - α

Te krytyczne wartości kwadratowe są określane przez tabele zawierające wartość skumulowanego obszaru. Na przykład dla k = 1, który reprezentuje 1 stopień swobody i α = 0.05, równoważny p = 1-.05 = 0.95, wartość χ² To jest 3.841.

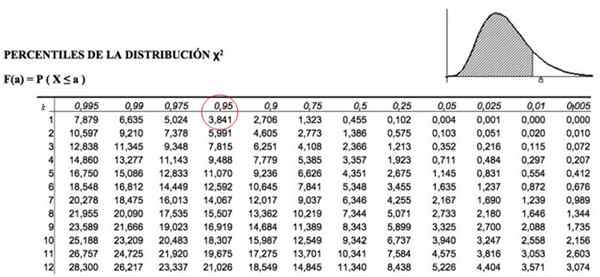Rysunek 3. Tabela wartości rozkładu kwadratowego chi. Źródło: f. Zapata.

Kryteria akceptacji prądu przemiennego_albo

Kryteria zaakceptowania h_albo Jest:

-Tak χ² < χ²_krytyczny  H_albo, W przeciwnym razie jest odrzucony (patrz rysunek 1).

Przykład obliczeń

W poniższej aplikacji test Chi Square zostanie wykorzystany jako test niezależności.

Załóżmy, że naukowcy chcą wiedzieć, czy preferencje czarnej kawy są powiązane z gatunkiem osoby, i określić odpowiedź z poziomem istotności α = 0.05.

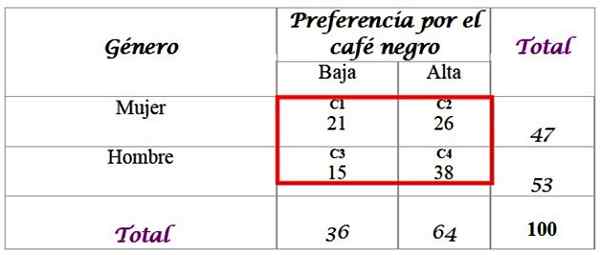
Może ci służyć: zewnętrzne alternatywne kąty: Ćwiczenia i ćwiczenia rozwiązane

W tym celu dostępna próbka 100 osób i ich odpowiedzi są dostępne:

Krok 1

Ustal hipotezy:

-H_albo: Płeć i preferencje dla czarnej kawy są niezależne.
-H₁: Gust czarnej kawy jest związany z gatunkiem osoby.

Krok 2

Oblicz oczekiwane częstotliwości dystrybucji, dla których wymagana jest całkowita dodana w ostatnim wierszu i w prawej kolumnie. Każda komórka w czerwonej polu ma oczekiwaną wartość F_I, który jest obliczany przez pomnożenie całkowitej jego wiersza R przez całą kolumnę C, podzieloną przez całkowitą próbkę n:

F_I = (F x c) /n

Wyniki są następujące dla każdej komórki:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Krok 3

Następnie musisz obliczyć statystykę chi cuadrado dla tego rozkładu, zgodnie z podaną formułą:

χ²= [(21–16.92)² ÷ 16. 92] + [(26–30.08)² ÷ 30.08] + [(15–19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

Krok 4

Określić χ²_krytyczny, Wiedząc, że zarejestrowane dane wynoszą f = 2 rzędy i c = 2 kolumny, dlatego liczba stopni swobody wynosi:

K = (2-1) ⋅ (2-1) = 1.

Co oznacza, że ​​musimy spojrzeć w tabeli pokazanej powyżej wartości χ²_{K, α} = χ²_{1; 0.05} , który jest:

χ²_krytyczny = 3.841

Krok 5

Porównaj wartości i zdecyduj:

χ² = 2.9005

χ²_krytyczny = 3.841

Od χ² < χ²_krytyczny Hipoteza zerowa jest akceptowana i stwierdzono, że preferencje dla czarnej kawy nie są powiązane z gatunkiem osoby, przy poziomie istotności 5%.

Bibliografia

1. Chi Square Test dla niezależności. Odzyskany z: saylordotorg.Github.Io.
2. Med Wave. Statystyki zastosowane do nauk o zdrowiu: test JI-kwadrat. Odzyskany z: Medwave.Cl.
3. Prawdopodobieństwa i statystyki. Test dobroci korekty SHI Square. Źródło: prawdopodobieństwa i.com.
4. TRIOLA, m. 2012. Statystyka podstawowa. 11. Wydanie. Addison Wesley.
5. Unam. Test Chi Square. Odzyskany z: doradczy.Cuautitlan2.Unam.MX.