Historia statystyki opisowej, cechy, przykłady, koncepcje

Opisowe statystyki Jest to oddział statystyk, który zajmuje się gromadzeniem i organizowaniem informacji o zachowaniu systemów z wieloma elementami, ogólnie znanymi jako nazwa populacja.

W tym celu wykorzystuje techniki numeryczne i graficzne, za pomocą których przedstawia informacje, bez przewidywania lub wniosków na temat populacji, w której przychodzi.

Statystyka opisowa jest uważana za organizowanie i wygodne przedstawienie informacji

[TOC]

Historia

Podeszły wiek

Statystyki ma swoje pochodzenie w ludzkiej potrzebie zorganizowania niezbędnych informacji dla jego przetrwania i dobrego samopoczucia, a także zapewnienia zdarzeń, które na to wpływają. Wielkie cywilizacje starożytności pozostawiły zapisy osadników, zebrane podatki, liczbę upraw i wielkość armii.

Na przykład podczas jego długiego panowania, Ramsesa II (1279-1213 do.C) nakazał spis ludności i mieszkańców w Egipcie, który do tego czasu miał około 2 milionów mieszkańców.

Podobnie Biblia, którą Mojżesz wykonał spis ludności, aby wiedzieć, ilu żołnierzy miało dwanaście plemion Izraela.

Również w przypadku starożytnych greckich liczby ludzi i zasobów. Rzymianie, godne uwagi ze swojej wysokiej organizacji, okresowo rejestrowali populację, przygotowując spis ludności co pięć lat, w tym terytoria i zasoby.

renesans

Po upadku Rzymu ważne zapisy statystyczne były przestraszone, aż do przybycia renesansu, gdy pojawia się statystyki.

Kulminacją XVII wieku narodziła się teoria prawdopodobieństwa, w wyniku skłonności ludzi do hazardu, która zapewniła statystyki matematyczne rygor, który uczynił z niego naukę samodzielnie.

Współczesny wiek

Nowy impuls przyszedł z teorią błędów i minimalnych kwadratów w dziewiętnastym wieku, który był zgodny z metodą korelacji między zmiennymi, aby ilościowo ocenić związek między nimi.

Aż do wreszcie, w XX wieku, statystyki rozszerzyły się na każdą gałąź nauki i inżynierii jako niezbędne narzędzie w rozwiązywaniu problemów.

Charakterystyka statystyki opisowej

Statystyka opisowa charakteryzuje się:

- Organizuj informacje zebrane w danych i grafice. Wykresy mogą być różnorodne: histogramy, wielokąty częstotliwości, schematy w kształcie ciasta,.

- Rozpowszechniać dane w zakresie częstotliwości, aby ułatwić zarządzanie. Użyj arytmetyki, aby znaleźć najbardziej reprezentatywne wartości danych, poprzez środki centralne, a także przeanalizować ich dyspersję.

- Określić kształt rozkładów, ich symetria, jeśli są one wyśrodkowane lub stronnicze, a jeśli są skierowane lub raczej spłaszczone.

Może ci służyć: niejawne pochodne: jak są one rozwiązane i rozwiązane ćwiczenia

Czego jest statystyki opisowe?

Ilekroć jest to konieczne.

Następnie wspominamy o niektórych przykładach:

Gospodarka

Statystyka opisowa dotyczy rejestracji i organizacji danych o populacjach i ich wieku, dochodach, inwestycjach, zyskach i wydatkach. W ten sposób rządy i instytucje planują ulepszenia i odpowiednio inwestują.

Dzięki pomocy monitorujesz zakupy, sprzedaż, zwroty i wydajność usług. Z tego powodu statystyki są niezbędne w podejmowaniu decyzji.

Fizyka i mechaniczne

Fizyka i mechanika wykorzystują statystyki do badania środowisk ciągłych, które składają się z dużej liczby cząstek, takich jak atomy i cząsteczki. Okazuje się, że nie można monitorować każdego z nich osobno.

Ale badając globalne zachowanie systemu (na przykład część gazu) z makroskopowego punktu widzenia, można znaleźć średnie i zdefiniować zmienne makroskopowe, aby poznać jego właściwości. Przykładem tego jest kinetyczna teoria gazów.

Medycyna

Jest to niezbędne narzędzie podczas monitorowania chorób, od jego początków i podczas ewolucji, a także skuteczności leczenia.

Statystyki opisujące wskaźniki zachorowalności, gojenia, czasów inkubacji lub rozwoju choroby, wiek, w którym zwykle się pojawia i dane stylowe, są konieczne przy projektowaniu najbardziej skutecznych metod leczenia.

Odżywianie

Jednym z wielu zastosowań statystyk opisowych jest rejestracja i zamówienie danych na temat konsumpcji żywności w różnych populacjach: ich ilość, jakość i które są najczęściej spożywanymi, wśród wielu innych obserwacji, które eksperci interesują.

Przykłady statystyki opisowej

Below we will see some examples that illustrate how useful the tools of descriptive statistics are to help make decisions:

Przykład 1

Aby ulepszyć szkolne jadalnia, wymagane są informacje o użytkownikach. Źródło: Wikimedia Commons.

Władze edukacyjne o ulepszeniach instytucjonalnych krajowych. Załóżmy, że wdroży nowy system szkolnych jadalni.

W tym celu konieczne jest posiadanie danych o populacji studentów, na przykład liczba uczniów na ocenę, ich wiek, płeć, wysokość, wagę i stan społeczno -ekonomiczny. Następnie informacje te są prezentowane w postaci tabel i wykresów.

Przykład 2

Aby monitorować lokalną drużynę piłkarską i dokonywać nowych podpisów, menedżerowie noszą liczbę rozegranych meczów, wygrali, remisowali i przegrały, a także liczbę bramek, strzelców i jak udało im się zdobyć: rzut wolny, z pół dworu, kar, karami, karami, karami, karami, karami, karami, karami z lewą nogą lub prawą, między innymi szczegółami.

Może ci służyć: wzajemnie wykluczające się wydarzenia: właściwości i przykłady

Przykład 3

Lce warsztat ma kilka smaków lodów i chce poprawić swoją sprzedaż, dlatego właściciele przeprowadzają badanie, w których liczą liczbę klientów, dzielą ich na grupy według płci i przedziału wiekowego.

Na przykład w tym badaniu w tym badaniu ulubiony smak lodów i najlepiej sprzedają się prezentacja. A ze zebranymi danymi planują zakupy smaków oraz niezbędne pojemniki i akcesoria do przygotowania.

Podstawowe pojęcia statystyki opisowej

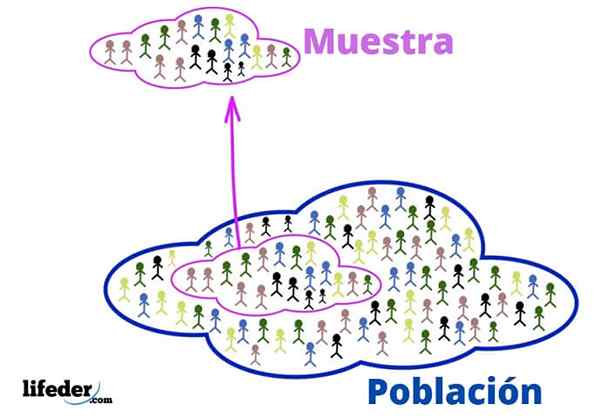Populacja i próbka

Te podstawowe pojęcia są niezbędne do zastosowania technik statystycznych, zobaczmy:

Populacja

W kontekście statystycznym populacja odnosi się do wszechświata lub kolektywu, od którego pochodzą informacje.

Nie zawsze chodzi o ludzi, ponieważ mogą to być zestawy zwierząt, roślin lub przedmiotów, takich jak samochody, atomy, cząsteczki, a nawet wydarzenia i pomysły.

Próbka

Gdy populacja jest bardzo duża, z niej wyodrębniana jest reprezentatywna próbka i analizowana, bez utraty odpowiednich informacji.

Można go wybrać losowo lub zgodnie z pewnymi kryteriami ustalonymi wcześniej przez analityka. Zaletą jest to, że będąc podzbiorem populacji, jest znacznie łatwiejsza do opanowania.

Zmienny

Odnosi się do zestawu wartości, które mogą przyjąć pewną cechę populacji. Badanie może zawierać różne zmienne, takie jak wiek, płeć, waga, poziom akademicki, status cywilny, dochód, temperatura, kolor, czas i wiele innych.

Zmienne mogą mieć inny charakter, więc istnieją kryteria ich klasyfikacji i zapewnienia im najbardziej odpowiedniego leczenia.

Zmienne kategoryczne i zmienne numeryczne

Zgodnie ze sposobem ich mierzonym zmienne mogą być:

-Kategoryczny

-Liczbowy

Zmienne kategoryczne, zwane również jakościowy, Reprezentują takie cechy, jak status cywilny osoby, która może być singlem, małżeństwem, rozwiedzioną lub wdową.

Z drugiej strony, do zmiennych numerycznych lub ilościowy, Można je zmierzyć, takie jak wiek, czas, waga, dochód i więcej.

Grafika jest bardzo ważna, aby przedstawić informacje, ponieważ na pierwszy rzut oka trend danych jest doceniany. Źródło: Piqsels.

Dyskretne i ciągłe zmienne zmienne

Zmienne dyskretne przyjmują tylko dyskretne wartości, jak sama nazwa. Przykładami są liczba dzieci rodziny, ile osób jest w określonym kursie i ilość samochodów na parkingu.

Te zmienne nie zawsze przyjmują całe wartości, ponieważ istnieją również ułamki.

Z drugiej strony zmienne ciągłe przyznają się do nieskończonych wartości w określonym zakresie, takich jak waga osoby, pH krwi, czas konsultacji telefonicznych i średnica piłek piłkarskich.

Może ci służyć: symetria

Miary tendencji centralnej

Daj wyobrażenie o ogólnym trendzie, który podąża dane. Wspomnimy o trzech najczęściej używanych środkach centralnych:

-Połowa

-Mediana

-Moda

Połowa

Równoważne średniej wartości. Jest to obliczane przez dodanie wszystkich obserwacji i dzieląc się między całkowitą liczbę:

 Gdzie x_Siema Jest to każda obserwacja, a n jest z nich suma.

Moda

Jest to wartość, która jest powtarzana najbardziej w zestawie danych, najczęstsza, ponieważ w dystrybucji może być więcej niż jedna moda.

Mediana

Przy zamawianiu zestawu danych mediana jest centralną wartością wszystkich z nich.

Miary dyspersji

Wskazują na zmienność danych i dają wyobrażenie o tym, jak daleko lub rozproszone są środki centralne. Najczęściej używane to:

Zakres

Jest to różnica między największą wartością x_M i najmniejszy x_M zbioru danych:

Zakres = x_M - X_M

Zmienność

Zmierz, jak daleko są dane o średniej wartości. W tym celu wykonana jest średnia, ale z różnicami między dowolną wartością x_Siema i średnia, kwadratowa, aby zapobiec ich anulowaniu. Zazwyczaj jest to oznaczone grecką literą σ kwadratową lub z s²:

Odchylenie standardowe

Wariancja nie ma takich samych jednostek jak dane, więc odchylenie standardowe jest zdefiniowane jako pierwiastek kwadratowy wariancji i jest oznaczony jako σ lub s:

Rozkłady częstotliwości

Zamiast brać pod uwagę każde dane indywidualnie, preferowane jest grupowanie ich w zakresie, co ułatwia pracę, szczególnie jeśli istnieje wiele wartości. Na przykład, pracując z dziećmi szkoły, można je pogrupować w zakresie wieku: od 0 do 6 lat, od 6 do 12 lat i od 12 do 18 lat.

Wykresy

Stanowią doskonały sposób na docenienie dystrybucji danych widoku i zawierają wszystkie informacje zebrane w tabelach i zdjęciach, ale znacznie bardziej przystępne cenowo.

Istnieje ich szeroka gama: z prętami, liniowymi, okrągłymi, łodygami i liśćmi, histogramami, wielokątami częstotliwości i piktogramami. Przykłady wykresów statystycznych przedstawiono na rycinie 3.

Interesujące tematy

Oddziały statystyczne.

Zmienne statystyczne.

Populacja i próbka.

Statystyka wnioskowania.

Bibliografia

1. Faraldo, s. 1. Statystyka i metodologia badań. Odzyskane z: EIO.USC.Jest.
2. Fernández, s. 2002. Opisowe statystyki. 2. Wydanie. ESIC EDYTORIAL. Odzyskane z: Google Books.
3. Historia statystyki. Odzyskane z: eumed.internet.
4. Ibañez, s. 2010. Matematyka II. Podejście kompetencyjne. Cengage Learning.
5. Monroy, s. 2008. Opisowe statystyki. 1st. Wydanie. National Polytechnic Institute of Mexico.
6. Formuły wszechświata. Opisowe statystyki. Odzyskane z: Universoformulas.com.