Helmholtz Free Energy jednostki, sposób obliczania, rozwiązanych ćwiczeń

Helmholtz Free Energy Jest to potencjał termodynamiczny, który mierzy użyteczną pracę systemu zamkniętego w stałej temperaturze i objętości. Bezpłatna energia Helmholtza jest oznaczona jako F I jest zdefiniowany jako różnica od energii wewnętrznej LUB mniej produktu temperaturowego T Dla entropii S:

F = u - tarcie

Ponieważ jest to energia, jest mierzona w dżuli w systemie międzynarodowym (SI), chociaż inne odpowiednie jednostki mogą być również ergios (CGS), kalorie lub wolty elektronowe (EV).

Rysunek 1. Definicja energii Helmholtza. Źródło: Pixabay.

Ujemna zmienność energii Helmholtza podczas procesu jest utożsamiana z maksymalną pracą, którą system może wykonywać w procesie izokorycznym, to znaczy do stałej objętości. Gdy objętość nie jest stała, część tej pracy można wykonać w środowisku.

W takim przypadku odnosimy się do pracy, w której objętość nie różni się, taka jak praca elektryczna: dw = φdq, z φ jako potencjał elektryczny i q jako ładunek elektryczny.

Jeśli temperatura jest również stała, energia Helmholtza jest zminimalizowana po osiągnięciu równowagi. Mimo to energia Helmholtza jest szczególnie przydatna w procesach o stałej objętości. W takim przypadku masz:

- Dla spontanicznego procesu: ΔF < 0

- Gdy układ jest w równowadze: ΔF = 0

- W procesie niestabilnym: ΔF> 0.

[TOC]

Jak obliczana jest Helmholtz Free Energy?

Jak stwierdzono na początku, energia Helmholtza jest definiowana jako „energia wewnętrzna lub system, z wyjątkiem iloczynu absolutnej temperatury systemu, przez entropię systemu”::

F = u - tarcie

Jest to funkcja temperatury t i objętości v. Kroki do wizualizacji są następujące:

Może ci służyć: wewnętrzne elektrony

- Począwszy od pierwszego prawa termodynamiki, energii wewnętrznej lub jest związane z entropią systemu i jego objętością V dla odwracalnych procesów poprzez następującą relację zróżnicowaną:

du = dq - dw = tds - PDV

Wynika to z tej energii wewnętrznej lub funkcji zmiennych S I V, W związku z tym:

U = u (s, v)

- Teraz definicja F I jest wyprowadzony:

df = du - d (ts) = du - tds - sdt

- Zastępowanie tam wyrażenia różnicowego uzyskane dla DU w pierwszym etapie pozostaje:

Df = TDS - PDV - TDS - SDT = -SDT - PDV

- Wreszcie stwierdzono, że F jest funkcją temperatury t i objętości V i można go wyrazić jako:

F = f (t, v)

Rysunek 2. Hermann von Helmholtz (1821–1894), niemiecki fizyk i lekarz, uznany za swój wkład w elektromagnetyzm i termodynamikę, między innymi obszarami nauki. Źródło: Wikimedia Commons.

Spontaniczne procesy

Energię Helmholtza można zastosować jako ogólne kryterium spontaniczności w izolowanych systemach, ale zanim należy określić pewne pojęcia:

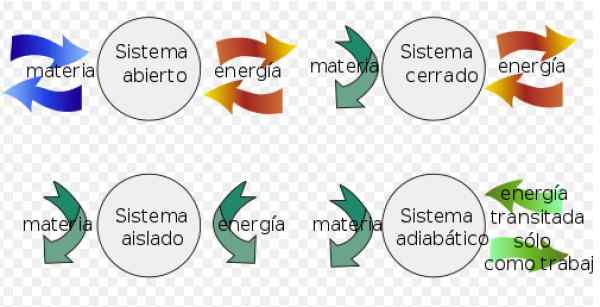
- A system zamknięty Może wymieniać energię z środowiskiem, ale nie może wymieniać materii.

- Zamiast tego system izolowany nie wymienia materii ani energii ze środowiskiem.

- Wreszcie a otwarty system wymieniać materię i energię ze środowiskiem. 

Rysunek 3. Systemy termodynamiczne. Źródło: Wikimedia Commons. Fjgar (bis) [cc by-sa (https: // creativeCommons.Org/licencje/nabrzeże/4.0)].

W procesach odwracalnych zmienność energii wewnętrznej jest obliczana w następujący sposób:

Du = TDS - PDV

Załóżmy teraz, że stały objętość (izokoryczna), w którym drugi termin poprzedniego wyrażenia ma zerowy wkład. Należy również pamiętać, że zgodnie z Nierówność Clausiusa: 

ds ≥ dq/t

Taka nierówność dotyczy izolowanego układu termodynamicznego.

Tak, że dla procesu (odwracalnego lub nie), w którym objętość jest utrzymywana stała, była spełniona:

Może ci służyć: kwas fosforowy (H3PO4)

T ds ≥ du (Przy stałej objętości)

Biorąc pod uwagę:

df = du - t ds 

Będziemy musieli w procesie izokorycznym w stałej temperaturze, jest spełnione, że: DF ≤ 0, Jak wskazano na początku.

Tak że energia Helmholtza F jest zmniejszającą ilością spontanicznego procesu, gdy jest to izolowany system. F osiąga swoją minimalną i stabilną wartość, gdy osiągnięto odwracalną równowagę.

Rozwiązane ćwiczenia

Ćwiczenie 1

Oblicz zmianę energii swobodnej Helmholtza F dla 2 moli idealnego gazu w temperaturze 300k podczas izotermicznej ekspansji, która prowadzi do układu początkowej objętości 20 litrów do końcowej objętości 40 litrów.

Rozwiązanie

Począwszy od definicji F:

F = u - t s

Wówczas skończona zmienność F, zwana ΔF, będzie:

ΔF = δu - t δs

Jak stwierdzenie stwierdza, że ​​temperatura jest stała: ΔT = 0. Jednak w gazach idealnych energia wewnętrzna zależy tylko od jej temperatury bezwzględnej, ale ponieważ jest to proces izotermiczny, zatem jest to proces izotermiczny Δu = 0 I ΔF = - t δs. W przypadku gazów idealnych, entropia odmiana procesu izotermicznego jest napisana w ten sposób: 

ΔS = n.R.LN (v₂/V₁)

Zastosowanie tego wyrażenia:

ΔS = 2 mole x 8314 J/(k mol) x ln (40l/20l) = 11,53 J/k

Wreszcie zmiana energii Helmholtza wynosi:

ΔF = - t δS = - 300K x 11,53 J/k = -3457,70 j.

Ćwiczenie 2

Wewnątrz cylindra znajduje się tłok, który dzieli go na dwie sekcje i po każdej stronie tłoka są N mole idealnego monoatomowego gazu, jak pokazano na poniższym rysunku.

Ściany cylindra są dobrymi przewodnikami cieplnymi (diatermiczny) i mają kontakt z zbiornikiem temperatury T_albo.

Początkowa objętość każdej z sekcji cylindrów to v_1i i v_2i, podczas gdy jego ostateczne tomy to V_1f i v_2f Po quasiestatycznym wysiedleniu. Tłok porusza się za pomocą tłoka, który hermetycznie przecina dwa cylindryczne tapas.

Może ci służyć: Tecnecio (TC): Struktura, właściwości, użycie, uzyskiwanie

Jest proszony o znalezienie:

a) Zmiana energii wewnętrznej gazu i pracy wykonanej przez system i

b) Zmiana energii Helmholtza.

Rozwiązanie

Gdy tłok porusza się quasstatycznie, siła zewnętrzna przyłożona do tłoka musi zrównoważyć siłę ze względu na różnicę ciśnienia w dwóch odcinkach cylindra.

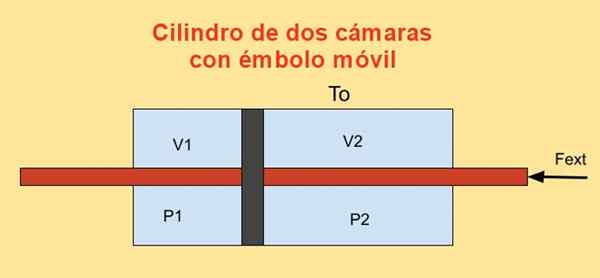Rysunek 4. Zmienność energii swobodnej f w cylindrze z dwoma kamerami. Źródło: f. Zapata.

Praca DW Wykonane przez siłę zewnętrzną F_ext Podczas nieskończenie małego przemieszczenia Dx Jest:

Dw = - f_ext Dx = (p₁ - P₂) A dx = p₁ DV₁ + P₂ DV₂

Gdzie stosowano związek DV₁ = - DV₂ = DX, istnienie Do Obszar tłokowy. Z drugiej strony zmienność energii Helmholtza wynosi: 

Df = -sdt - PDV

Ponieważ podczas procesu temperatura się nie zmienia, zatem DT = 0 I Df = - PDV. Zastosowanie tego wyrażenia do każdej sekcji cylindra, który masz:

dw = p₁ DV₁ + P₂ DV₂ = - df₁ - Df₂

Istnienie F₁  I F₂ Energie Helmholtza w każdej z kamer.

Skończone prace W można obliczyć na podstawie skończonej zmienności energii Helmholtza w każdej kamery:

W = -ΔF₁ - ΔF₂

Rozwiązanie b

Aby znaleźć zmianę energii z Helmholtza, używana jest definicja: F = u - t s. Jak w każdym kamerze masz idealny gaz monoatomowy w stałej temperaturze T_albo, Energia wewnętrzna nie zmienia się (δu = 0), więc: ΔF = - T_albo Δs. Oprócz:

ΔS = nr ln (v_F/Piła)

Że przez zastąpienie go w końcu pozwala na wykonaną pracę, to: 

W = -t_albo Nr ln (v_1f /V_1i) -To nr ln (v_2f /V_2i) = -ΔF₁ -ΔF₂

W = - do nr ln [(v_1f ⋅ v_1i)/(V_{2f .}V_2i)] = - δf_całkowity

Istnienie ΔF_całkowity Całkowita zmienność energii Helmholtza.

Bibliografia

1. Castaños e. Ćwiczenia energetyczne. Odzyskane z: lidiaconlachimica.WordPress.com
2. Librettexts. Helmholtz Energy. Odzyskane z: chem.Librettexts.org
3. Librettexts. Co to jest bezpłatna energia. Odzyskane z: chem.Librettexts.org
4. Wikipedia. Helmholtz Energy. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Helmholtz Free Energy. Źródło: w:.Wikipedia.com