Ogólne równanie paraboli (przykłady i ćwiczenia)

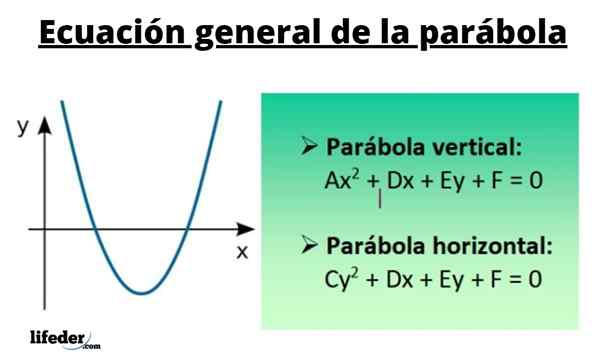
Równanie ogólne przypowieści zawiera kwadratowe warunki w X i w I, a także terminy liniowe w obu zmiennych plus niezależny termin. Pierwsza oś symetrii jest równoległa do osi pionowej, a druga to oś pozioma.

Zasadniczo równanie kwadratowe, które nie ma skrzyżowanego terminu Xy Jest napisane jako:

Topór² + Cy² +Dx + ey + f = 0

Wartości A, C, D, E i F są liczbami rzeczywistymi. Nałożenie warunków przy ∙ c = 0 i a+c ≠ 0, krzywa wynikająca z wykresu punktów, które spełniają to równanie, jest parabola.

Przypadek 1

Dla pionowej przypowieści jego ogólne równanie to:

Topór² + Dx + ey + f = 0

Gdzie A i E różnią się od 0. Innymi słowy, gdy pojawia się termin z x², Przypowieść jest pionowa.

Przypadek 2

Ze swojej strony, dla poziomej przypowieści: masz:

Cy² + Dx + ey + f = 0

Tutaj C i D różnią się również od 0, dlatego termin kwadratowy odpowiada i².

W każdym razie ogólne równanie przypowieści jest kwadratowe w jednej ze zmiennych, a liniowe w drugiej.

Elementy przypowieści

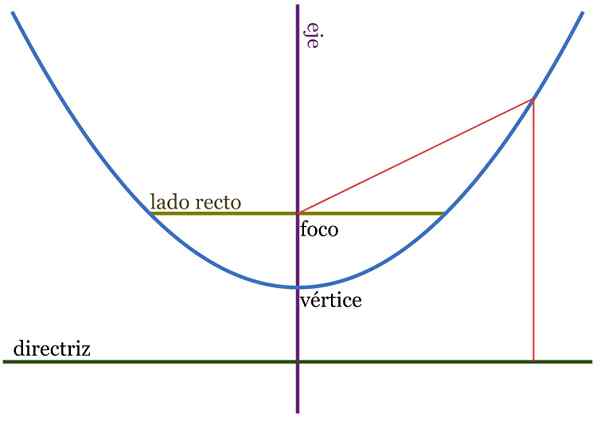Rysunek 2. Elementy przypowieści. Odległości QF i QH są równe. Źródło: Wikimedia Commons.

Parabola, zdefiniowana jako miejsce geometryczne, składa się z zestawu punktów jednej płaszczyzny, która równa się z innego punktu zwanego centrum A także linii, znanej jako proste wytyczne.

Z ogólnego równania możliwe jest zbadanie przypowieści, określając jej elementy. W tym skupienie i wytyczne, te elementy opisane krótko to:

-Oś, który odnosi się do osi symetrii paraboli, może być pozioma (równoległa do osi odciętej) lub pionowej (równolegle do osi rzędnych).

Może ci służyć: wspólny czynnik grupowania warunków: przykłady, ćwiczenia

-Orientacja, co z kolei odpowiada orientacji osi. Przypowieść jest pionowa, jeśli jej oś symetrii jest pionowa i jest pozioma, gdy osi jest również.

-Wierzchołek, Jest to punkt, w którym oś przecina się przypowieść.

-Centrum, punkt znajdujący się na osi, wewnątrz przypowieści i na odległość P wierzchołka. Wszystkie punkty paraboli równorzędnych skupiają się i kierunek wytycznych.

-Parametr, To jest odległość P Między skupieniem a wierzchołkiem.

-Proste wytyczne, który jest prostopadły do ​​osi y, a także odległości P wierzchołka przypowieści, ale jej nie przecina, ponieważ jest ona na zewnątrz.

-Prosta strona, To lina przechodzi przez skupienie, przecinając przypowieść w dwóch punktach, prostopadłe do jej osi.

-Ekscentryczność, że w przypadku paraboli zawsze jest warte 1.

-Reprezentacja graficzna.

Informacje o określeniu wszystkich tych elementów są zawarte w równaniu ogólnym.

Forma kanoniczna

Aby określić elementy paraboli, czasami wygodnie jest przekazać ogólną formę do kanonicznego kształtu tego samego, za pomocą metody wypełniania kwadratów w zmiennej kwadratowej.

Ta kanoniczna forma to:

(X-H)² = 4p (y-k)

Gdzie punkt (h, k) jest wierzchołkiem V przypowieści. Może również stać się kanoniczna forma ogólnego równania, opracowując znaczący produkt i przestawiając warunki.

Przykłady

Przykład 1

Poniżej ogólnie są równania paraboli:

a) 4x² + 5y - 3 = 0

b) 1 - 2y + 3x -i² = 0

W a) zidentyfikowane są współczynniki: a = 4, c = 0, d = 0, e = 5, f = -3. Jest przypowieścią, której oś symetrii jest pionowa.

Może ci służyć: podział syntetyczny

Ze swojej strony, w B) ogólne równanie pozostaje:

- I² + 3x - 2y + 1 = 0

A współczynniki to: c = -1, d = 3, e = -2 i f = 1.

Przykład 2

Następna przypowieść jest w formie kanonicznej:

(Y-1)² = 6 (X-3)

Aby znaleźć jego ogólne równanie, opracowywany jest godny godny produkt, a nawias przeprowadzany jest po prawej stronie:

I² -2y + 1 = 6x -18

Teraz wszystkie warunki po lewej są przekazywane i są dogrupowane wygodnie:

I² -2y + 1- 6x +18 = 0 → i² - 6x -2y + 19 = 0

Jak kwadratowy termin i² To jest pozioma przypowieść. Współczynniki to:

C = 1; D = -6; E = -2, f = 19.

Rozwiązane ćwiczenia

Ćwiczenie 1

Następna przypowieść jest ogólnie podana:

X² -10x -12Y - 11 = 0

Jest proszony o napisanie go w formie kanonicznej.

Rozwiązanie

Przejdź do formy kanonicznej jest osiągany poprzez wypełnienie kwadratów, w tym przypadku, w zmiennej x. Warunki w x zaczynają się w nawiasach:

(X² -10x) -12Y - 11 = 0

Musisz przekształcić to, co jest w nawiasach w idealny kwadratowy trynomial, który osiąga się przez dodanie 5², to oczywiście należy odjąć, ponieważ w przeciwnym razie wyrażenie jest zmienione. Pozostaje tak:

(X² −10x+5²) -12Y - 11–5²= 0

Trzy terminy w nawiasach stanowią idealny kwadratowy trynomial (X-5)². Można go sprawdzić, opracowując ten znaczący produkt do potwierdzenia. Teraz przypowieść pozostaje:

(X-5)² -12Y -36 = 0

Poniżej znajduje się uwzględnienie warunków poza nawiasem:

(X-5)² -12 (y +3) = 0

To w końcu przekształca się w:

(X-5)² = 12 (Y +3)

Przykład 2

Znajdź elementy poprzedniej przypowieści i zbuduj swoją grafikę.

Rozwiązanie

Wierzchołek

Wierzchołek paraboli ma współrzędne v (5, -3)

Może ci służyć: pryzmat wątrobowy

Oś

Linia x = 5.

Parametr

Jeśli chodzi o wartość parametru P który pojawia się w formie kanonicznej: (X-H)² = 4p (y-k) porównuje oba równania:

4p = 12

P = 12/4 = 3

Orientacja

Ta przypowieść jest pionowa i otwiera się. Ponieważ wierzchołek znajduje się przy x = 5, y = -3, wówczas osi symetrii jest linią pionową x = 5.

Centrum

Nacisk kładziony jest na wiersz x = 5, dlatego ma również współrzędną x = 5.

Współrzędna I Focus musi być jednostki P powyżej K, to znaczy: P + K = 3 + (-3) = 0, wówczas skupienie jest w punkcie (5.0).

Proste wytyczne

Jest prostopadle do osi, dlatego jest to forma y = c, teraz, ponieważ odległość p od wierzchołka jest daleka od, ale poza przypowieścią oznacza, że ​​znajduje się w odległości p poniżej k:

y = k -p = -3-3 = -6

Prosta strona

Ten segment przecina przypowieść, przechodzi przez skupienie i jest równolegle do wytycznych, dlatego jest zawarty w wierszu y = 0.

Reprezentacja graficzna

Można go łatwo uzyskać z bezpłatnego oprogramowania graficznego online, takiego jak Geogebra. W polu wejściowym jest umieszczony w następujący sposób:

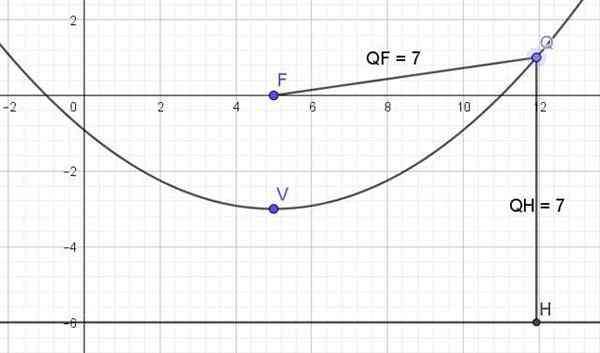Rysunek 3. Wykres przypowieści x² -10x -12Y - 11 = 0. Źródło: f. Zapata.

Bibliografia

1. Baldor. 1977. Algebra podstawowa. Wenezuelskie wydania kulturalne.
2. Hoffman, J. Wybór problemów z matematyką. Głośność 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.