Dynamika przykładów układu cząstek, ćwiczenia

Dynamika układu cząstek Składa się z zastosowania praw Newtona z ruchu do zestawu cząstek, które mogą być dyskretne (cząstki można policzyć) lub być częścią rozszerzonego obiektu, w tym przypadku układ jest ciągły.

Aby wyjaśnić ruch układu cząstek, analiza każdego z nich jest niewygodna. Zamiast tego zdefiniowany jest reprezentatywny punkt zestawu, zwany Mass Center.

Opisanie ruchu Mass Center oferuje bardzo udaną panoramę globalnego ruchu zestawu, pozwala również zastosować prawa Newtona analogiczne do tego, gdy obiekt jest uważany za cząstkę bez wymiarów.

Ten ostatni model, nazywany Model cząstek, Dobrze jest opisać tłumaczenia, a także gdy nie jest konieczne rozważanie wymiarów obiektu. Ale zwykłe obiekty mają rozmiar, a jeśli mają również ruch rotacyjny, należy wziąć pod uwagę punkty, w których stosowane są siły.

[TOC]

Przykłady

Ziemia i księżyc

Ilustracja Ziemi i Księżyca

Zestaw dyskretnych cząstek m₁, M₂, M₃... To ostatecznie porusza się w odniesieniu do pochodzenia układu współrzędnych, ze względu na pewną wynikową siłę, która na nich działa, jest dobrym przykładem układu cząstek.

Ziemi można uznać za jedną cząstkę, a Księżyc inna, wówczas oba stanowią układ 2 cząstek pod działaniem siły grawitacji Słońca.

Rozszerzone obiekty

Osoba, zwierzę lub dowolny obiekt środowiska, może być również uznane za układ cząstek, tylko że są one tak małe, że nie można policzyć jednego po drugim. Jest to system ciągły, ale biorąc pod uwagę pewne względy, jego leczenie jest takie samo jak w przypadku dyskretnego systemu.

Może ci służyć: jaki jest entalpia treningowa? (Z ćwiczeniami)

Oto szczegóły.

Masowe centrum układu cząstek

Aby rozpocząć badanie układu cząstek, musisz znaleźć centrum masy (cm), który jest punktem, w którym cała masa układu jest skoncentrowana.

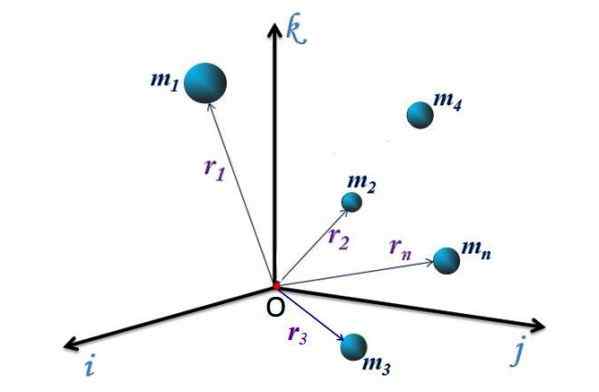
Rysunek 1. Układ cząstek w układzie referencyjnym XYZ. Źródło: f. Zapata.

Dla dyskretnego systemu z rysunku 1, z N cząstki, każda ma wektor położenia skierowany z układu pochodzenia lub współrzędnych do punktu p (x, y, z), gdzie jest cząstka. Wektory te są oznaczone jako R₁, R₂, R₃.. R_N.

Współrzędne CM są obliczane na podstawie następujących równań:

Gdzie każda masa zestawu jest reprezentowana jako m₁, M₂, M₃... M_N. Zauważ, że suma ∑ m_Siema Jest to równoważne z całkowitą masą M zestawu. Jeśli system jest ciągły, podsumowania są zastąpione całkami.

Każdy z prostopadłych adresów jest reprezentowany przez wektory jednostkowe Siema, J I k, Dlatego wektor położenia CM, oznaczony R_Cm, Można to wyrazić przez:

R_Cm = x_Cm Siema + I_Cm J + z_Cm k

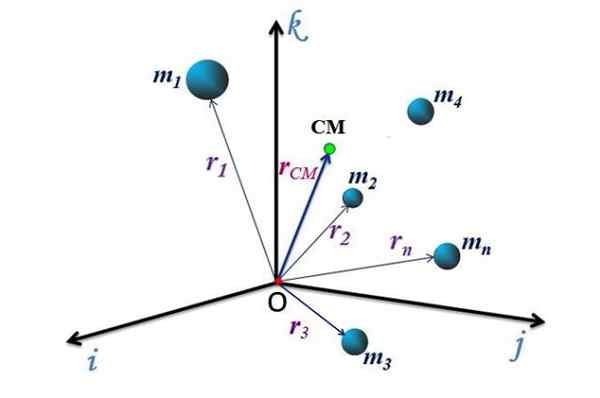Rysunek 2. Masowa lokalizacja układu cząstek. Źródło: f. Zapata.

Ruch CM

Po poznaniu lokalizacji centrum masowego stosowane są znane równania ruchu. Szybkość CM jest pierwsza pochodząca z pozycji w odniesieniu do czasu:

W takim przypadku system ma całkowity ruch P który jest obliczany jako iloczyn całkowitej masy systemu i prędkości centrum masy:

Może ci służyć: trajektoria fizyczna: cechy, typy, przykłady i ćwiczenia

P = M ∙v_Cm

Alternatywnie całkowita ilość systemu systemu można obliczyć bezpośrednio:

P = m₁v₁ + M₂v₂ + M₃v₃ +.. . = ∑ m_Siema v_Siema

Podczas gdy przyspieszenie CM jest uzyskane prędkość:

Siła na CM

Siły działające w systemie cząstek mogą być:

• Siły wewnętrzne, z powodu interakcji między tymi samymi cząsteczkami.
• Siły zewnętrzne, spowodowane przez agentów zewnętrznych w stosunku do systemu.

Ponieważ siły wewnętrzne są prezentowane przez pary o tej samej wielkości i kierunku, ale przeciwne zmysły, zgodnie z trzecim prawem Newtona, spełnione jest:

∑ F_int = 0

Dlatego siły wewnętrzne nie zmieniają ruchu całości, ale są one bardzo ważne, aby określić energię wewnętrzną.

Jeśli system jest odizolowany i nie ma sił zewnętrznych, zgodnie z pierwszym prawem Newtona, Mass Center jest w spoczynku lub porusza się z jednolitym ruchem prostoliniowym. W przeciwnym razie centrum masowych doświadczeń ma przyspieszenie podane przez:

∑ F_ext = M ∙Do_Cm

Gdzie m jest całkowitą masą systemu. Poprzednie równanie może być napisane w ten sposób:

I oznacza to, że siła zewnętrzna jest równoważna tymczasowej zmienności ilości ruchu, inny sposób wyrażania drugiego prawa Newtona i ten sam używany przez słynnego angielskiego fizyka w jego książce Zasada.

Ćwiczenie rozwiązane

Środek masy 2 układu cząstek znajduje się na osi x w pewnym momencie, w pozycji x = 2.0 mi poruszanie się z prędkością 5.0 m/s w tym samym kierunku i pozytywnie. Jeśli jedna z cząstek znajduje się na początku, a drugą, masy 0.1 kg, spoczywa na x = 8.0 m, oblicz:

Może ci służyć: diamagnetyzm: materiały, aplikacje, przykłady

a) Masa cząstki, która jest u źródła.

b) Ilość ruchu systemowego

c) jaka prędkość jest cząsteczką, która jest u źródła?

Rozwiązanie

Z równania pozycji Mass Center:

R_Cm = x_Cm Siema + I_Cm J + z_Cm K = 2.0 m Siema

Ponieważ CM ma tylko współrzędną X, zastosowano pierwsze wcześniej podane równanie trio:

Współrzędne są teraz zastępowane, jeśli cząstka jest oznaczona na początku, takie jak numer 1 i drugi, taki jak numer 2, dane numeryczne to:

X₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Cm = 2.0 m

Przebywający:

= 0.3 kg

Rozwiązanie b

Ilość ruchu systemowego jest obliczana przez:

P = M ∙v_Cm

Całkowita masa M jest równa:

M = 0.3 kg + 0.1 kg = 0.4 kg

Dlatego:

P = 0.4 kg ∙ 5.0 m/s Siema = 2 kg.SM Siema

Rozwiązanie c

Równania P z systemu dwupartyjnego, oczyszcza v₁, Ponieważ inne dane są znane, ponieważ stwierdzenie mówi, że cząstka 2 jest zatem w spoczynku:

v₂ = 0 

I P To po prostu jak:

P = m₁v₁

v₁ = P / M₁ = 2 kg.SM Siema / 0.3 kg = 6.67 m/s Siema

Bibliografia

1. Uniwersytet Duke. Układy cząstek. Odzyskane z: Webhome.Phy.Książę.Edu.
2. Rex, a. 2011. Podstawy fizyki. osoba.
3. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. osoba.
4. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.
5. Tipler, str. (2006) Physics for Science and Technology. Ed. Tom 1. Redakcja Reverted.