Symbole i formuły średnicy, jak to wyjąć, obwód

On średnica Jest to linia prosta, która przechodzi przez środek zamkniętej płaskiej krzywej lub figurę w dwóch lub trzech wymiarach, a także łączy się z jego przeciwnymi punktami. Zazwyczaj jest to okrąg (płaska krzywa), okrąg (płaska figura), kula lub prosty cylinder okrągły (trzy -wymiarowe obiekty).

Chociaż obwód i okrąg są zwykle traktowane jako synonimy, istnieje różnica między obiema terminami. Obwód jest zamkniętą krzywą otaczającą koło, który spełnia warunek, że odległość między dowolnym punktem a środkiem jest taka sama. Ta odległość jest niczym innym jak promieniem obwodu. Zamiast tego koło jest płaską postacią ograniczoną przez obwód.

Rysunek 1. Średnica kół rowerowych jest ważną cechą w projektowaniu. Źródło: Pixabay.

W przypadku obwodu, okręgu i kuli średnica jest segmentem prostym, który zawiera co najmniej trzy punkty: środek plus dwa punkty krawędzi obwodu lub okręgu lub powierzchnia kuli.

A co do prostego cylindra okrągłego, średnica odnosi się do przekroju, który wraz z wysokością są jej dwoma charakterystycznymi parametrami.

Średnica obwodu i okręgu, symbolizowany przez Ø lub po prostu literę „D” lub „D”, jest związana z jego obwodem, konturem lub długością, co jest oznaczone literą L:

L = π.D = π. albo

Ilekroć masz obwód, iloraz między jego długością a średnicą jest liczba irracjonalna π = 3.14159 ... w ten sposób:

π = l/d

[TOC]

Jak uzyskać średnicę?

Gdy rysunek obwodu lub okręgu jest dostępny lub bezpośrednio okrągły obiekt, taki jak na przykład waluta lub pierścień, bardzo łatwo jest przyjąć średnicę z regułą. Musisz po prostu upewnić się, że krawędź reguły w tym samym czasie ma dwa punkty obwodu i środek tego samego.

Może ci służyć: algebraiczna

Kaliber, nornie lub stopa króla jest bardzo odpowiednia do pomiaru zewnętrznych i wewnętrznych średnic w monetach, obręczach, pierścieniach, orzechach, rurkach i innych.

Rysunek 2. Nernier Digital mierząc średnicę monety. Źródło: Pixabay.

Jeśli zamiast obiektu lub jego rysunku masz dane takie jak radio R, Następnie pomnożenie przez 2 masz średnicę. A jeśli znana jest długość lub obwód obwodu, średnica może być również znana przez prześwit:

D = 2.R
D = l / π

Innym sposobem na uzyskanie średnicy jest poznanie obszaru okręgu, sferycznej powierzchni, przekroju cylindra, zakrzywionego obszaru tego lub objętości kuli lub cylindra. Wszystko zależy od tego, która figura geometryczna jest to. Na przykład średnica jest zaangażowana w następujące obszary i objętości:

-Obszar okręgu: π.(D/2)²
-Sferyczna powierzchnia: 4π.(D/2)²
-Objętość kuli: (4/3) π.(D/2)³
-Prosta okrągła objętość cylindra: π.(D/2)².H (H to wysokość cylindra)

Figury o stałym szerokim

Okrąg jest płaską postacią o stałej szerokości, ponieważ gdziekolwiek wygląda, szerokość wynosi średnicę d. Istnieją jednak inne, być może mniej znane postacie, których szerokość jest również stała.

Najpierw zobaczmy, co rozumiane jest przez szerokość figury: jest to odległość między dwiema równoległymi liniami -Support Remes -które z kolei są prostopadłe do danego kierunku i uwięziono figurę, jak pokazano na lewym obrazie:

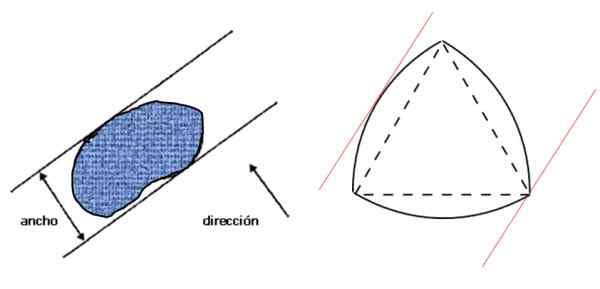Rysunek 3. Szerokość dowolnego płaskiego rysunku (po lewej) i trójkąta Reuleaux, stała szeroka figura (po prawej). Źródło: f. Zapata.

Następnie po prawej jest trójkąt Reuleaux, który jest stałą szeroką liczbą i spełnia warunki określone na lewej figurze. Jeśli szerokość postaci wynosi D, jej obwód jest podany przez twierdzenie Barbiera:

Może ci służyć: przybliżony pomiar liczb amorficznych: przykład i ćwiczenie

L = π.D

Kanały miasta San Francisco w Kalifornii mają kształt trójkąta Reuleaux, nazwany przez niemieckiego inżyniera Franza Reuleaux (1829 - 1905). W ten sposób tapas nie może spaść z otworu i wydać mniej materiału, aby je wyprodukować, ponieważ ich obszar jest mniejszy niż w kręgu:

A = (1- √3).πd² = 0.705.D²

Podczas gdy dla koła:

A = π.(D/2)² = (π/4) d²= 0.785.D²

Ale ten trójkąt nie jest jedyną stałą szeroką liczbą. Połączenia można zbudować Wielokąty Reuleaux z innymi wielokątami, które mają dziwną liczbę.

Średnica obwodu

Na następnym rysunku znajdują się elementy obwodu, zdefiniowane w następujący sposób:

Lina: segment linii, który łączy dwa punkty obwodu. Na rysunku jest lina, która łączy punkty C i D, ale nieskończone struny można prześledzić, że wyjątkowa każda para punktów obwodu.

Średnica: To lina przechodzi przez centrum, łącząc dwa punkty obwodu z centrum lub. Jest to najdłuższa lina obwodu, z tego powodu nazywa się go „główną liną”.

Radio: segment linii, który dołącza do centrum z dowolnym punktem obwodu. Jego wartość, podobnie jak średnica, jest stała.

Obwód: To zestaw wszystkich punktów, które zrównują lub.

Ukłon: Jest zdefiniowany jako segment obwodu ograniczony przez dwa radiotelefony (nie narysowane na rysunku).

Rysunek 4. Części obwodu, w tym średnica, która przechodzi przez centrum. Źródło: Wikimedia Commons.

- Przykład 1

Pokazany prostokąt mierzy 10 cali wysokości, który podczas kręcenia tworzy prosty okrągły cylinder, którego średnica wynosi 5 cali. Odpowiedz na następujące pytania:

Może ci służyć: wzajemnie wykluczające się wydarzenia: właściwości i przykłady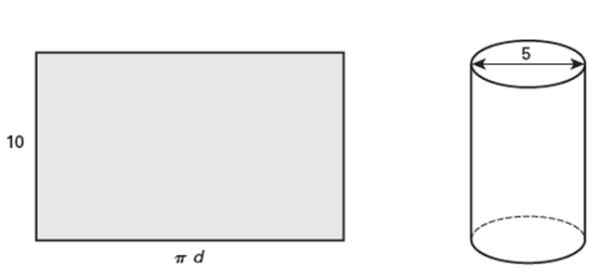Rysunek 5. ROZWIĄZANY ROZMIAR staje się prostym okrągłym cylindrem. Źródło: Jiménez, r. Matematyka II. Geometria i trygonometria. 2. Wydanie. osoba.

a) Jaki jest kontur rurki?
b) Znajdź obszar prostokąta
c) Oblicz powierzchnię krzyżową cylindra.

Rozwiązanie

Kontur rurki wynosi l = π.D = 5π PLG = 15.71 Plg.

Rozwiązanie b

Obszar prostokąta jest Podstawa X Wysokość, Będąc podstawą L już obliczoną, a wysokość wynosi 10 PLG zgodnie z stwierdzeniem, zatem:

A = 15.71 PLG x 10 PLG = 157.1 plg².

Rozwiązanie c

Wreszcie, żądany obszar jest obliczany w następujący sposób:

A = π.(D/2)² = (π/4) d² = (π/4) x (5 PLG)²= 19.63 Plg².

- Przykład 2

Oblicz zacieniony obszar na rycinie 5a. Kwadrat ma stronę l.

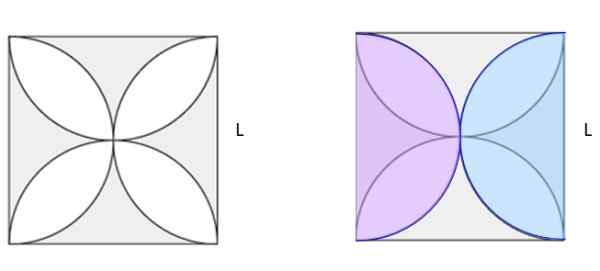Rysunek 6. Znajdź zacieniony obszar na lewej figurze. Jiménez, r. Matematyka II. Geometria i trygonometria. 2. Wydanie. osoba.

Rozwiązanie

Na rycinie 5b narysowano dwa identyczne półkole wielkości w różowych i niebieskich kolorach, nałożone na oryginalną figurę. Między nimi tworzą pełne koło. Jeśli obliczany jest kwadrat kwadratu, a obszar okręgu odejmuje, sprawia, że ​​zacieniony obszar na rycinie 5b. I wygląda dobrze, okazuje się, że jest to połowa zacienionego obszaru w 5A.

-Obszar: L²
-Średnica półkola: L
-Obszar okręgu: π.(L/2)²= (π/4) l²
-Różnica obszarów = połowa zacienionego obszaru =

L² - (π/4) L² = [(4 - π)/4] l²= 0.2146 L²

-Zacieniony obszar = 2 x 0.2146 L²= 0.4292L2

Ile średnich ma obwód?

Nieskończone średnice można narysować w okręgu, a każdy z nich mierzy to samo.

Bibliografia

1. Antonio. Reuleaux Trójkąty i inne krzywe o stałej szerokości. Odzyskane z: rozpowszechnianie.com.
2. Baldor, a. 2002. Płaska, przestrzeń i geometria trygonometrii. Grupa kulturowej ojczyzny.
3. Jiménez, r. Matematyka II. Geometria i trygonometria. 2. Wydanie. osoba.
4. Wikipedia. Trójkąt Reuleaux. Odzyskane: to jest.Wikipedia.org.
5. Wolfram Mathworld. Średnica. Odzyskane z: Mathworld.Wolfram.com.