Moody Schemat Równania, do czego służy,

On Moody Schemat Składa się z serii krzywych narysowanych na papierze logarytmicznym, które są używane do obliczenia współczynnika tarcia obecnego w przepływie turbulentnego płynu przez okrągły kanał.

Z współczynnikiem tarcia F Oceniana jest utrata energii tarcia, ważna wartość do określenia właściwej wydajności pomp, które rozkładają płyny, takie jak woda, benzyna, ropa.

Rury na poziomie przemysłowym. Źródło: Pixabay.

Poznać energię w przepływie płynu, jest to konieczne, a ściany rury.

[TOC]

Równania energii płynu ruchowego

Między dwoma odcinkami rury, oznaczonych jako 1 I 2, Możliwe jest ustalenie następującej równowagi, która jest rozszerzeniem równania Bernoulli: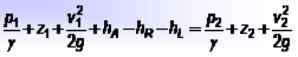Gdzie:

- P₁ I P₂ to ciśnienia w każdym punkcie,

- z₁ I z₂ są wysokościami w odniesieniu do punktu odniesienia,

- v₁ I v₂ są odpowiednie prędkości płynu,

- H_DO Jest to energia dodana przez pompy, H_R Jest to energia pobrana przez urządzenie takie jak silnik i H_L Obejmuje straty energii płynu z powodu tarcia między tym a ścianami rur, a także innych drobnych strat.

Wartość H_L Oblicza się go za pomocą równania Darcy-Weisbach:

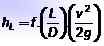
Gdzie L Jest to długość rury, D Jest to jej wewnętrzna średnica, v Jest to prędkość płynu i G Jest to wartość przyspieszenia grawitacji. Wymiary H_L Są długie i zwykle jednostki, w których jest reprezentowane, to metry lub stopy.

-Współczynnik tarcia i liczba Reynoldsa

Liczyć F Można zastosować równania empiryczne uzyskane z danych eksperymentalnych. Konieczne jest rozróżnienie, czy jest to płyn w reżimie laminarnym, czy turbulentnym. Dla reżimu laminarnego F Można go łatwo ocenić:

F = 64/n_R

Gdzie N_R Jest to liczba Reynoldsa, której wartość zależy od reżimu, w którym znajduje się płyn. Kryteria to:

Przepływ laminarny: N_R < 2000 el flujo es laminar; Flujo turbulento N_R > 4000; Reżim przejściowy: 2000 < N_R < 4000

Z kolei liczba Reynoldsa (bezwymiarowa) zależy od prędkości płynu v, Wewnętrzna średnica rurociągu D i lepkość kinematyczna N płynu, którego wartość jest uzyskiwana przez tabele:

Może ci służyć: równomiernie przyspieszony ruch prostoliniowy: Charakterystyka, formuły

N_R = v.D /N

Równanie Colebrook

W przypadku przepływu turbulentnego najbardziej akceptowanym równaniem w rur miedzianych i szklanych jest Cyryl Colebrook (1910–1997), ale ma to niedogodność F To nie jest wyraźne:

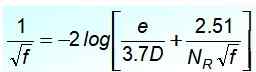
W tym równaniu iloraz E/D Jest to względna chropowatość rury i N_R To jest numer Reynoldsa. Podczas uważnego obserwowania zauważa się, że nie jest łatwo odejść F Po lewej stronie równości, więc nie jest to wygodne do natychmiastowych obliczeń.

Sam Colebrook zasugerował to podejście, które jest wyraźne, ważne z pewnymi ograniczeniami:

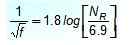
Po co to jest?

Schemat Moody'ego jest przydatny do znalezienia współczynnika tarcia F uwzględnione w równaniu Darcy, z uwagi na fakt, że w równaniu Colebrook nie jest łatwo wyrazić F bezpośrednio pod względem innych wartości.

Jego użycie upraszcza uzyskanie wartości F, zawierając graficzną reprezentację F w funkcji N_R Dla różnych wartości względnej chropowatości w skali logarytmicznej.

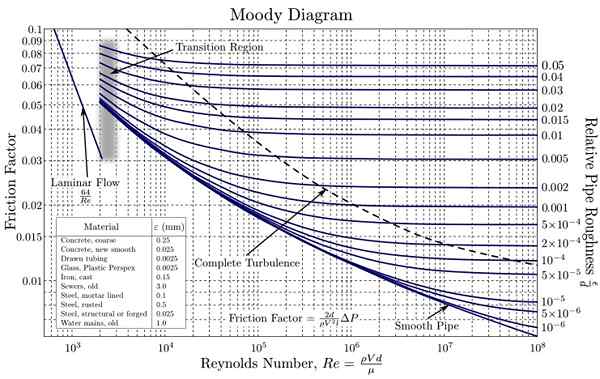Moody Schemat. Źródło: https: // prześlij.Wikimedia.org/wikipedia/commons/d/d9/Moody_en.Svg

Krzywe te zostały utworzone na podstawie danych eksperymentalnych z różnymi materiałami powszechnie stosowanymi w produkcji rur. Użycie skali logarytmicznej zarówno dla F Jeśli chodzi o N_R Jest to konieczne, ponieważ obejmują bardzo szeroki zakres wartości. W ten sposób ułatwia wykres wartości różnych rzędów wielkości.

Pierwszy wykres równania Colebrook uzyskał inżynier Hunter Rouse (1906–1996) i wkrótce potem zmodyfikował przez Lewisa F. Moody (1880–1953) w sposób, w jaki jest obecnie używany.

Jest stosowany zarówno do rur okrągłego, jak i nieczystego, wystarczy, aby wymienić dla nich średnicę hydrauliczną.

Jak to się robi i jak jest używane?

Jak wyjaśniono powyżej, diagram nastrojowy jest wykonany z wielu danych eksperymentalnych, przedstawiony graficznie. Oto kroki, aby go użyć:

- Oblicz numer Reynoldsa N_R Aby ustalić, czy przepływ jest laminarny czy turbulentny.

- Obliczyć względną chropowatość według równania I_R = E/D, Gdzie I Jest to absolutna chropowatość materiału, a D jest wewnętrzną średnicą rury. Wartości te są uzyskiwane przez tabele.

- Teraz, gdy jest dostępny I_R I N_R, projekt pionowo, aż do osiągnięcia krzywej odpowiadającej I_R uzyskany.

- Projekt w poziomie i po lewej stronie, aby odczytać wartość F.

Przykład z łatwością wizualizuje, w jaki sposób używany jest schemat.

Może ci służyć: fluor wapnia (CAF2): struktura, właściwości, zastosowania

-Rozwiązany przykład 1

Określ współczynnik tarcia wody w temperaturze 160º F z prędkością 22 stóp/s w kanale wykonanym z nieokreślonego żelaza z kutego i wewnętrznej średnicy 1 cala.

Rozwiązanie

Niezbędne dane (znajdują się w tabelach):

Lepkość kinematyczna wody w 160 ° F: 4.38 x 10^-6 stopa²/S

Absolutna chropowatość kutego żelaza, który nie jest pokryty: 1.5 x 10 ^-4 stopy

Pierwszy krok

Liczba Reynoldsa jest obliczana, ale nie przed przekazaniem wewnętrznej średnicy 1 cala na stopy:

1 cal = 0.0833 stóp

N_R = (22 x 0.0833)/ 4.38 x 10^-6= 4.18 x 10 ⁵

Zgodnie z kryteriami pokazanymi przed tym, jak jest to przepływ turbulentny, wówczas schemat Moody umożliwia uzyskanie odpowiedniego współczynnika tarcia, bez konieczności korzystania z równania Colleebrook.

Drugi krok

Musisz znaleźć względną szorstkość:

I_R = 1.5 x 10 -4 / 0.0833 = 0.0018

Trzeci krok

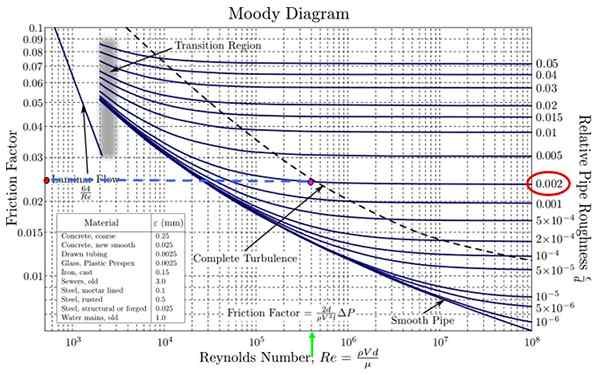
Na dostarczonym schemacie Moody'ego jest konieczne. Nie ma żadnego, który odpowiada dokładnie o 0.0018, ale jest taki, który dużo się zbliża, 0.002 (czerwony owal z rysunku).

Jednocześnie odpowiednia liczba Reynoldsa jest poszukiwana na osi poziomej. Wartość najbardziej podobna do 4.18 x 10 ⁵ jest 4 x 10 ⁵ (Zielona strzałka na rysunku). Przecięcie obu jest punktem Fuchsia.

Czwarty krok

Projekt lewej po lewej kropkowanej linii i przejdź do pomarańczowego punktu. Teraz oszacuj wartość F, Biorąc pod uwagę, że podziały nie mają takiego samego rozmiaru, jak w skali logarytmicznej zarówno w osi poziomej, jak i pionowej.

Moody schemat dostarczony na rysunku nie ma drobnych podziałów poziomych, więc wartość F w 0.024 (jest między 0.02 i 0.03 Ale to nie jest połowa, ale trochę mniej).

Istnieją kalkulatory online, które korzystają z równania Colleebrook. Jeden z nich (patrz odniesienia) dostarczona wartość 0.023664639 dla współczynnika tarcia.

Aplikacje

Moody Schemat można zastosować w celu rozwiązania trzech rodzajów problemów, pod warunkiem, że znany są płyn i absolutna chropowatość rury:

- Obliczanie spadku ciśnienia lub różnicy ciśnienia między dwoma punktami, dostarczane długość rury, różnica wysokości między dwoma punktami, którą należy wziąć pod uwagę, prędkość i wewnętrzną średnicę rury.

Może ci służyć: ruch wahadłowy

- Określenie przepływu, znanego długości i średnicy rury, plus specyficzny spadek ciśnienia.

- Ocena średnicy rury, gdy znana jest długość, przepływ i spadek ciśnienia między punktami, które są znane.

Problemy pierwszego typu są rozwiązywane bezpośrednio za pomocą schematu, podczas gdy problemy drugiego i trzeciego typu wymagają użycia pakietu obliczeniowego. Na przykład w trzecim typie, jeśli średnica rury nie jest znana, liczby Reynoldsa nie może być oceniana bezpośrednio, ani względnej chropowatości.

Jednym ze sposobów ich rozwiązania jest przejęcie początkowej średnicy wewnętrznej i stamtąd sukcesywnie dostosowanie wartości, aby uzyskać spadek ciśnienia określony w problemie.

-Rozwiązany przykład 2

Ma wodę w temperaturze 160 ° F zaparkowaną wzdłuż 1 -calowej rury w kutej średnicy żelaza. Określ różnicę ciśnienia spowodowaną tarciem i mocą pompowania niezbędną do utrzymania przepływu w odcinku poziomej rury o długości L = 200 stóp.

Rozwiązanie

Niezbędne dane: przyspieszenie grawitacji wynosi 32 stóp/s² ; Specyficzna waga wody w 160 ° F wynosi γ = 61.0 lb force/stopa³

Jest to rura przykładu rozwiązanego 1, dlatego współczynnik tarcia jest już znany F, który został oszacowany na 0.0024. Ta wartość jest przeniesiona do równania Darcy w celu oceny strat tarcia:

Niezbędna moc pompowania to:

W = v. DO. (P₁ - P₂)

Gdzie A jest przekrojem rurki: a = p. (D²/4) = P. (0.0833²/4) stopa² = 0.00545 stóp²

W = 22 stóp /s . 2659.6 funtów force / stopa². 0.00545 stóp²= 318.9 funtów . stopy

Moc jest lepiej wyrażona w Watts, dla których wymagany jest współczynnik konwersji:

1 wat = 0.737 LB Force . stopy

Dlatego moc wymagana do utrzymania przepływu wynosi w = 432.7 w

Bibliografia

1. Cimbala, c. 2006. Mechanika płynów, podstaw i zastosowań. MC. Graw Hill. 335-342.
2. Franzini, J. 1999. Mechanika płynów z zastosowaniem jest w inżynierii. MC. Graw Hill.176-177.
3. LMNO Engineering. Współczynnik kalkulatora tarcia Moody'ego. Odzyskane z: lmnoeng.com.
4. Mott, r.  2006. Mechanika płynów. 4. Wydanie. Edukacja Pearsona. 240-242.
5. Zestaw narzędzi inżynierii. Moody Schemat. Odzyskane z: EngineeringToolbox.com
6. Wikipedia. Moody wykres. Odzyskane z: w.Wikipedia.org