Przewodnictwo elektryczne i przykłady gęstości prądu

Nazywa się gęstość prądu do ilości prądu na jednostkę obszaru przez kierowcę. Jest to wielkość wektora, a jego moduł jest podany przez iloraz między prądem natychmiastowym i który przecina przekrój kierowcy i obszar S tego samego, aby:

Kierunek wektora gęstości prądu jest kierunkiem wektora jednostki normalnej do przekroju n, a wreszcie kierunek jest taki sam jak prąd, który według konwencji jest traktowany jako ten, który miałby dodatni nośnik obciążenia.

W ten sposób jednostki w systemie międzynarodowym dla wektora prądu gęstości to wzmacniacze na metr kwadratowy: A/M². Wektorowo gęstość prądu wynosi:

Na poniższym rysunku wektorem gęstości prądu, którego wielkość jest w tym przypadku J (y, z), to znaczy funkcja współrzędna J, I, I z. S to powierzchnia krzyżowa, która jest ilustrowana kwadrat, ale może mieć dowolną inną formę, zwykle jest okrągły.

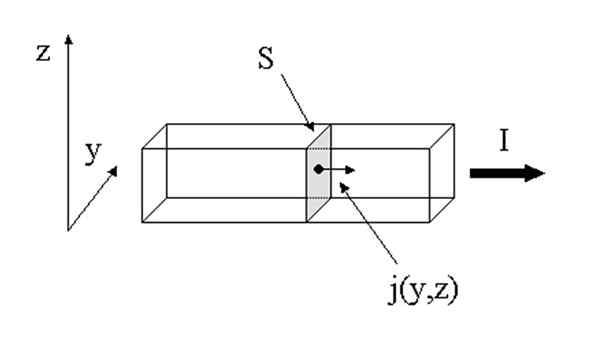Wektor prądu gęstości. Źródło: Wikimedia Commons.

Gęstość prądu i intensywność prądu są powiązane, chociaż pierwszy to wektor, a drugi nie jest. Prąd nie jest wektorem pomimo wielkości i znaczenia, ponieważ posiadanie preferencyjnego kierunku w przestrzeni nie jest konieczne do ustalenia koncepcji.

Jednak pole elektryczne ustanowione wewnątrz kierowcy jest wektorem i jest związane z prądem. Intuicyjnie rozumie się, że pole jest bardziej intensywne, gdy prąd jest również bardziej intensywny, ale przekrój kierowcy odgrywa również decydującą rolę w tym aspekcie.

[TOC]

Model jazdy elektrycznej

W kawałku neutralnego przewodu przewodzącego, takiego jak ten pokazany na rycinie 3, w cylindryczny sposób, nośniki obciążenia poruszają się losowo w dowolnym kierunku. W ramach kierowcy, zgodnie z rodzajem substancji, którą jest wykonany, będzie N Nośnik obciążenia na jednostkę objętości. Nie należy mylić z normalnym wektorem prostopadłym do powierzchni przewodzącej.

Kawałek cylindrycznego przewodu pokazuje wewnątrz bieżących nośników, którzy poruszają się w różnych kierunkach. Źródło: Self Made.

Proponowany model materiału postępowania składa się ze stałej sieci jonowej i gazu elektronowego, które są obecnymi przewoźnikami, nawet jeśli są tutaj reprezentowane ze znakiem +, ponieważ jest to konwencja dla bieżącego.

Co się stanie, gdy sterownik łączy się z baterią?

Wówczas ustalono potencjalną różnicę między końcami kierowcy, dzięki źródłem odpowiedzialnym za wykonanie pracy: bateria.

Może ci służyć: ciała niebieskie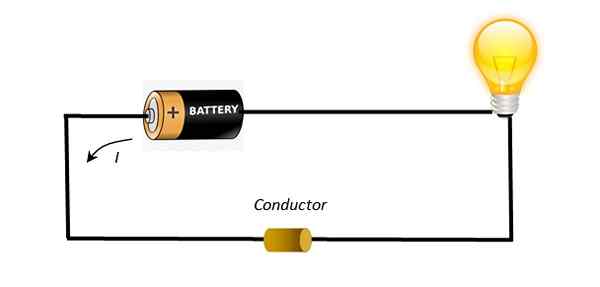Prosty obwód pokazuje akumulator, który według przewodów sterownika obraca się żarówkę. Źródło: Self Made.

Dzięki tej potencjalnej różnicy obecni przewoźnicy przyspieszają i maszerują w bardziej uporządkowany sposób niż wtedy, gdy materiał był neutralny. W ten sposób możesz zapalić żarówkę pokazanego obwodu.

W takim przypadku w sterowniku utworzono pole elektryczne, które przyspiesza do elektronów. Oczywiście ich ścieżka nie jest bezpłatna: chociaż elektrony mają przyspieszenie, ponieważ zderzają się z siecią krystaliczną, rezygnują z części energii i rozpraszają się cały czas. Globalny wynik polega na tym, że poruszają się nieco bardziej w materiale, ale z pewnością ich postęp jest bardzo niewielki.

Kiedy zderzają się z krystaliczną siecią, powodują, że wibruje, co powoduje ogrzewanie kierowcy. Jest to efekt, który można łatwo zauważyć: kable przewodzące są ogrzewane, gdy są skrzyżowane przez prąd elektryczny.

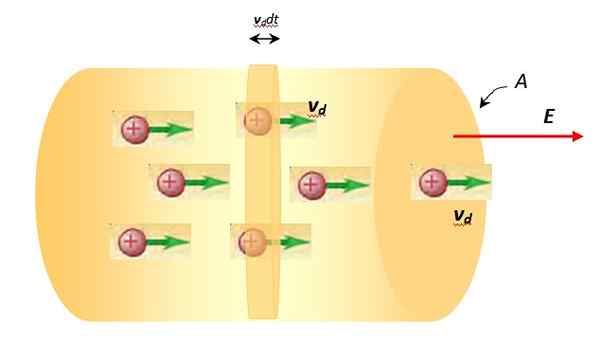
Prędkość oporu v_D  i gęstość prądu

Obecni nosiciele mają teraz globalny ruch w tym samym kierunku, co pole elektryczne. Ta globalna prędkość, którą mają, nazywa się prędkość przeciągania albo prędkość dryfu I jest symbolizowany jako v_D.

Po ustaleniu potencjalnej różnicy obecni przewoźnicy mają bardziej uporządkowany ruch. Źródło: Self Made.

Można go obliczyć na podstawie niektórych prostych rozważań: odległość przebywająca wewnątrz sterownika dla każdej cząstki, w przedziale czasowym Dt Jest v_D . Dt. Jak powiedziano wcześniej, są N Cząstki na jednostkę objętości, przy czym objętość jest iloczynem obszaru przekroju A według przebywanej odległości:

V = a.v_D Dt

Jeśli każda cząstka ma obciążenie q, ile obciążenia DQ przechodzi przez obszar DO W przedziale czasowym Dt?:

dq = q.N. DO.v_D Dt

 

Natychmiastowy prąd to tylko DQ/DT, dlatego:

A podzielenie między a jest uzyskiwane przez wektor gęstości prądu j:

J = q.N.v_D

Kiedy obciążenie jest dodatnie, v_D jest w tym samym kierunku co I  I J. Jeśli obciążenie było ujemne, v_D  jest przeciwny do pola I, Ale J I I Nadal mają ten sam adres. Z drugiej strony, nawet jeśli prąd jest taki sam w całym obwodzie, gęstość prądu niekoniecznie pozostaje niezmieniona. Na przykład jest niższy w baterii, której powierzchnia przekroju jest większa niż w przewodach napędowych, cieńsza.

Przewodność materiału

Można pomyśleć, że nośnicy obciążeni poruszają się do kierowcy i ciągle zderzają się z siecią krystaliczną, stają w obliczu siły, która sprzeciwia się ich postępowi, rodzajem tarcia lub siły rozpraszającej F_D co jest proporcjonalne do średniej prędkości, jaką noszą, to znaczy prędkość oporu:

Może ci służyć: zalety i wady tarcia

F_D ∝ v

F_D = α. v_D

To jest model Drude-Lorentz, stworzony na początku XX wieku w celu wyjaśnienia ruchu obecnych przewoźników wewnątrz kierowcy. Nie bierze pod uwagę efektów kwantowych. α jest stałą proporcjonalności, której wartość jest zgodnie z charakterystyką materiału.

Jeśli prędkość oporu jest stała, suma sił działających na nosicielu obecnym wynosi zero. Drugą siłą jest ta wykonywana przez pole elektryczne, którego wielkość jest Fe = q.I:

QE - α. v_D = 0

Prędkość oporu można wyrazić w kategoriach gęstości prądu, jeśli jest wygodnie wyczyszczona:

Dlatego:

Skąd:

J = nq²E/α

Stałe n, q i α są pogrupowane w pojedyncze wezwanie σ, aby ostatecznie zostało ono uzyskane:

 J = σI

Prawo Ohma

Gęstość prądu jest wprost proporcjonalna do pola elektrycznego ustalonego wewnątrz kierowcy. W tym wyniku jest to znane jako Prawo Ohma w formie mikroskopowej lub lokalnym prawu OHM.

Wartość σ = n.Q² / α jest stałą, która zależy od materiału. Chodzi o Przewodność elektryczna lub po prostu przewodność. Jego wartości są tabelowane dla wielu materiałów, a ich jednostki w systemie międzynarodowym to miernik AMP/Volt X (A/V.m), chociaż istnieją inne jednostki, na przykład S/M (Siemens na metr).

Nie wszystkie materiały są zgodne z tym prawem. Ci, którzy to robią, są znani jako Materiały omowe.

W substancji o wysokiej przewodności łatwo jest ustanowić pole elektryczne, podczas gdy w innym o niskiej przewodności kosztuje więcej pracy. Przykładami materiałów o wysokiej przewodności to: grafen, srebro, miedź i złoto.

Przykłady aplikacji

-Rozwiązany przykład 1

Znajdź prędkość oporu darmowych elektronów w miedzianym kablu przekroju 2 mm² Kiedy przechodzi przez niego prąd 3. Miedź ma 1 elektron napędowy na atom.

Fakt: Numer Avogadro = 6 023 10²³ cząsteczki Mol; Obciążenie elektronowe -1.6 x 10^-19 C; Gęstość miedzi 8960 kg/m³; Materia cząsteczkowa miedzi: 63,55 g/mol.

Rozwiązanie

Z J = q.N.v_D Wielkość prędkości oporu jest oczyszczona:

Aby ułatwić obliczenia, wartość N, która jest liczbą nośników obciążenia na jednostkę objętości, wówczas określana jest wielkość J i wreszcie wszystko jest zastąpione w poprzednim wyrażeniu:

Może ci służyć: zmienna kategorialna: cechy i przykłady

Jak natychmiast pojawiają się światła?

Ta prędkość jest zaskakująco. Na przykład może zająć elektron przez prawie godzinę od akumulatora samochodowego do żarówki latarni morskiej.

Na szczęście nie musisz tak długo czekać, aby zapalić światła. Elektron na baterii szybko popycha innych do kierowcy, a zatem pole elektryczne jest ustalane bardzo szybko, ponieważ jest fali elektromagnetycznej. Jest to zakłócenia, które rozprzestrzeniają się w drucie.

Elektrronom udaje się skakać z prędkością światła atomu do sąsiedniego, a prąd zaczyna płynąć w taki sam sposób, jak woda robi to przez wąż. Krople na początku węża nie są takie same jak na wyjściu, ale jest to również woda.

-Rozwiązany przykład 2

Rysunek pokazuje dwa połączone przewody wykonane z tego samego materiału. Prąd, który wchodzi z lewej do cieńszej części, wynosi 2 do. Tam prędkość oporu elektronów 8.2 x 10^-4 SM. Zakładając, że wartość prądu pozostaje stała, znajdując prędkość oporu elektronów w części prawej, w M/S.

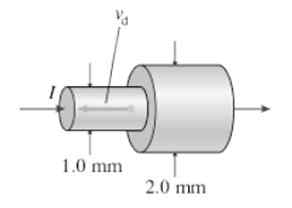
Rozwiązanie

W rozdziale cieńszym: j₁ = n.Q. v_D1 = I/A₁

I w najgrubszym odcinku: j₂ = n.Q. v_D2 = I/A₂

Prąd jest taki sam dla obu sekcji, a także N I Q, W związku z tym:

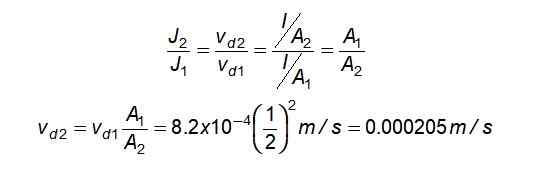Prędkość oporu jest niższa w szerszej części, której oczekiwano.

Bibliografia

1. Resnick, r. 1992.Fizyczny. Trzecie wydanie rozszerzone w języku hiszpańskim. Głośność 2. Continental Editorial Company S.DO. c.V.
2. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14^th. Wyd. Głośność 2. 817-820.
3. Serway, r., Jewett, J. 2009. Fizyka nauk i inżynierii z nowoczesną fizyką. 7. edycja. Głośność 2. Cengage Learning. 752-775.
4. Uniwersytet Sevilla. Department of Applied Physics III. Gęstość i intensywność prądu. Odzyskane od: nas.Jest
5. Walker, J. 2008. Fizyka. Czwarty edycja. osoba.725-728.