Dekodowanie wyrażeń
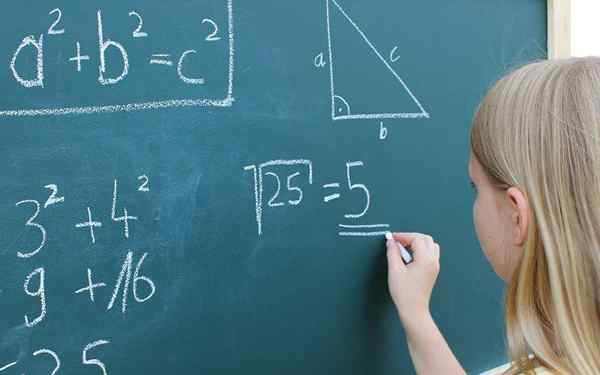
- 3594
- 682
- Maksymilian Kępa
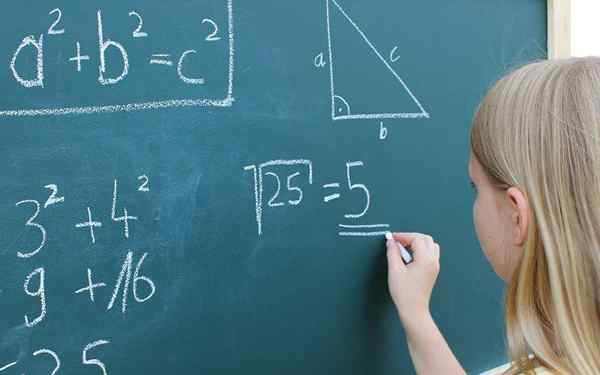 Wyrażenia matematyczne. Z licencją
Wyrażenia matematyczne. Z licencją Co to jest dekodowanie wyrażeń?
Dekodowanie wyrażeń Odnosi się do sposobu ustnego wyrażenia wyrażenia matematycznego. W matematyce, a wyrażenie, Nazywane również wyrażeniem matematycznym, jest to kombinacja dosłownych współczynników i części dosłownych poprzez inne znaki matematyczne (+, -, x, ±, /, [],), w celu utworzenia matematycznego operacji operacji.
Mówiąc prosto, współczynniki są reprezentowane przez liczby, podczas gdy część dosłowna składa się z liter (pierwsze trzy litery alfabetu, A, B i C, są zwykle używane do wyznaczenia części dosłownej).
Z kolei te „litery” reprezentują wielkości, zmienne i stałe, do których można przypisać wartość numeryczną.
Wyrażenia matematyczne składają się z terminów, które są każdym z elementów oddzielonych symbolami operacyjnymi. Na przykład następujące wyrażenie matematyczne ma cztery terminy:
5x2 + 10x + 2x + 4
Należy zauważyć, że wyrażenia mogą być ustanawiane tylko przez współczynniki, współczynniki i dosłowne części i tylko przez części dosłowne.
Na przykład:
25 + 12
2x + 2y (ekspresja algebraiczna)
3x + 4/y + 3 (irracjonalna ekspresja algebraiczna)
x + y (cała ekspresja algebraiczna)
4x + 2y2 (Cała wyrażenie algebraiczne)
Dekodowanie wyrażeń matematycznych
Dekodowanie prostych wyrażeń matematycznych
1. A + B: Suma dwóch liczb
Na przykład: 2 + 2: suma dwóch i dwóch
2. A + B + C: Suma trzech liczb
Na przykład: 1 + 2 + 3: suma jednego, dwóch i trzech
3. A - B: Odejmowanie (lub różnica) dwóch liczb
Na przykład: 2 - 2: Odejmowanie (lub różnica) dwóch i dwóch
4. A x b: iloczyn dwóch liczb
Może ci służyć: podejście problemoweNa przykład: 2 x 2: iloczyn dwóch i dwóch
5. Do ÷ B: Dwa stosunek liczb
Na przykład: 2/2: iloraz dwóch i dwóch
6. 2 (x): dwa razy liczba
Na przykład: 2 (23): dwa razy 23
7. 3 (x): potrójna liczba
Na przykład: 3 (23): potrójna 23
8. 2 (A + B): dwa razy więcej niż suma dwóch liczb
Na przykład: 2 (5 + 3): dwa razy więcej niż suma pięciu i trzech
9. 3 (A + B + C): Triple z sumy trzech liczb
Na przykład: 3 (1 + 2 + 3): potrójna suma jednego, dwóch i trzech
10. 2 (a - b): dwukrotność różnicy dwóch liczb
Na przykład: 2 (1–2): dwukrotność różnicy jednego i dwóch
jedenaście. x/2: połowa liczby
Na przykład: 4/2: połowa czterech
12. 2n + x: suma podwójnej jednej liczby i inna liczba
Na przykład: 2 (3) + 5: suma podwójnych trzech i pięciu
13. X> y: „equis” jest większy niż „ye”
Na przykład: 3> 1: trzy jest większe niż jeden
14. X < y: “Equis” es menor que “ye”
Na przykład: 1 < 3: Uno es menor que tres
piętnaście. X = y: „equis” jest równe „ye”
Na przykład: 2 x 2 = 4: Produkt dwóch i dwóch jest równy czterema
16. X2 : Kwadrat liczby lub liczby kwadratowej
Na przykład: 52 : Pięć lub pięć kwadratowych kwadratowych
17. X3: Kostka liczby lub liczby do sześcianu
Na przykład: 53: Pięć lub pięć kostki do kostki
Może ci służyć: metoda jakościowa18. (A + B)2: Kwadrat sumy dwóch liczb
Na przykład: (1 + 2)2: Kwadrat suma jednego i dwóch
19. (x - y)/2: połowa różnicy dwóch liczb
Na przykład: (2–5)/2: połowa różnicy dwóch i pięciu
20. 3 (x + y)2: Potrójne kwadratu suma dwóch liczb
Na przykład: 3 (2 + 5)2 : Potrójny kwadrat suma dwóch i pięciu
dwadzieścia jeden. (A + B)/2: Dwie liczby
Na przykład: (2 + 5)/2: dwa -i pięć półsysezmów
Dekodowanie wyrażeń algebraicznych
1. 2 x5 + 7/y + 9: [dwa equis podniesione do pięciu] więcej [siedem nad tobą] więcej [dziewięć]
2. 9 x + 7y + 3 x6 - 8 x3 + 4 y: [dziewięć equis] Więcej [siedem lat] więcej [trzy equis podniesione do sześciu] mniej [osiem equis podniesionych do 3] więcej [cztery lata]
3. 2x + 2y: [dwa equis] Więcej [dwa lata]
4. X/2 - y5 + 4y5 + 2x2: [x na 2] mniej [i podniesiony do pięciu] więcej [cztery i podniesione do pięciu] więcej [podniósł dwa kwadratowe]
5. 5/2 x + y2 + X: [pięć na dwóch equis] Więcej [i kwadrat] więcej [equis]
Dekodowanie wielomianowe
1. 2x4 + 3x3 + 5x2 + 8x + 3: [Dwa z Equis podniesionych do czterech] więcej [trzy equis podwyższone do trzech] więcej [pięć kwadratów podwyższonych] więcej [8 equis] plus trzy
2. 13 i6 + 7y4 + 9Y3 + 5Y: [trzynaście i podniesionych do sześciu] więcej [siedem z czterech] więcej [dziewięć i podwyższonych do trzech] więcej [pięciu lat]]]
3. 12Z8 - 5z6 + 7z5 + z4 - 4Z3 + 3Z2 + 9z: [dwanaście zta podwyższało do ośmiu] mniej [pięć Zety podwyższonych do sześciu] więcej [siedem Zety podniesionych do pięciu] więcej [Zeta podwyższono do czterech] minus [cztery Zeta podwyższone do kostki] więcej [trzy Zeta podniesione do kwadratu] więcej [dziewięć Zeta]
Może ci służyć: znaczenie matematyki w rozwiązywaniu sytuacji fizycznychBibliografia
- Wyrażenia z zmiennymi. Odzyskano z Khanacademy.org.
- Zrozumienie wyrażeń algebraicznych przez doświadczonych użytkowników matematyki. NCBI odzyskało.NLM.Nih.Gov.
- Pisanie wyrażeń matematycznych. Wyzdrowiał z MathGoodies.com.

