Ile kosztuje x przez x?

Mnożyć x przez x dostajesz x².

X² czyta jak "X kwadrat" Lub po prostu "X kwadrat".

Dlaczego x przez x to x²?

Wynik x przez x jest X².

Jest to bardzo łatwy wynik do weryfikacji, dzięki Właściwość mnożenia mocy równej bazy.

W algebrze litera X jest używana jako sposób na wywołanie kwoty, która wymaga nieznanych wartości, chociaż można również użyć innych liter.

Właściwość mnożenia uprawnień tej samej podstawy stwierdza, że ​​”Podczas mnożenia dwóch identycznych podstaw, ta sama baza jest zapisywana i dodaje się wykładniki".

X^Do∙ x^B = x^A+B

Wykładnik równy 1 z x jest zwykle pomijany, więc X¹ = x.

Jeśli chcemy wiedzieć, ile x przez x:

Podstawa to x (to samo jest napisane) i Wykładniki są dodawane do+B (Jego wartości są równe 1):

x ∙ x = x¹⁺¹ = x²

Przykłady właściwości mnożenia mocy równej bazy

Spójrzmy na kilka bardzo prostych przykładów numerycznych:

2 × 2 = 2² = 4

3 × 3 = 3² = 9

4 × 4 = 4² = 16

(-2) × (−2) = 2² = 4

Zauważ, że powyższy znak ujemny nie zmienia wyniku, ponieważ zgodnie z prawem znaków, pomnożenie dwóch ujemnych kwot jest uzyskiwane pozytywne.

W poprzednich przykładach użyto liczb całkowitych, ale operacja jest równie ważna dla liczb dziesiętnych, ułamkowych, rzeczywistych i złożonych.

Obszar kwadratu

Kwadrat liczby często pojawia się w obliczaniu obszarów regularnych liczb geometrycznych. Na przykład kwadrat, który jest pojedynczym wielokątem czteroosobowym, z których wszystkie mają tę samą miarę.

Może ci służyć: system równań: metody rozwiązania, przykłady, ćwiczenia

Obszar kwadratu jest podawany przez kwadrat jego boku, jeśli nazywa się „x”, wówczas obszar A kwadratu jest wart x².

Przykład obszaru kwadratu

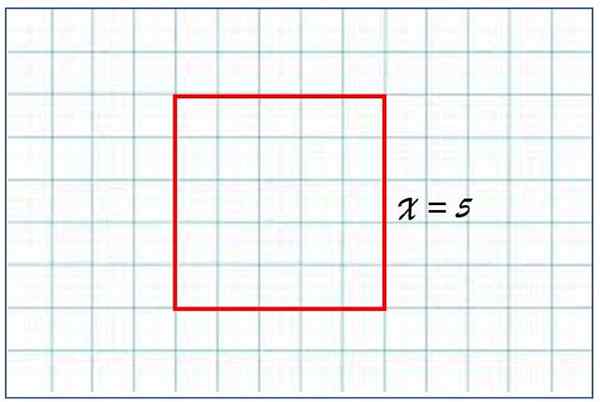
Powierzchnia kwadratowa A, której strona to x = 5 jednostek jest równa:

A = 5² = 5 × 5 = 25 jednostek obszaru

Kwadrat z boku równy 5 dowolnymi jednostkami długości ma powierzchnię 25 jednostek powierzchni. Źródło: f. Zapata.

Wynik ten ma sens, ponieważ kwadrat składa się z 5 wierszy i 5 kolumn mniejszych kwadratów, z boku równego 1. Jeśli czytelnik uważnie zaobserwuje postać, zda sobie sprawę, że czerwony plac składa się z 25 małych kwadratów jednolitego obszaru.

Ważny:

Jednostki w tym przykładzie są dowolne, mogą być metry, centymetry, cale lub inne. Tutaj nie zostały określone, ale w każdym razie odpowiedni obszar byłby podawany w metrach kwadratowych, kwadratowych, centymetrach kwadratowych lub innych. Obszar jest zawsze podawany w jednostkach o długości kwadratowej.

Kwadrat liczby ułamkowych i dziesiętnych

Aby znaleźć kwadrat liczby ułamkowej, który składa się z ponumerowanego i mianownika, oddzielonego przez linię ułamkową, konieczne jest pomnożenie licznika samego siebie, a także mianownika, uzyskiwania nowej liczby ułamkowej.

Przykłady kwadratów kwadratowych

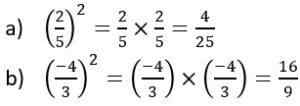
Przykłady liczb kwadratowych

Jeśli chodzi o kwadrat liczby dziesiętnej, musimy przestrzegać zasad mnożenia liczb dziesiętnych.

a) 0.6² = 0.6 × 0.6 = 0.36

b) (−0.4)² = (−0.4) × (-0.4) = 0.16

Zarówno w tym przykładzie, jak i odpowiadającym jednej z poprzedniej sekcji, obserwuje się, że kwadrat liczby ujemnej jest zawsze dodatni. Dotyczy to jeszcze mocy, nie tylko dla placu.

Może ci służyć: równoważne zestawy: co to są, wyjaśnienie, przykłady