Boltzmann Stała historia, równania, obliczenia, ćwiczenia

Boltzmann stała Jest to wartość, która dotyczy średniej energii kinetycznej układu termodynamicznego lub obiektu o temperaturze bezwzględnej tej samej. Chociaż są często zdezorientowane, temperatura i energia nie są tym samym koncepcją.

Temperatura jest miarą energii, ale nie samą energią. Z stałą Boltzmanna jest połączona ze sobą w następujący sposób:

I_C = (3/2) k_B  T

Boltzmann gospodarz w Wiedniu. Źródło: Dadotet w angielskiej Wikipedii [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/]]

To równanie jest ważne dla idealnej cząsteczki gazowej monoatomicznej M, Gdzie I_C To jego energia kinetyczna podana w dżule, K_B To jest stała Boltzmanna i T Jest to temperatura bezwzględna w Kelvin.

W ten sposób, gdy temperatura rośnie, wzrasta również średnia energia kinetyczna według cząsteczki substancji, zgodnie z oczekiwaniami. I odwrotnie dzieje się, gdy temperatura maleje, możliwość osiągnięcia punktu, w którym przestaje cały ruch, osiągana jest najniższa możliwa lub bezwzględna temperatura.

Mówiąc o średniej energii kinetycznej, należy pamiętać, że energia kinetyczna jest związana z ruchem. A cząsteczki mogą poruszać się na wiele sposobów, na przykład poruszać się, obracać lub wibrujące. Oczywiście, nie wszyscy zrobią to w ten sam sposób, a ponieważ są niezliczone, wówczas średnia jest podejmowana w celu scharakteryzowania systemu.

Niektóre stany energetyczne są bardziej prawdopodobne niż inne. Ta koncepcja ma radykalne znaczenie w termodynamice. Energia rozważana w poprzednim równaniu jest energią kinetyczną translacji. Prawdopodobieństwa państw i ich relacji z stałą Boltzmanna będzie mówić nieco później.

W 2018 r. Kelvin został na nowo zdefiniowany, a wraz z nim Boltzmann stała, która w systemie międzynarodowym wynosi około 1.380649 x 10^-23 J. K^-1. Można osiągnąć znacznie większą precyzję dla stałej Boltzmanna, która została określona w wielu laboratoriach na całym świecie, różnymi metodami.

[TOC]

Historia

Słynna stała zawdzięcza swoją nazwę fizykowi Ludwigowi Boltzmannowi (1844–1906), urodzonym w Wiedniu, który poświęcił swoje życie jako naukowca badaniu statystycznego zachowania systemów z wieloma cząsteczkami, z punktu widzenia mechaniki newtonowskiej.

Chociaż dziś istnienie atomu jest powszechnie akceptowane, w dziewiętnastym wieku przekonanie o tym, czy atom naprawdę istniał, czy był sztuką, z którą wyjaśniono wiele zjawisk fizycznych.

Może ci służyć: normalny wektor: obliczenia i przykład

Boltzmann był silnym obrońcą istnienia atomu, a w swoim czasie spotkał się z ostrą krytyką swojej pracy wielu kolegów, którzy uznali, że zawierają nierozpuszczalne paradoksy.

Oświadczył, że obserwowalne zjawiska na poziomach makroskopowych można wytłumaczyć właściwościami statystycznymi cząstek składowych, takich jak atomy i cząsteczki.

Ta krytyka może wynikać z głębokiego epizodu depresji, który doprowadził go do odebrania sobie życia na początku września 1906 r., Kiedy to miał wiele do zrobienia, ponieważ był uważany za jednego z wielkich fizyków teoretycznych swoich czasów i tam. było niewiele, że inni naukowcy przyczynią się do potwierdzenia prawdziwości swoich teorii.

Nie zdarzyło się to długo po jego śmierci, kiedy nowe odkrycia dotyczące natury atomu i jego cząstek składowych zostaną dodane, aby dać powód Boltzmannowi.

Boltzmann's Constant and Planck's Works

Teraz stała Boltzmanna k_B Został wprowadzony, jak jest znany dzisiaj po pracy austriackiego fizyka. To Max Planck, w jego prawie emisji czarnego ciała, dzieło, które przedstawił w 1901 r., Dał mu wartość 1,34 x 10²³ J/k.

Do 1933 r. Boltzmann został dodany do Wiednia jako hołd plakatowy tablica z definicją entropii obejmującej słynną stałą: S = k_B Log w, równanie, które zostanie omówione później.

Dziś stała Boltzmanna jest niezbędna w stosowaniu praw termodynamicznych, mechaniki statystycznej i teorii informacji, których pola, które ten fizyk ze smutnym końcem był pionierem.

Wartość i równania

Gazy można opisać w kategoriach makroskopowych, a także w kategoriach mikroskopowych. Dla pierwszego opisu istnieją pojęcia, takie jak gęstość, temperatura i ciśnienie.

Należy jednak pamiętać, że gaz składa się z wielu cząstek, które mają globalną tendencję do pewnego zachowania. To ten trend jest mierzony makroskopowo. Jednym ze sposobów określenia stały Boltzmanna jest dzięki dobrze znanym równaniu gazów idealnych:

P.V = n. R. T

Tutaj P To ciśnienie gazowe, V To jego głośność, N Jest to liczba obecnych moli, R Jest to stała gazów i T To jest temperatura. W mol z gazu idealnego spełnia się następujący związek między produktem P.V, i energia kinetyczna tłumaczenia K Cały zestaw to:

Może ci służyć: korpusowy model materii

P.V = (2/3). K

Dlatego energia kinetyczna jest:

K = (3/2) n.R.T

Dzieląc przez całkowitą liczbę obecnych cząsteczek, które będą nazywane n, uzyskuje się średnią energię kinetyczną pojedynczej cząstki:

I_C = K /n

I_C= (3/2N) n.R.T

W mol istnieje liczba cząstek n_DO, I dlatego całkowita liczba cząstek jest N = nnA, pozostanie:

I_C = (3/2NN_DO) N.R.T

Dokładnie iloraz R/n_DO Jest to stała Boltzmanna, wykazana, że ​​energia kinetyczna średniej translacji cząstki zależy tylko od temperatury bezwzględnej, a nie innych wielkości, takich jak ciśnienie, objętość lub nawet rodzaj cząsteczki:

I_C = (3/2) k_B. T

Stała i entropia Boltzmanna

Gaz ma daną temperaturę, ale temperatura ta może odpowiadać różnym wewnętrznym stanom energii. Jak wizualizować tę różnicę?

Rozważ jednoczesne uruchomienie 4 monet i sposobów, w jakie mogą upaść:

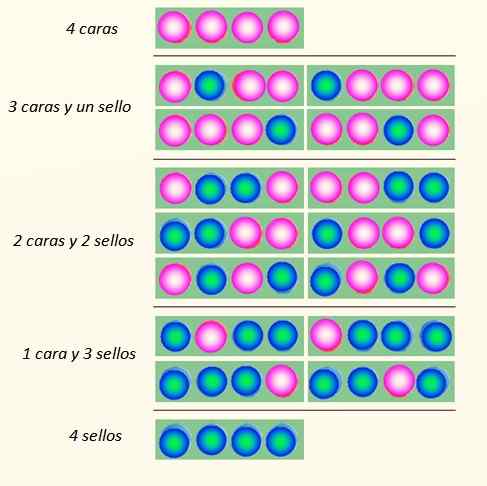Sposoby, w jakie 4 monety mogą spaść. Źródło: Self Made

Zestaw monet może przyjąć w sumie 5 stanów, które są rozważane Makroskopijny, opisane na rysunku. Który z tych stanów czytelnik powiedziałby, że jest to najbardziej prawdopodobne?

Odpowiedź powinna być stan 2 powierzchni i 2 krzyże, ponieważ ma ona łączną 6 możliwości, 16 ilustrowanych na rysunku. I 2⁴ = 16. Są one równoważne państwom mikroskopijny.

A co, jeśli uruchomi się 20 monet zamiast 4? Byłoby w sumie 2²⁰ możliwości lub „stany mikroskopowe”. Jest to znacznie większa i trudniejsza liczba. Aby ułatwić zarządzanie dużą liczbą, logarytmy są bardzo odpowiednie.

Teraz wydaje się, że państwo z największym zaburzeniem jest najbardziej prawdopodobne. Najczęściej uporządkowane stany, takie jak 4 twarze lub 4 znaczki, są nieco mniej prawdopodobne.

Entropia stanu makroskopowego S jest zdefiniowana jako:

S = k_B Ln w

Gdzie W Jest to liczba możliwych stanów mikroskopowych i k_B To jest stała Boltzmanna. Jak Ln w Jest bezwymiarowy, entropia ma takie same jednostki co k_B: Joule/k.

To jest słynne równanie w nagrobku Boltzmanna w Wiedniu. Jednak bardziej niż entropia istotna jest jej zmiana:

Może ci służyć: zmienne termodynamiczne: które są i ćwiczenia rozwiązane

ΔS = k_B Ln w₂ - k_B Ln w₁ = k_B LN (w₂/w₁)

Jak oblicza się K_B?

Wartość stałej Boltzmanna jest uzyskiwana eksperymentalnie precyzyjnie z pomiarami opartymi na Termometria akustyczna, które są przeprowadzane za pomocą właściwości, która ustanawia zależność od prędkości dźwięku w gazie o temperaturze tej samej.

Rzeczywiście, prędkość dźwięku w gazie jest podana przez:

Gdzie b _Adiabatyczne Jest to adiabatyczny moduł ściśliwości podany przez:

B_Adiabatyczne = γP

A ρ to gęstość gazu. Dla poprzedniego równania, P Jest to ciśnienie omawianego gazu i γ Jest to współczynnik adiabatyczny, którego wartość dla określonego gazu znajduje się w tabelach.

Instytuty metrologiczne doświadczają również innych sposobów pomiaru stałej, takich jak Johnson Noise Thermometry, który wykorzystuje fluktuacje termiczne, które występują losowo w materiałach, w szczególności u sterowników.

Rozwiązane ćwiczenia

-Ćwiczenie 1

Znajdować:

a) Energia kinetyczna średniej tłumaczenia I_C który ma idealną cząsteczkę gazową w temperaturze 25 ° C

b) energia kinetyczna tłumaczenia K cząsteczek w 1 mol tego gazu

c) Średnia prędkość cząsteczki tlenu w temperaturze 25 ° C

Fakt

M_tlen = 16 x 10 ^-3 kg/mol

Rozwiązanie

Do) I_C = (3/2) k t = 1.5 x 1.380649 x 10^-23J. K^-1 x 298 k = 6.2 x 10^{-dwadzieścia jeden} J

B) K = (3/2) n.R.T = 5 x 1 mol x 8.314 J/mol .K x 298 k = 3716 j

C) I_C = ½ mV², Biorąc pod uwagę, że cząsteczka tlenu jest dwuatomiczna, a masę molową musi zostać pomnożona przez 2, będzie:

-Ćwiczenie 2

Znajdź zmianę entropii, gdy 1 mol gazu zajmował objętość 0.5m³ Rozszerza się, aby zajmować 1 m³.

Rozwiązanie

ΔS = k_B LN (w₂/w₁)

W₂= 2^NW₁ (Było 2⁴ Pamiętaj, że stany mikroskopowe do uruchomienia 4 monet?)

Gdzie n jest liczbą cząstek obecnych w 0.5 mol gazu 0.5 x n_DO:

ΔS = k_B LN (2^N W₁/w₁) = k_B LN 2^N= k_B 0.5n_DO LN 2 = 2.88 J/k

Bibliografia

1. Atkins, str. 1999. Chemia fizyczna. Omega Editions. 13-47.
2. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 664-672.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th ... Ed Prentice Hall. 443 -444.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. 647-673.
5. Jeśli redefinicja. Kelvin: Boltzmann Constant. Odzyskane z: NIST.Gov