Ochrona zasady momentu liniowego, przykładów, ćwiczeń.

Ochrona pędu liniowego ciała ustala, że ​​iloczyn jego masy przez wektor prędkości jest stałą ilością, gdy ciało jest wolne od interakcji z innymi ciałami i z prędkością mierzoną w odniesieniu.

Kiedy istnieje kilka ciał, które oddziałują tylko między nimi, ale nie ze środowiskiem zewnętrznym, to pęd Zestaw pozostaje również stały w czasie.

Astronauta w kosmosie jest wolna od wszystkich interakcji, a zatem jego liniowy moment

Moment liniowy, ilość ruchu liniowego lub po prostu pęd, Jest oznaczony listem P I jest to kwota wektora:

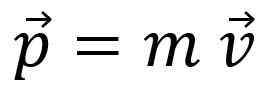
Moment liniowy nie jest taki sam jak prędkość, chociaż współczynnik jest widoczny: na przykład ciężarówka, która przechodzi do 20 km/h, ma więcej czasu liniowego niż rower, który porusza się z tą samą prędkością.

Aby zmienić się liniowy moment ciała, konieczne jest, aby działała na nią siła zewnętrzna netto, w przeciwnym razie pozostała stała. Ponadto moment liniowy P systemu utworzonego przez N-Body Jest to suma wektorowa poszczególnych momentów:

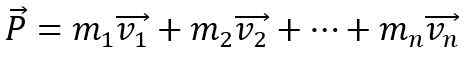
[TOC]

Zasada ochrony ilości ruchu liniowego

W ciele wolnym od sił (lub takich, w których wszystkie siły na nim są anulowane) zdarza się, że moment liniowy.

W ten sam sposób przechodzi w systemie utworzonym przez kilka ciał, które oddziałują tylko ze sobą, ale nie ze środowiskiem zewnętrznym: całkowity moment liniowy systemu pozostaje ustalony podczas ewolucji zestawu zestawu.

Ta zasada ochrony jest taka:

Całkowity liniowy moment zestawu N-Body, który oddziałuje tylko ze sobą, ale nie ze środowiskiem zewnętrznym, jest niezmienną ilością w czasie.

I matematycznie wyraża się to w następujący sposób:

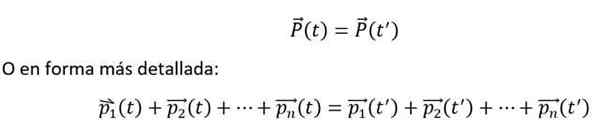
Poprzednia równość jest spełniona, jeśli i tylko wtedy N-ciała wchodzą w interakcje ze sobą, ale nie ze środowiskiem zewnętrznym. Ponadto poszczególne momenty należy zawsze mierzyć w odniesieniu do systemu odniesienia bezwładnego.

Przykłady

Przykład 1

Dwóch astronautów w kosmosie są pobierane z rąk i pozostają w ustalonej pozycji w odniesieniu do statku. Ale pchają się nawzajem, zaczynają się rozdzielić w przeciwnych kierunkach, kiedy są widoczne ze statku.

Może ci służyć: teoria Wielkiego Wybuchu: cechy, etapy, dowody, problemy

W tym przypadku, ponieważ interakcja między astronautami jest tylko wśród nich poprzez siłę kontaktową ich rąk, całkowity moment liniowy. To znaczy całkowity czas liniowy 0.

Jednak liniowy moment każdego astronauta zmienił się. Początkowo każdy miał moment liniowy 0 w odniesieniu do statku, ale po pchaniu jednego wychodzi w jednym kierunku, a drugi w przeciwnym kierunku, z liniowymi momentami liniowymi o równej wielkości i przeciwnych adresach.

Zatem, gdy poszczególne momenty są dodawane wektorowo, w rezultacie otrzymuje się początkowy całkowity pęd liniowy, który jest nieważny.

Z drugiej strony zachowanie ilości momentu liniowego. Ale wynik pomnożenia jej masy przez jej prędkość jest równa produktowi uzyskane przez pomnożenie masy drugiej przez prędkość drugiego.

Przykład 2

Szczeniak znajduje się na pływającej platformie w jeziorze spokojnych wód, a jego właściciel widzi go z doku. Na początku zarówno platforma, jak i szczeniak są w spoczynku, ale kiedy szczeniak chce zbliżyć się do właściciela, platforma odsuwa się od doku.

Wyjaśnienie tej obserwacji jest dokładnie w zasadzie ochrony liniowej ilości pędu. System składa się z szczeniaka i platformy.

Szczeniak może chodzić po platformie dzięki sile tarcia między nogami a powierzchnią, w tym przypadku siła tarcia jest wewnętrzną siłą interakcji między nią a platformą.

Zestaw jest izolowanym systemem, a platforma może poruszać się poziomo po jeziorze, wolnym od oporu ruchu. Z drugiej strony, w kierunku pionowym wszystkie siły są równoważone i kompensowane, a zestaw nie ma ruchu w tym kierunku.

Dlatego w tej sytuacji wszystkie hipotezy są spełnione, aby zastosować zasadę ochrony pędu liniowego.

Przykład 3

Eskimo zostaje złapane na środku lodów, lód jest tak gładki, że bez względu na to, ile wypróbowywano, Eskimo poślizgnie się i zawsze pozostaje w tym samym miejscu.

Jedynym możliwym sposobem opuszczenia jeziora Eskimosów jest to, że leży on w kierunku, w którym ciężki obiekt niesie plecak (zakładając jeden).

Może ci służyć: optyka geometryczna: jakie badania, prawa, zastosowania, ćwiczenia

Aplikacje

Wysłać w kosmosie

Ochrona momentu liniowego. W tym przypadku impuls statku osiąga się przez wydalenie gazów z dużą prędkością, aby rakieta mogła poruszać się w przeciwnym kierunku, do którego zostały wydalone.

Jeśli statek jest pierwotnie w spoczynku, gdy paliwo zostaje spalone i wydalone, siła wydalenia występuje przeciwko samemu statkowi. Jest to siła wewnętrzna między gazami a statkiem. Nie ma sił zewnętrznych i dlatego stosuje ochronę momentu liniowego.

Ponieważ liniowy moment gazów jest taki sam i sprzeczny z momentem statku, udaje się opuścić odpoczynek, a kontynuując wydalenie gazów, zwiększa jego ruch, a zatem prędkość.

Życie codzienne

Kolejny przypadek ochrony momentu liniowego.

Można argumentować, że w tym przypadku zasada nie ma zastosowania, ponieważ istnieje siła zewnętrzna: opór oferowany przez drewno.

Jednak w momencie kontaktu siła, którą młot wydrukuje do paznokcia, jest siłą wewnętrzną (między systemem, który jest gwoździem a młotkiem) znacznie większą niż odporność, której przeciwstawia się drewno, a zatem ten ostatni jest nieistotny.

Cały liniowy moment młotka, który jest dość duży ze względu na jego wielką masę i prędkość, jest przenoszony do paznokcia tuż po zderzeniu. Zwróć uwagę, że cały moment jest przenoszony, ale nie cała energia kinetyczna młotka, ponieważ jego część jest przekształcana w energię cieplną w gwoździe i młot, który podnosi temperaturę po uderzeniu.

Ćwiczenia

Ćwiczenie 1

Andrew i astronauci Berenice są poza stacją kosmiczną pobraną z obu rąk i w spoczynku w odniesieniu do stacji. Jeżdżą, pchają ręce na ręce innych i są zwolnione. Jeśli Andrew, 70 kg masy porusza się na 1 m/s w odniesieniu do stacji, jaka jest prędkość Berenice z 49 kg masy?

Rozwiązanie

W tym przypadku hipoteza zachowania pędu liniowego jest wyraźnie stosowana, ponieważ w przestrzeni zewnętrznej nie ma sił zewnętrznych. Siła, z jaką ich dłonie popychają obu astronautów, jest siłą wewnętrzną.

Może ci służyć: dyfrakcja fali: koncepcja i przykłady

Załóżmy, że Msza Andrzeja to m_Do i berenice m_B. Podobnie prędkości obu po impulsie są V_Do Dla Andrew i V_B Dla berenice. Wówczas konserwacja pędu liniowego jest stosowana w następujący sposób:

M_Do∙0 + M_B∙0 = M_Do∙V_Do+ M_B∙V_B

Oczyszczanie prędkości Berenice:

V_B = - (m_Do / M_B) ∙ V_Do

Umieszczenie wartości numerycznych:

V_B = - (70 /49) ∙ (1 m / s) Lub = -1,43 m/s Lub

To znaczy, że Berenice porusza się szybko 1,43 m/s w przeciwnym kierunku Andrew.

Ćwiczenie 2

Szczeniak podchodzi do swojego właściciela na częściowo-sylikowanej platformie. Źródło: f. Zapata.

Ciasto o pojemności 5 kg spoczywa na platformie 15 kg, która unosi się, również w spoczynku, na nieruchomym jeziorze. Jeśli szczeniak zacznie chodzić po platformie z prędkością 0,5 m/s w odniesieniu do tego. Jak szybko szczeniak i platforma dotycząca ustalonego obserwatora do uziemienia?

Rozwiązanie

Zostanie uznany za bezwładowy system referencyjny do dok, w którym jest właściciel szczeniaka. Początkowo zarówno szczeniak, jak i pływająca platforma są w odniesieniu do stacji dokującej.

Kiedy szczeniak postanawia szybko iść w stronę właściciela V ' Jeśli chodzi o platformę, platforma odsuwa się od sprężyny z prędkością +V. Szybkość szczeniaka w odniesieniu do doku jest osiągana przez sumę wektora jego prędkości w odniesieniu do platformy oraz prędkość platformy i oznacza ją przez:

v = -v' + V

Ponieważ odporność wody na ruch platformy jest praktycznie zerowy ze względu na jej niską prędkość, można potwierdzić, że system złożony Szczeniak + platforma Jest to izolowany system i stosuje się zasadę zachowania pędu liniowego:

0 = m ∙ v + m ∙ v

Pamiętając, że masz v = v ' + v:

0 = -m ∙ v ' + m ∙ v + m ∙ v

To znaczy: m ∙ v '= (m+m) ∙ v

Dlatego v = [m/(m + m)] v 'y v = - (m/m) v = - [m/(m + m)] v'

Zastąpienie wartości numerycznych to:

V = [5/(5 +15)] ∙ 0,5 m/s = 0,125 m/s

To jest prędkość, z jaką odsuwa się platforma wiosenna.

V = -(15/20) ∙ 0,5 m/s = -0 375 m/s

I to jest prędkość, z jaką szczeniak zbliża się do doku.

Bibliografia

1. Uniwersytet Duke. Układy cząstek. Odzyskane z: Webhome.Phy.Książę.Edu.
2. Rex, a. 2011. Podstawy fizyki. osoba.
3. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. osoba.
4. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.
5. Tipler, str. (2006). Fizyka nauk i technologii. Ed. Tom 1. Redakcja Reverted.