Elastyczne wstrząsy w wymiarze, specjalne przypadki, ćwiczenia

Elastyczne wstrząsy o Elastyczne zderzenia składają się z krótkich, ale intensywnych interakcji między obiektami, w których zachowuje się zarówno ilość ruchu, jak i energia kinetyczna. Choques to bardzo częste zdarzenia w naturze: od cząstek subatomowych po galaktyki, przechodząc przez piłki bilardowe i samochody wstrząsowe w parkach przyciągających, wszystkie są przedmiotami zdolnymi do zderzenia.

Podczas kolizji lub szoku siły interakcji między obiektami są bardzo intensywne, znacznie więcej niż te, które mogą działać zewnętrznie. W ten sposób można potwierdzić, że podczas zderzenia cząstki tworzą izolowany układ.

Zderzenia między piłkami bilardowymi można uznać za sprężyste. Źródło: Pixabay.

W takim przypadku jest spełnione, że:

Gdzie P Jest to wektorowa ilość ruchu, której wielkość jest Mv (Masa prędkości). Jeśli pochodna P jest null, to znaczy P To jest stałe. A to oznacza, że ​​nie różni się, że jest zachowane. Dlatego możemy potwierdzić, że:

P_albo = P_F

Ilość ruchu P_albo Przed kolizją jest taka sama jak po zderzeniu. Jest to spełnione dla każdej kolizji typu, zarówno elastycznego, jak i nieelastycznego.

Teraz musisz rozważyć następujące czynności: Podczas kolizji obiekty doświadczają pewnego deformacji. Gdy starcie jest sprężyste, obiekty szybko odzyskują swoją oryginalną formę.

[TOC]

Ochrona energii kinetycznej

Zwykle podczas szoku część energii obiektów jest wydawana na ciepło, deformacja, dźwięk, a czasem nawet na wytwarzanie światła. Tak więc energia kinetyczna systemu po zderzeniu jest mniejsza niż oryginalna energia kinetyczna.

Kiedy energia kinetyczna k, jest zachowana:

K_albo = K_F

Co oznacza, że ​​siły działające podczas kolizji są konserwatywne. Podczas gdy kolizja trwa, energia kinetyczna jest krótko przekształcana w energię potencjalną, a następnie znów jest energią kinetyczną. Odpowiednie energie kinetyczne różnią się, ale suma pozostaje stała.

Idealnie elastyczne zderzenia nie są częste, chociaż piłki bilardowe są dość dobrym podejściem, a także zderzenia, które mają miejsce między idealnymi cząsteczkami gazu.

Elastyczne wstrząsy w wymiarze

Przeanalizujmy zderzenie dwóch cząstek tego w jednym wymiarze; To znaczy cząstki, które oddziałują, powiedzmy, wzdłuż osi x. Załóżmy, że mają masy M₁ I M₂. Początkowe prędkości każdego z nich są Lub₁ I Lub₂ odpowiednio. Ostateczne prędkości są v₁ I v₂.

Możemy się obejść bez zapisu wektora, ponieważ ruch jest przeprowadzany wzdłuż osi x, jednak znaki (-) i (+) wskazują znaczenie ruchu. Po lewej stronie jest negatywne i pozytywne, według konwencji.

Może ci służyć: sieci Bravais: koncepcja, cechy, przykłady, ćwiczenia

-Formuły elastycznych zderzeń

Dla ilości ruchu

M₁Lub₁ + M₂Lub₂ = m₁v₁ + M₂v₂

Dla energii kinetycznej

½ m₁Lub²₁ + ½ m₂Lub²₂ = ½ m₁v²₁ +  ½ m₂v²₂

Ilekroć znane są początkowe masy i prędkości, możliwe jest przegrupowanie równań w celu znalezienia końcowych prędkości.

Problem polega na tym, że w zasadzie jest konieczne. Idealnym byłoby znalezienie wyrażeń, które ich nie zawierają.

Pierwszym z nich jest obejście bez współczynnika ½ i przemieszczenie obu równań w taki sposób, aby pojawił się znak ujemny, a masy mogą być czynnikiem:

M₁Lub₁ - M₁v₁ = M₂v₂ - M₂Lub₂

M₁Lub²₁ - M₁v²₁  = +M₂v²₂ - M₂Lub²₂

Wyrażone w ten sposób:

M₁(Lub₁ - v₁ ) = m₂(v₂ - Lub₂)

M₁(Lub²₁ - v²₁ ) = m₂ (v²₂ - Lub²₂)

Uproszczenie w celu wyeliminowania kwadratów z prędkości

Teraz musisz użyć znaczącego produktu, zwiększa jego różnicę w drugim równaniu, które uzyskuje wyrażenie, które nie zawiera kwadratów, jak pierwotnie chciał:

M₁(Lub₁ - v₁ ) = m₂(v₂ - Lub₂)

M₁(Lub₁ - v₁ ) (Lub₁ + v₁ ) = m₂ (v₂ - Lub₂) (v₂ + Lub₂)

Następnym krokiem jest zastąpienie pierwszego równania w drugim:

M₂(v₂ - Lub₂) (Lub₁ + v₁ ) = m₂ (v₂ - Lub₂) (v₂ + Lub₂)

A kiedy termin jest powtarzany M₂(v₂ - Lub₂) Po obu stronach równości termin ten jest anulowany i jest taki:

(Lub₁ + v₁) = (V₂ + Lub₂)

Lub nawet lepiej:

Lub₁ - Lub₂= v₂ -  v₁

Ostateczne prędkości v₁ i v₂ cząstek

Teraz istnieją dwa równania liniowe, z którymi łatwiej jest pracować. Umieścimy je ponownie poniżej drugiego:

M₁Lub₁ + M₂Lub₂ = m₁v₁ + M₂v₂

Lub₁ - Lub₂= v₂ -  v₁

Mnożenie drugiego równania przez M₁ A dodanie terminu do terminu pozostaje:

M₁Lub₁ + M₂Lub₂ = m₁v₁ + M₂v₂

M₁Lub₁ - M₁Lub₂= m₁v₂ - M₁ v₁

-

2 m₁Lub₁ + (M₂ - M₁) Lub₂ = (m₂ + M₁) v₂

I jest już możliwe do wyczyszczenia v₂. Na przykład:

Podobne leczenie można wykonać, aby znaleźć równanie dla v₁. Czytelnik pozostawia się jako ćwiczenie, aby pokazać:

Specjalne przypadki w elastycznych kolizjach

Teraz, gdy równania są dostępne dla końcowych prędkości obu cząstek, nadszedł czas, aby przeanalizować niektóre specjalne sytuacje.

Dwie identyczne masy

Następnie M₁ = m₂ = m I:

v₁ = u₂

v₂ = u₁

Cząstki po prostu wymieniają swoje prędkości po zderzeniu.

Dwie identyczne masy, z których jedna była początkowo w spoczynku

Ponownie  M₁ = m₂ = m i zakładając, że Lub₁ = 0:

v₁ = u₂

v₂ = 0

Po awarii cząstka, która była w spoczynku, nabywa tę samą prędkość cząstki, która się poruszała, i to z kolei zatrzymuje się.

Może ci służyć: ciśnienie hydrauliczne

Dwie różne masy, jedna początkowo w spoczynku

Załóżmy, że w tym przypadku Lub₁ = 0, Ale masy są różne:

Co jeśli M₁ jest znacznie większy niż M₂?

Zdarza się, że m₁ Trzymaj się w spoczynku i M₂ Jest zwracany z tą samą prędkością, z jaką wpłynęło.

Huygens-Newton Współczynnik lub zasada

Wcześniej wywnioskowano następującą zależność między prędkościami dla dwóch obiektów w kolizji elastycznej: Lub₁ - Lub₂ = v₂ -  v₁. Różnice te to względne prędkości przed i po zderzeniu. Ogólnie rzecz biorąc, dla zderzenia się spełnia, że:

Lub₁ - Lub₂ = -(v₁ -  v₂)

Względna koncepcja prędkości jest lepiej doceniana, jeśli czytelnik wyobraża sobie, że jest on na jednej z cząstek, a z tej pozycji obserwuje prędkość, z jaką porusza się druga cząstka. Poprzednie równanie jest przepisane w ten sposób:

Jeśli energia kinetyczna nie zostanie zachowana, wskazany iloraz będzie mniejszy niż 1. Zadzwońmy I do wartości wspomnianego ilorazu bezwymiarowego:

O Cóż:

Wartość I ma od 0 do 1 i nazywa się Współczynnik restytucji. Gdy starcie jest sprężyste, e = 1. Kiedy jest całkowicie nieelastyczne, e = 0, podczas gdy ma jakąkolwiek inną wartość pośrednią, pewna energia kinetyczna rozproszyła się w innych rodzajach energii.

Rozwiązane ćwiczenia

-Ćwiczenie rozwiązane 1

Bilardowa kulka porusza się w lewo przy 30 cm/s, zderzając się z przodu z kolejną identyczną piłką, która porusza się po prawej stronie do 20 cm/s. Dwie kule mają to samo ciasto, a awaria jest idealnie elastyczna. Znajdź prędkość każdej piłki po uderzeniu.

Rozwiązanie

Lub₁ = -30 cm/s

Lub₂ = +20 cm/s

Jest to szczególny przypadek, w którym dwie identyczne masy zderzają się w wymiarze elastycznie, dlatego prędkości są wymieniane.

v₁ = +20 cm/s

v₂ = -30 cm/s

-Ćwiczenie rozwiązane 2

Współczynnik restytucji piłki, która odbija się na ziemi, wynosi 0,82. Jeśli upadniesz z odpoczynku, jaki ułamek twojej pierwotnej wysokości dotrze do piłki po odbiciu? I po 3 zbiórkach?

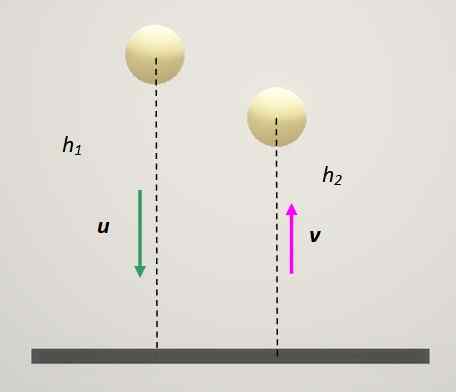Piłka odbija się na twardej powierzchni i traci wysokość z każdym odbiciem. Źródło: Self Made.

Rozwiązanie

Gleba może być przedmiotem 1 w równaniu współczynnika zwrotu. I zawsze jest w spoczynku, aby:

Wybrany jest negatywny kierunek i dodatni. Prędkość obiektu, który jest swobodnie uwalniany z określonej wysokości H_albo Jest:

Znak (-) wskazuje, że piłka schodzi:

Może ci służyć: eksperyment Torricelli: miary ciśnienia atmosferycznego, znaczenie

 

Z tą prędkością podskakując:

 

Znak + wskazuje, że jest to prędkość rosnąca. I zgodnie z nim piłka osiąga maksymalną wysokość:

 

Teraz powraca na ziemię z prędkością tej samej wielkości, ale przeciwny znak:

I odbija się z:

Osiąga to maksymalną wysokość:

Dotrzyj ponownie do ziemi z:

Kolejne zbiórki

Za każdym razem, gdy piłka odbija się i wznosi się, musisz ponownie pomnożyć prędkość przez 0.82:

I osiąga maksymalną wysokość określoną przez kwadrat o wspomnianej prędkości:

W tym momencie H₃ to około 30% H_albo. Jaka byłaby wysokość na 6. zbiórach bez konieczności wykonywania obliczeń tak szczegółowych jak poprzednie?

byłbym H₆ = 0.82¹² H_albo = 0.092H_albo lub tylko 9% H_albo.

-Ćwiczenie rozwiązane 3

Blok o powierzchni 300 g porusza się na północ do 50 cm/s i starają się z blokiem 200 g, który jest skierowany na południe 100 cm/s. Załóżmy, że starcie jest idealnie elastyczne. Znajdź prędkości po uderzeniu.

Dane

M₁ = 300 g; Lub₁ = + 50 cm/s

M₂ = 200 g; Lub₂ = -100 cm/s

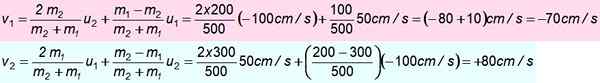
-Ćwiczenie rozwiązane 4

Uwolniona jest masa M₁ = 4 kg z punktu wskazanego na torze bez tarcia, dopóki nie zderzy się z M₂ = 10 kg w spoczynku. Do tego, czym jest wysokość m₁ Po zderzeniu?

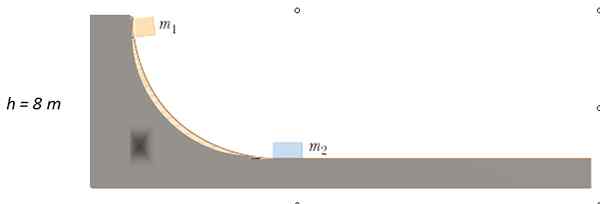
Rozwiązanie

Ponieważ nie ma tarcia, energia mechaniczna jest zachowana w celu znalezienia prędkości Lub₁ z czym M₁ wpływ  M_2. Początkowo energia kinetyczna wynosi 0, ponieważ M₁ część reszty. Podczas poruszania się po poziomej powierzchni nie ma wysokości, więc energia potencjalna wynosi 0.

MGH = ½ MU₁ ²

 

Lub₂ = 0

Teraz prędkość M₁ Po zderzeniu:

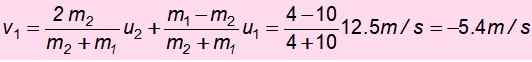
Znak ujemny oznacza, że ​​został zwrócony. Z tą prędkością wznoszą się i energia mechaniczna jest ponownie zachowana, aby znaleźć H ', Wysokość, na której udaje się wznieść po katastrofie:

½ mV₁² = MGH '

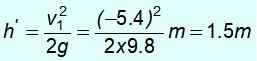
Zauważ, że nie wracasz do punktu początkowego na wysokości 8 m. Nie ma wystarczającej ilości energii, ponieważ dał część swojej energii kinetycznej masa M_1.

Bibliografia

1. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Podstawy fizyki. osoba. 135-155.
3. Serway, r., Vulle, c. 2011. Podstawy fizyki. 9^na Cengage Learning. 172-182
4. Tipler, str. (2006) Physics for Science and Technology. Ed. Tom 1. Redakcja Reverted. 217-238
5. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. MacGraw Hill. 185-195