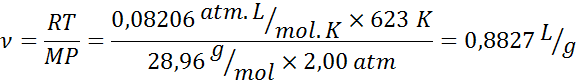Specyficzna objętość

Wyjaśniamy, jaka jest konkretna objętość, jej wzór, jednostki, jak jest obliczane i podajemy kilka przykładów obliczeń

Jaki jest konkretny tom?

On Specyficzna objętość (Reprezentowany z symbolem ν, grecka litera nu) jest intensywną właściwością materii, która mierzy objętość zajmowaną na jednostkę masy ciała. Odpowiada związku między objętością a masą, więc reprezentuje odwrotność gęstości. Oznacza to, że im gęstszy korpus, tym niższa jego objętość i odwrotnie.

Znajomość konkretnej objętości substancji jest ważna w aplikacjach, w których dostępny objętość jest ograniczona. Na przykład, wybierając paliwo do rakiety kosmicznej, ideałem jest to, że paliwo ma jako konkretną możliwą objętość, ponieważ w przeciwnym razie zajmie zbyt dużo miejsca, co będzie wymagało bardzo dużej i drogiej rakiety.

Szczegółowe objętości mają również ogromne znaczenie w dziedzinie termodynamiki, ponieważ pozwalają po prostu obliczyć objętości molowe różnych substancji z jej masy molowej lub określić całkowitą objętość próbki z jej masy.

Wreszcie, specyficzne zmiany objętości umożliwiają również zmiany faz, takie jak fuzja i gotowanie, między innymi.

Specyficzny wzór objętościowy

Poniższe równanie odpowiada matematycznej definicji określonego objętości:

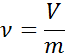
Gdzie v jest objętością ciała lub substancji, M jest jego masą, a ν jest specyficzną objętością. Można go jednak również obliczyć na podstawie gęstości, ponieważ, jak wspomniano powyżej, objętość specyficzna jest odwrotnością gęstości:

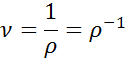
Gdzie ρ reprezentuje gęstość.

Określone jednostki głośności

Określone jednostki głośności to jednostki głośności na jednostkach masy. Jak zwykle, wielkości te można wyrażać w różnych systemach jednostek, więc specyficzna objętość może być również wyrażona w różnych jednostkach.

Może ci służyć: elektrofil: reakcje, przykłady, elektrofiliczność

Poniższa tabela pokazuje określone jednostki głośności w najważniejszych systemach jednostek:

System jednostkowy	Określone jednostki głośności
S.Siema.	M3/kg
MKS	M3/kg
CGS	CM3/g
System anglo -sakonu	Pie3/lb
Inne jednostki	ML/G lub CM3/G

Obliczanie objętości specyficzne

Dla zwykłych substancji stałych

W przypadku zwykłych ciał stałych najłatwiejszym sposobem określenia specyficznej objętości jest określenie objętości na podstawie wymiarów stałego, a następnie podzielenie między masą.

Aby określić objętość ciała stałego, wzór objętościowy odpowiadający konkretnej formie stałej (kula, stożka, cylinder itp.).

Przykład 1: Bar cylindryczny

Masz stały cylindryczny pręt o grubości 2,54 cm, 10 cm długości i masę 1,50 kg. Określ specyficzną objętość materiału w jednostkach S.Siema.

• Rozwiązanie: Jak wiemy, jest to cylinder, więc musimy użyć wzoru objętościowego cylindra, a następnie zastosować określoną formułę objętościową. Oba równania można łączyć w jednym, jak pokazano poniżej:

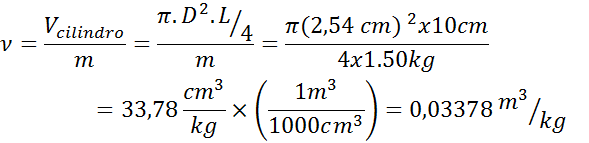
Przykład 2: Szklana kula

Szklany marmur o średnicy 1 cm jest ważony w równowadze. Ten odczyt 2,50 g. Określ konkretną objętość szkła.

• Rozwiązanie: Od średnicy wiadomo, że promień kuli wynosi 0,50 cm. Z tym promieniem i przy użyciu wzoru objętości kuli możemy określić objętość marmuru. Następnie używamy specyficznej formuły głośności. Możesz także połączyć oba równania w jednym:

Może ci służyć: trójtlenek arsenu (AS2O3)

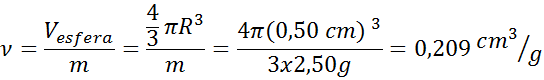
Dla amorficznych ciał stałych

W przypadku amorficznych ciał stałych nie jest możliwe określenie jego objętości za pomocą formuł, ponieważ nie jest to zwykłe ciałę stałe. Możliwym rozwiązaniem jest określenie objętości ciała za pomocą objętości, która wypiera się podczas zanurzenia w wodzie lub innej cieczy:

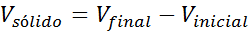
Przykład 3: Meteoryt

Meteoryt został znaleziony bardzo dziwnie. Najpierw ważył, po czym uzyskano masę 185,3 g. Następnie wprowadzono go do cylindra absolwentowego zawierającego 50,0 ml wody. Po zanurzeniu meteorytu poziom wody wzrósł do 73,5 ml. Określ specyficzną objętość meteorytu.

• Rozwiązanie: Jak wspomniano powyżej, objętość meteorytów jest określana przez przesunięcie cieczy. Różnica między objętościami wody w cylindrze stopniowym przed i po zanurzeniu meteoryt. Następnie stosuje się formułę objętościową:

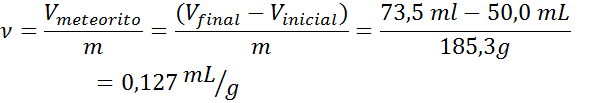
Przykład 4: Rock

W pobliżu miejsca, w którym znaleziono meteoryt poprzedniego przykładu, znaleziono kolejną skałę z podobnym wyglądem. Zważono to również, uzyskując masę 125 g i zanurzono się w wodzie, gdzie przesunęła 15,90 ml cieczy. Ustalić, czy jest to fragment meteorytowy.

• Rozwiązanie: Konkretny tom jest właściwością intensywną, więc jeśli skała jest wykonana z tego samego materiału co meteoryt, powinien mieć ten sam konkretny objętość.

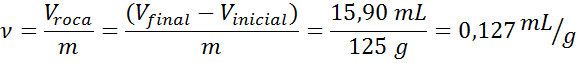
Jak widać, specyficzna objętość skały jest identyczna z objętością meteorytu, więc możliwe jest, że skała jest fragmentem.

Może ci służyć: nitrobenzen (C6H5N2): Struktura, właściwości, zastosowania, ryzyko

Płyn

Oblicz specyficzną objętość cieczy odbywa się w taki sam sposób, jak pokazano w poprzednich przykładach. Objętość można łatwo zmierzyć za pomocą materiału objętościowego. Możesz także obliczyć objętość określoną na podstawie gęstości cieczy, jak pokazano w poniższym przykładzie.

Przykład 5: Specyficzna objętość denaturowanego alkoholu

Określ konkretną objętość denaturowanego alkoholu, wiedząc, że ma on gęstość 0,876 g/ml.

• Rozwiązanie: Wiemy, że konkretna objętość jest odwrotnością gęstości, więc:

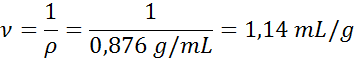
Dla gazów

W związku z faktem, że większość gazów stosunkowo dobrze przestrzega prawa gazów idealnych, to równanie to można wykorzystać do określenia określonej wartości objętości gazu. Po ponownym zorganizowaniu tego równania uzyskuje się następujący związek:

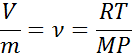
gdzie R, T, M i P są odpowiednio stałą gazów idealnych, temperatury, masy molowej gazu i ciśnienia.

Przykład 6: Specyficzna objętość powietrza

Oblicz specyficzną objętość próbki powietrza znalezionej przy 2 atm ciśnienia i 350 ° C, wiedząc, że średnia masa molowa powietrza wynosi 28,96 g/mol.

• Rozwiązanie: Aby użyć tego równania, konieczne jest przekształcenie temperatury do Kelvina, dodając 273 w temperaturze w stopniach Celsjusza: t = 350+273 = 623 K. Teraz możemy zastosować poprzednie równanie, używając wartości stałej r = 0,08206 ATL.L/mol.K: