Średnia definicja i wzory prędkości kątowej, rozwiązane ćwiczenia

Średnia prędkość kątowa obrotu definiuje się jako kąt obrócony przez pozycję jednostki czasowej wektora punktu, który opisuje ruch kołowy. Ostrza wentylatora sufitowego (takie jak ten pokazany na rycinie 1), podążają za ruchem okrągłym i jego średniej prędkości kątowej obrotu, obliczane są przez stosowanie między kącie skręconym a czasem, w którym przejechano ten kąt.

Zasady, stosowane przez ruch rotacji, są w określony sposób podobne do już krewnych ruchu translacyjnego. Przebyte odległości można również mierzyć w metrach, jednak wielkości kątowe nabierają specjalnego znaczenia, ponieważ znacznie ułatwiają opis ruchu.

Rysunek 1. Ostrza wentylatora mają prędkość kątową. Źródło: Pixabay

Greckie litery są zwykle używane do wielkości kątowych i liter łacińskich dla odpowiednich wielkości liniowych.

[TOC]

Definicja i wzory

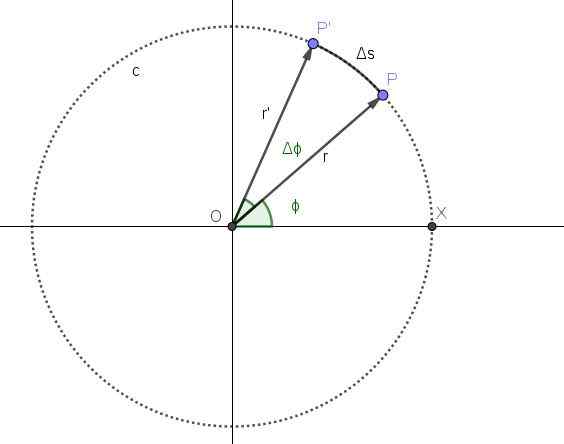
Rycina 2 przedstawia ruch punktu na okrągłej trajektorii C. Pozycja P punktu odpowiada natychmiastowej t i pozycji kątowej odpowiadającej temu momentowi wynosi ϕ. 

Od momentu upływu okresu δt. W tym okresie nowa pozycja punktu wynosi p ', a pozycja kątowa zwiększyła kąt Δϕ.

Rysunek 2. Okrągły ruch punktu. Źródło: Self Made

Średnia prędkość kątowa ω jest kątem przemieszczonym na jednostkę czasu, tak że iloraz psyubli/δt będzie reprezentował średnią prędkość kątową między momentami T i T+δT:

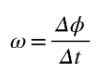
Ponieważ kąt jest mierzony w radianach, a czas w sekundach, jedność średniej prędkości kątowej wynosi rad/s. Jeśli chcesz obliczyć prędkość kątowa Właśnie w czasie t, wówczas iloraz cowy/δt będzie musiał zostać obliczony, gdy δT ➡0.

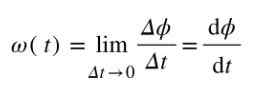Jednostką miary natychmiastowej prędkości kątowej jest również RAD/s.

Może ci służyć: 31 rodzajów siły w fizyce i ich cechy

Jednolity obrót

Ruch obrotowy jest jednolity, jeśli w dowolnym momencie zaobserwowano, przemieszczony kąt jest taki sam w tym samym okresie czasu. Jeśli obrót jest jednolity, wówczas prędkość kątowa w dowolnym momencie pokrywa się ze średnią prędkością kątową.

W jednolitym ruchu obrotowym czas, w którym nazywany jest całkowity zakręt, nazywany jest okres I jest oznaczone t. 

Ponadto, gdy przejechany kąt jest pełny, jest 2π, więc w jednolitym obrocie prędkość kątowa ω jest powiązana z okresem t, według następującego wzoru:

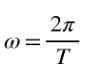
częstotliwość F jednolitego obrotu, takiego jak stosunek między liczbą zakrętów i czasem spędzonym na ich podróżowaniu, to znaczy w czasie czasu δt występuje częstotliwość:

F = n/δt

Jako okrążenie (n = 1) jest podróżowane w czasie t (okres), dostępna jest następująca relacja:

F = 1/t

Oznacza to, że w jednolitym obrocie prędkość kątowa jest związana z częstotliwością poprzez związek:

Ω = 2π ・ f

Zależność między prędkością kątową a prędkością liniową

Prędkość liniowa v, Jest to iloraz między przebywaną odległością a okresem używanym do podróży. Na rycinie 2 przejechana odległość to długość łuku. 

Arc δS jest proporcjonalny do przejechanego kąta 16 i radia R, spełniając następującą relację:

ΔS = r ・ 16

Ilekroć 16 jest mierzone w radianach.

Jeśli podzielimy poprzednie wyrażenie między okresem δt, otrzymamy:

(ΔS/δT) = r ・ (δϕ/δt)

Pierwszym współczynnikiem członka jest prędkość liniowa i iloraz drugiego elementu Średnia prędkość kątowa:

Może ci służyć: Mount Olympus (Mars)

v = r ・ ω

Rozwiązane ćwiczenia

-Ćwiczenie 1

Porady ostrzy wentylatora dachu pokazane na rycinie 1 poruszają się z prędkością 5 m/s, a ostrza mają promień 40 cm.

Z tymi danymi obliczają: i) średnia prędkość kątowa koła, ii) liczba zwojów, które koło podaje w drugim, iii) okres w sekundach.

Rozwiązanie 

i) prędkość liniowa wynosi v = 5 m/s.

Radio to r = 0,40 m.

Z związku między prędkością liniową a prędkością kątową wyczyścimy to drugie:

v = r ・ ω => ω = v/r = (5 m/s)/(0,40 m) = 12,57 rad/s/s

ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 tury / s

iii) t = 1 / f = 1 / (2 tury / s) = 0,5 s na okrążenie.

-Ćwiczenie 2

Spacer z zabawką porusza się po okrągłym torze 2 m. W wieku 0s jego pozycja kątowa wynosi 0 rad, ale po pewnym czasie jego pozycja kątowa jest

φ (t) = 2 ・ t .

Z tymi danymi 

i) Oblicz średnią prędkość kątową w następujących odstępach czasu [0s, 0.5s]; [0.5s, 1.0s]; [1.0, 1.5s] i wreszcie w okresie [0.0, 1.5s]. 

ii) na podstawie wyników części I), co można powiedzieć o ruchu?

iii) Określ średnią prędkość liniową w tym samym okresie odcinka I)

iv) Znajdź prędkość kątową i prędkość liniową dla dowolnego momentu.

Rozwiązanie 

i) Średnia prędkość kątowa podaje następujący wzór:

Kontynuujemy obliczanie przejechanego kąt i upłynął okres czasu w każdym przedziale.

Interwał 1: 16 ϕ (0.5s) - ϕ (0.0s) = 2 (rad/s)*0.5s - 2 (rad/s)*0.0s = 1.0 rad

                   ΔT = 0.5s - 0.0s = 0.5s

Może ci służyć: BTU (jednostka termiczna): równoważniki, zastosowania, przykłady

                   Ω = cowy/δt = 1.0Rad/0.5s = 2.0 rad/s

Interwał 2: 16 ϕ (1.0s) - ϕ (0.5s) = 2 (rad/s)*1.0s - 2 (rad/s)*0.5s = 1.0 rad

                   ΔT = 1.0s - 0.5s = 0.5s

                   Ω = cowy/δt = 1.0Rad/0.5s = 2.0 rad/s

Odstęp 3: 16 ϕ (1.5s) - ϕ (1.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*1.0s = 1.0 rad

                   ΔT = 1.5s - 1.0s = 0.5s

                   Ω = cowy/δt = 1.0Rad/0.5s = 2.0 rad/s

Interwał 4: 16 ϕ (1.5s) - ϕ (0.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*0.0s = 3.0 rad

                   ΔT = 1.5s - 0.0s = 1.5s

                   Ω = cowy/δt = 3.0Rad/1.5s = 2.0 rad/s

ii) Z uwagi na poprzednie wyniki, w których obliczono średnią prędkość kątową w różnych odstępach czasu, ten sam wynik jest zawsze uzyskiwany. Wydaje się, że wskazuje, że jest to jednolity ruch kołowy. Jednak wyniki te nie są rozstrzygające.

Sposób, aby zapewnić wniosek, jest obliczenie średniej prędkości kątowej dla dowolnego przedziału [T, T -T)

                                     ΔT = t ' - t

                                     Ω = cowy/δt = 2*(t'-t)/(t'-t) = 2.0 rad/s

Oznacza to, że spacer zabawkowy ma stałą średnią prędkość kątową 2 rad/s w dowolnym okresie rozważanym. Ale możesz pójść dalej, jeśli obliczana zostanie natychmiastowa prędkość kątowa:

Jest to interpretowane, ponieważ samochód zabawkowy przez cały czas ma stałą prędkość kątową = 2 rad/s.

Bibliografia

1. Giancoli, zm. Fizyka. Zasady z aplikacjami. 6. edycja. Prentice Hall. 30-45.
2. Kirkpatrick, L. 2007. Fizyka: spojrzenie na świat. 6^ta Skrócone wydanie. Cengage Learning. 117.
3. Resnick, r. (1999). Fizyczny. Tom 1. Trzecie wydanie po hiszpańsku. Meksyk. Continental Editorial Company S.DO. c.V. 33-52.
4. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wydanie. Meksyk. Redaktorzy edukacyjni Cengage. 32-55.
5. Wikipedia. Prędkość kątowa. Odzyskane z: Wikipedia.com