Ruch względny w wymiarze, w dwóch wymiarach, ćwiczenia

On Ruch względny cząstki lub obiektu jest obserwowana w odniesieniu do konkretnego punktu odniesienia, który wybrał obserwator, który może być ustalony lub poruszony. Prędkość zawsze odnosi się do niektórych układów współrzędnych używanych do opisania tego.

Na przykład Co -Pilot poruszającego się samochodu, który podróżuje wygodnie śpi na jego siedzeniu, spoczywa w odniesieniu do kierowcy, ale nie jest dla obserwatora stojącego na chodniku, który widzi przejście samochodu.

Rysunek 1. Samoloty utrzymują pewną względną prędkość między nimi podczas ćwiczeń akrobatycznych. Źródło: Pixabay.

Wtedy ruch jest zawsze względny, ale zdarza się, że układ współrzędny lub odniesienia jest zwykle wybierany, mając pochodzenie w ziemi lub ziemi, miejsce uważane. W ten sposób problem koncentruje się na opisie ruchu badanego obiektu.

Czy można opisać prędkość śpiącego kierowcę w odniesieniu do pasażera podróżującego innym samochodem? Odpowiedź brzmi tak. Istnieje swoboda wyboru wartości (x_albo, I_albo, z_albo): Pochodzenie systemu odniesienia. Wybór jest arbitralny i zależy od preferencji obserwatora, a także od łatwości, jaką zapewniasz rozwiązanie problemu.

[TOC]

Ruch względny w wymiarze

Kiedy ruch przechodzi wzdłuż linii prostej, telefony komórkowe mają prędkości w tym samym kierunku lub w przeciwnym kierunku, oba widoczne przez obserwatora stojącego na lądzie (t). Czy obserwator porusza się w sprawie telefonów komórkowych? Tak, z tą samą prędkością, jaką noszą, ale w przeciwnym kierunku.

Jak porusza się mobilny w odniesieniu do drugiego? Aby dowiedzieć się, że prędkości są dodawane wektor.

Może ci służyć: Pluton (Planet Dwarf))

-Rozwiązany przykład 1

W odniesieniu do pokazanego rysunku wskazuj względną prędkość samochodu 1 w odniesieniu do samochodu 2 w każdej sytuacji.

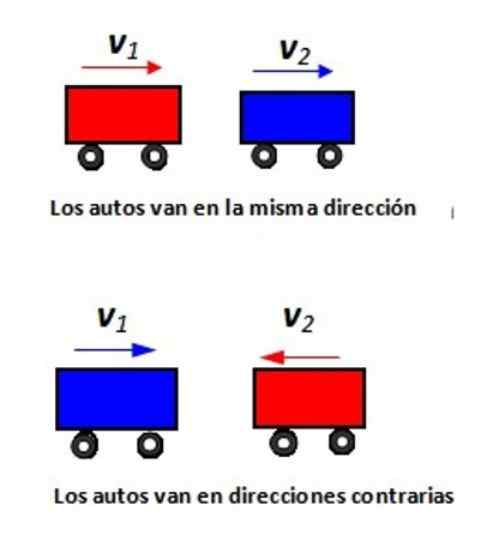Rysunek 2. Dwa samochody idą na prostoliniową drogę: a) w tym samym kierunku i b) w przeciwnych kierunkach.

Rozwiązanie

Przypisamy dodatni znak do prędkości po prawej stronie i znak ujemny po lewej stronie. Jeśli telefon komórkowy pójdzie po prawicy na 80 km/h, pasażer w tym telefonie komórkowym widzi obserwatora na ziemi przemieszczającej się do - 80 km/h.

Załóżmy, że wszystko dzieje się wzdłuż osi x. Na poniższym rysunku czerwony samochód porusza się przy +100 km/h (widoczny z t) i przygotowuje się do przejścia niebieskiego samochodu, który podróżuje przy +80 km/h (również widoczne z t). Z jaką prędkością widzisz pasażera zbliżającego się do czerwonego samochodu w niebieskim samochodzie?

Etykiety to: v _1/2 Auto 1 prędkość w odniesieniu do 2, v_1/t prędkość samochodu w odniesieniu do t, v_T/2 Prędkość stołowa w odniesieniu do 2. Dodawanie wektorowe:

v_1/2 = v_1/t + v_T/2 = (+100 km/h - 80 km/h) X= 20 km/h X

Możemy się obejść bez notacji wektorowej. Zwróć uwagę na indeksy: pomnożenie obu po prawej stronie musi uzyskać ten po lewej stronie.

A kiedy są w przeciwnym kierunku? Teraz v_1/t = + 80 km/h i v_2/t = -100 km/h, a zatem v_T/2 = + 100 km/h. Pasażer auto niebieskiego zobaczy zbliżający się czerwony samochód:

v_{1/2 =} v_1/t + v_T/2 = +80 km/h +100 km/h = 180 km/h

Ruch względny w dwóch i trzech wymiarach

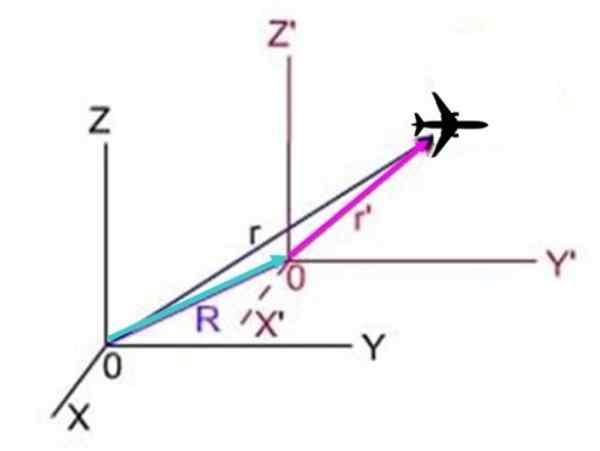
W następnym schemacie, R Jest to pozycja płaszczyzny widocznej z systemu X i Z, R„Jest to pozycja z systemu X i Z ' I R Jest to pozycja systemu z premią w odniesieniu do systemu bez premii. Trzy wektory tworzą trójkąt, w którym R + R'= R, W związku z tym R'= r - r.

Rysunek 3.- Płaszczyzna porusza się w odniesieniu do dwóch układów współrzędnych, z kolei jeden z układów porusza się w odniesieniu do drugiego.

Ponieważ pochodna w odniesieniu do czasu pozycji jest właśnie prędkość, wyniki:

Może ci służyć: strzał paraboliczny: cechy, wzory i równania, przykłady

v'= v - Lub

W tym równaniu v„Jest to prędkość płaszczyzny w odniesieniu do systemu X i Z ', v to prędkość w odniesieniu do systemu X i Z I Lub Jest to stała prędkość systemu podstawowego w odniesieniu do systemu bez składek.

-Ćwiczenie rozwiązane 2 

Samolot znajduje się w kierunku północnym z prędkością w odniesieniu do powietrza 240 km/h. Nagle zaczyna dmuchać wiatr z zachodu na wschód z prędkością 120 km/ zgodnie z ziemią.

Znajdź: a) prędkość płaszczyzny w odniesieniu do ziemi, b) odchylenie doświadczane przez pilota C) korekta, którą pilot musi dokonać, aby móc wskazać bezpośrednio na północ, i nową prędkość w odniesieniu do ziemi, raz Korekta została dokonana.

Rozwiązanie

a) Miał następujące elementy: płaszczyzna (a), ziemia (t) i wiatr (v).

W układzie współrzędnych, w którym północ jest + i kierunek zachodni-wschód + X istnieją podane prędkości i ich odpowiednia etykieta (indeksypty):

v _Av = 240 km/h (+I); v _V/t = 120 km/h (+X); v _Na = ?

Odpowiednia suma wektora to:

v _Na = v _Av + v _V/t = 240 km/h (+I) + 120 km/h (+X)

Wielkość tego wektora to: v _Na = (240 ²+ 120²)^1/2 km/h = 268.3 km/h

b) θ = arctg (v _Av / v _V/t) = ARCTG (240 /120) = 63.4. na północ od wschodu lub 26.6. północny wschód.

c) Aby kontynuować na północ z tym wiatrem, musisz wskazać łuk samolotu na północny zachód, aby wiatr popychał go bezpośrednio na północ. W tym przypadku prędkość płaszczyzny widoczna z ziemi będzie w +i, chociaż prędkość płaszczyzny w odniesieniu do wiatru będzie na północny zachód (niekoniecznie wynosi 26.6).

Może ci służyć: Twierdzenie Bernoulli

Autor: PiThagoras Twierdzenie:

v _Na = (240 ²- 120²)^1/2 km/h = 207.8 km/h

α = arctg (v _V/t / v _Na ) = ARCTG (120/207.8) = 30. na północny zachód

-Ćwiczenie rozwiązane 3

Osoba zajmuje 2 minuty, aby spacerować po nieruchomych mechanicznych schodach. Jeśli schody działają, osoba zajmuje 1 minutę, aby zejść na dół. Jak długo dana osoba zajmuje chodzenie i bieganie schodów?

Rozwiązanie

Należy wziąć pod uwagę trzy elementy: osoba (P), schody (E) i ziemia, których względne prędkości to:

v_P/E : szybkość osoby w odniesieniu do drabiny; v_JEST: prędkość schodów w odniesieniu do ziemi; v_P/s: Prędkość osoby w odniesieniu do ziemi.

Jak widać z ziemi przez ustalonego obserwatora, osoba, która obniża schody (e), ma prędkość v _P/s podane przez:

v _P/s = v_P/E + v_JEST

Pozytywny zmysł spada po schodach. Być T  czas potrzebny na chodzenie i L dystans. Wielkość osoby v _P/s Jest:

v_P/s = L / t

T₁ To czas, aby przejść na spacer z zatrzymaną drabiną: v _P/E = L / t₁

Oraz T₂ Ten, który zaciąga cię wciąż na schodach w ruchu: v _JEST = L / t₂

Łączenie wyrażeń:

L / t = l / t₁ + L / t₂

Zastępowanie wartości numerycznych i rozliczenie T:

1 / t = 1 / t₁ + 1 / t₂ = 1/2 + 1/1 = 1.5

Następnie t = 1/1.5 minut = 40 sekund.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 84-88.
2. Figueroa, zm. Seria fizyczna dla nauki i inżynierii. Tom 3. Wydanie. Kinematyka. 199-232.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6^th. Wyd. Prentice Hall. 62-64.
4. Ruch względny. Odzyskane z: kursów.Lumenarning.com
5. Wilson, J. 2011. Fizyka 10. Edukacja Pearsona. 166-168.