Jakie są wektory koplanares? (Z rozwiązanymi ćwiczeniami)

Wektory koplanares o coplanarios to osoby zawarte na tej samej płaszczyźnie. Kiedy masz tylko dwa wektory, są one zawsze kupletowe.

Jeśli masz trzy lub więcej wektorów, być może żaden z nich nie jest w tej samej płaszczyźnie co inne, dlatego nie można ich uznać. Poniższy rysunek pokazuje zestaw koplanares oznaczonych w odważnych wektorach DO, B, C I D:

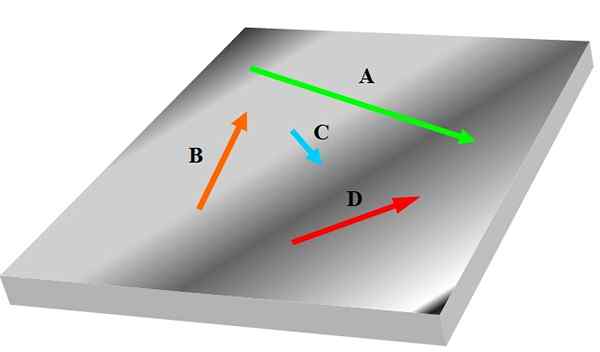Rysunek 1. Cztery koplanares. Źródło: Self Made.

Wektory są związane z zachowaniem i właściwościami odpowiednich wielkości fizycznych w nauce i inżynierii; na przykład prędkość, przyspieszenie i siła.

Siła wytwarza różne skutki na obiekt, gdy sposób, w jaki jest stosowany, jest zróżnicowany, na przykład zmieniający intensywność, kierunek i znaczenie. Wciąż zmieniając jeden z tych parametrów, wyniki są znacznie różne.

W wielu aplikacjach, zarówno pod względem statycznym, jak i dynamiki, siły działające na ciele są na tej samej płaszczyźnie, dlatego są uważane za koplanares.

[TOC]

Warunki dla wektorów, które były koplanaresami

Aby trzy wektory były coplanares, muszą być na tej samej płaszczyźnie i dzieje się tak, jeśli spełniają którekolwiek z następujących warunków:

-Wektory są równoległe, dlatego ich składniki są proporcjonalne i są zależne od liniu.

-Twój mieszany produkt jest nieważny.

-Jeśli masz trzy wektory i którekolwiek z nich można zapisać jako liniową kombinację pozostałych dwóch, wektory te są koplanares. Na przykład wektor, który wynika z suma dwóch innych, wszystkie trzy są w tej samej płaszczyźnie.

Może ci służyć: woltometr: Charakterystyka, operacja, do czego jest typów

Alternatywnie warunek kopalanarności można ustalić w następujący sposób:

U v w Są to koplanares, jeśli istnieją trzy liczby (skalarne) α, β, γ, tak że αLub + βv + γW = 0 Z (α, β, γ) różni się od (0, 0, 0)

Mieszany produkt między trzema wektorami

Mieszany produkt między wektorami jest zdefiniowany z trzema wektorami Lub, v I W, powodując skalar, który wynika z wykonania następującej operacji:

Lub · (v X W) = Lub · (v X W)

Najpierw powstaje produkt krzyżowy w nawiasach: v X W, którego wynik jest normalnym (prostopadłym) wektorem do płaszczyzny, w której tak są v Jak W.

Tak Lub jest na tej samej płaszczyźnie co v I W, Oczywiście produkt skalarny (produkt punktowy) między U i wspomnianym wektorem normalny musi wynosić 0. W ten sposób weryfikuje się, że trzy wektory to koplanares (leżą na tej samej płaszczyźnie).

Gdy produkt mieszany nie jest zerowy, jego wynik jest równy objętościom równoległości, który ma wektory Lub, v I W jako sąsiednie strony.

Aplikacje

Coplanares, równoległe i niekolinealne siły

Mocne strony równoległy Wszystkie są stosowane w tym samym punkcie. Jeśli są również koplanaresami, można je zastąpić tylko jednym, który się nazywa wynikowa siła I ma taki sam efekt jak na oryginalnych sił.

Jeśli ciało jest w równowadze dzięki trzem koplanaresom, zwolennik DO, B I C, On Twierdzenie Lamy Wskazuje, że związek między tymi siłami (wielkości) jest następujący:

A / sin α = b / sen β = c / sen γ

Z α, β i γ jako kąty przeciwne stosowanym siłom, jak pokazano na poniższym rysunku:

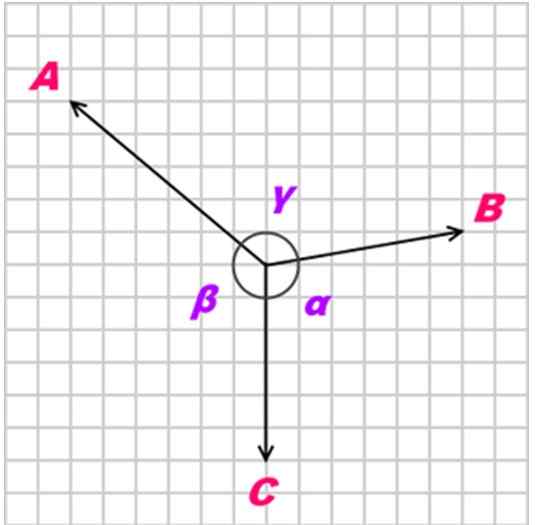Rysunek 2. Trzy siły A, B i C Coplanares działają na obiekcie. Źródło: Kiwakwok w angielskiej Wikipedii [domena publiczna]

Rozwiązane ćwiczenia

-Ćwiczenie 1

Znajdź wartość K, aby następujące wektory to koplanares:

Może ci służyć: Carnot Machine

Lub =

v =

W =

Rozwiązanie

Ponieważ składniki wektorów są używane, stosuje się kryteria produktu mieszanego, dlatego:

Lub · (v X W) = 0

Jest to najpierw rozwiązane v X W. Wektory zostaną wyrażone w kategoriach wektorów jednostkowych Siema, J I k które rozróżniają trzy prostopadłe kierunki w przestrzeni (szeroka, wysoka i głębokość):

v= 4 Siema + J + 0 k

W= -1 Siema + 2J -1 k

v X W = -4 (i x i) + 8 (i x j) - 4 (i x k) - (J x i) + 2 (J x j) - 2 (J x k) = 8 k + 4 J + k -2 i = -2 Siema + 4 J + 9 k

Produkt skalarny jest teraz proponowany między U a wektorem, który ma wyniki z poprzedniej operacji, dopasowując operację do 0:

Lub · (v X W) = (-3 Siema + k J + 2 k) · (-2 Siema + 4 J + 9 k) = 6 + 4k +18 = 0

24 + 4k = 0

Poszukiwana wartość to: k = - 6

Tak, aby wektor Lub Jest:

Lub =

-Ćwiczenia 2

Rysunek pokazuje obiekt, którego waga wynosi w = 600 n, wisząc w równowadze dzięki kablom umieszczonym zgodnie z kątami pokazanymi na rycinie 3. Czy można zastosować twierdzenie Lamy w tej sytuacji? W każdym razie znajdź wielkości T₁, T₂ I T₃ które umożliwiają równowagę.

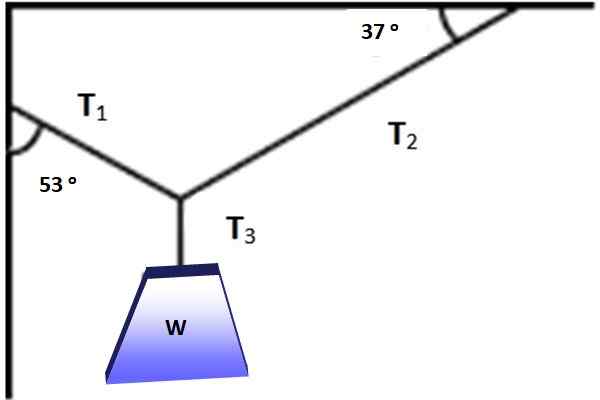Rysunek 3. Waga wisi w równowadze pod działaniem trzech pokazanych napięć. Źródło: Self Made.

Rozwiązanie

Twierdzenie Lamy ma zastosowanie w tej sytuacji, jeżeli węzeł, na którym stosuje się trzy napięcia. Najpierw wykonany jest schemat wolnego ciała dla wiszącego masy, aby określić wielkość t_3:

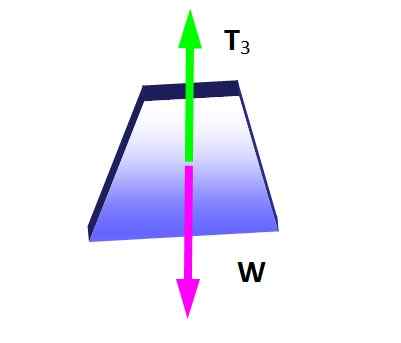Rysunek 4. Darmowy schemat ciała do wiszącego ciężaru. Źródło: Self Made.

Z warunków równowagi następuje:

Może ci służyć: dyfrakcja dźwięku: co to jest, przykłady, aplikacje

T₃  = W = 600 n

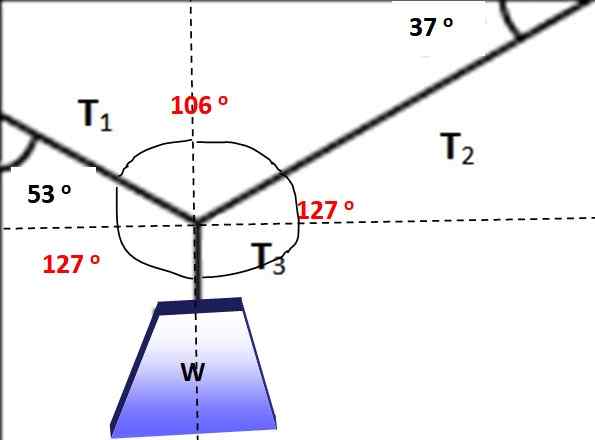
Kąty między siłami są oznaczone na czerwono na poniższym rysunku, można łatwo zweryfikować, że jego suma wynosi 360 °. Teraz można zastosować twierdzenie Lamy, ponieważ jedna z sił i trzy kąty między nimi jest znane:

Rysunek 5.- Na czerwono kątów, aby zastosować twierdzenie Lamy. Źródło: Self Made.

T₁ / Sen 127º = w / sen 106º

Dlatego: t₁ = Sen 127º (w /Sen 106º) = 498.5 n

Znowu twierdzenie Lamy jest stosowane w celu wyczyszczenia t₂:

T₂ / sin 127 = t₁ / Sen 127º

T₂ = T₁ = 498.5 n

Bibliografia

1. Figueroa, zm. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. 31-68.
2. Fizyczny. Moduł 8: wektory. Odzyskane z: frtl.Utn.Edu.ar
3. Hibbeler, R. 2006. Mechanika inżynierów. Statyczny. 6. edycja. Continental Editorial Company.28-66.
4. McLean, w. Seria Schaum. Mechanika inżynierów: statyczne i dynamiczne. Wydanie trzecie. McGraw Hill. 1-15.
5. Wikipedia. Wektor. Odzyskane: to jest.Wikipedia.org.