Wartość względna

Jaka jest względna wartość liczby?

On Wartość względna liczby o Digit systemu dziesiętnego zależy od pozycji, w której zajmuje to, gdy jest częścią figury. Dlatego mówi się, że jest to wartość pozycyjna. Bardzo prosty przykład: The Wartość względna 1 W numerze 123, Będzie 100, Ponieważ 1 zajmuje pozycję setek.

Inny przykład: Liczba 58 jest tworzona za pomocą cyfr 5 i 8. Badając tę ​​liczbę od prawej do lewej, względna wartość 8 wynosi 8, ponieważ jest w pozycji jednostek, a wartość względna 5 wynosi 50, do zajęcia miejsca dziesiątek. Liczba jest odczytywana „Pięćdziesiąt lat”.

Z drugiej strony te same cyfry mają różne wartości względne w numerze 85, ponieważ wymieniły pozycje. Zawsze zaczynając od prawej do lewej, względna wartość 5 w tym przypadku wynosi 5, wartość względna 8 to 80, a liczba jest odczytywana „osiemdziesiąt pięć”.

Jak znaleźć względną wartość liczby?

Ogólna procedura znalezienia wartości względnej każdej cyfry jest następująca:

• Pierwsza cyfra od prawej do lewej znajduje się w pozycji jednostek, a ich wartość jest mnożona przez 1.
• Poniższa cyfra odpowiada dziesiątkom i jest mnożona przez 10.
• Następna pozycja odpowiada setkom, a wartość cyfry jest mnożona przez 100.
• Następna pozycja to tysiąc, dlatego cyfra jest mnożona przez 1000.

I tak dalej dla większych liczb, mnożąc cyfrę przez odpowiednią 10 mocy: 100000, 100000 i nie tylko.

Na przykład liczba 321 można zapisać jako 3*100 + 2*10 + 1*1 lub równoważny 300 + 20 + 1. W poprzednim przykładzie można szybko zauważyć, że względna wartość 3 wynosi 300, 2 to 20, a 1 to 1.

Może ci służyć: nieruchomość dystrybucyjna

Przykłady wartości względnych

Numer 727

Aby określić względną wartość cyfry, musisz kierować się następującą podstawową zasadą pisemnej numeracji systemu dziesiętnego:

Dowolna cyfra po lewej stronie reprezentuje jednostkę 10 razy wyższą i odwrotnie: każda cyfra po prawej stronie, reprezentuje jednostkę 10 razy mniejszą. 

Na przykład liczba 727, która brzmi „siedemset dwadzieścia siedem”, składa się z cyfr 2 i 7, z 7 powtarzanymi, ale zajmującymi różne pozycje.

Czytając 727 od prawej do lewej, obserwuje się, że 7 po prawej zajmuje pozycję urządzenia, dlatego jest on mnożony przez 1:

7 x 1 = 7

A jego względna wartość wynosi 7.

Digit 2 pośrodku zajmuje pozycję dziesiątek i aby znaleźć ich względną wartość, jest ona mnożona przez 10:

2 x 10 = 20

Wreszcie po 7 do skrajnej lewicy ma pozycję setek. Następnie musisz pomnożyć przez 100, a jego względna wartość to:

7 x 100 = 700

Zauważ, że tylko wtedy, gdy cyfra zajmuje pozycję jednostki, polega na tym, że jej wartość bezwzględna i wartość względna są równe. Dlatego jeśli wartością względną liczby jest VR, a jej wartością bezwzględną jest VA, ogólną formułą do znalezienia wartości względnej jest:

VR = wartość bezwzględna VA × Wartość jej pozycji

Figurę można zapisać jako sumę względnych wartości cyfr, jest to znane jako rozwinięta notacja. Kontynuując przykład numeru 727, musisz:

727 = 700 + 20 + 7

A jeśli wolisz używać mocy 10, liczba 727 jest również wyrażona równoważna jako:

727 = 7 ∙ 10² + 2 ∙ 10¹ + 7 ∙ 10⁰

Może ci służyć: wielokrotności 8: co to jest i wyjaśnienie

Gdzie wykładniki mocy oparte na 10 reprezentują pozycję każdej cyfry i są wywoływane Wskaźniki. Na poniższym rysunku zilustrowano inny przykład.

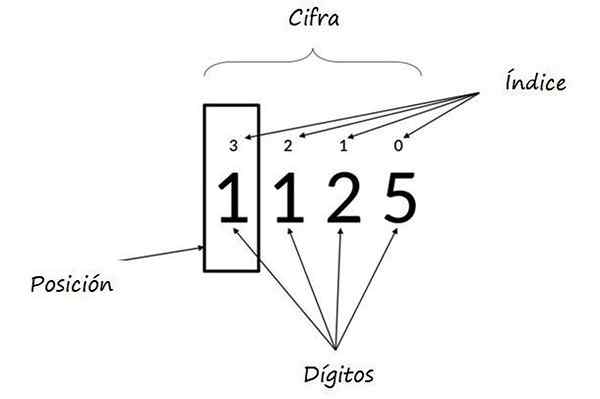W numerze 1125, względna wartość 5 wynosi 5, 2 to 20, 1 to 100, a po lewej 1 w pudełku wynosi 1000. Źródło: Wikimedia Commons.

Numer 63

Zaczynając od lewej do prawej, 3 jest w pozycji jednostek, dlatego:

Wartość względna 3: 3 x 1 = 3

Jeśli chodzi o 6, jest to w pozycji dziesiątki, zatem:

Wartość względna 6: 6 x 10 = 60

Numer 603

Ta liczba różni się od poprzedniej, ponieważ chociaż wartość względna 0 to 0, pozostałe cyfry mają różne wartości względne. Zaczynając od prawej do lewej jak zawsze:

• Wartość względna 3: 3 x 1 = 3
• Wartość względna 0: 0 x 10 = 0
• Wartość względna 6: 6 x 100 = 600

Numer 630

W takim przypadku 0 jest w pozycji jednostek:

• Wartość względna 0: 0 x 1 = 0
• Wartość względna 3: 3 x 10 = 30
• Wartość względna 6: 6 x 100 = 600

Rozwiązane ćwiczenia

Ćwiczenie 1

Wskaż względną wartość podkreślonych liczb:

a) 1209

b) 2782

c) 376

d) 3045

e) 273

Rozwiązanie

a) cyfra 1 w 1209 r. Zajmuje pozycję tysięcy lub tysięcy. Dlatego jego względna wartość wynosi 1000.

VR (1) = 1 x 1000 = 1000

b) 2 zajmuje pozycję jednostek w 2782 r., Dlatego jego względna wartość wynosi 2.

c) W 376 7 znajduje się w pozycji dziesiątek i:

VR (7) = 7 x 10 = 70.

d) W 3045 4 znajduje się również w pozycji dziesiątek:

VR (4) = 4 x 10 = 40.

e) do 273 3 znajduje się na miejscu jednostek, a ich względna wartość pokrywa się z figurą cyfry, to znaczy:

Może ci służyć: sześciokątna piramida

VR (3) = 3 x 1 = 3

Ćwiczenie 2

Napisz najniższą liczbę 5 cyfr, bez żadnych powtarzanych i spełniaj następujące warunki:

a) że wszystkie cyfry są różne

b) Ma 7 w tysiącach

c) 8 znajduje się w pozycji jednostek.

Rozwiązanie

Najmniejsza liczba 5 -digita, wraz ze wszystkimi z nich, musi rozpocząć się od 1, ponieważ chociaż 0 jest niższa, ponieważ pierwsza cyfra po lewej nie liczy się, dlatego poszukiwana liczba to:

10234

Rozwiązanie b

Pozycja Millar dla 7 odpowiada 7000, ale ponieważ chcesz najmniejszej możliwej liczby zawierającej 5 cyfr, liczba musi rozpocząć się od 1, a następnie 7, a następnie 023 w pozostałych pozycjach, ponieważ nie należy powtórzyć cyfry.

Dlatego liczba to:

17023

Rozwiązanie c

Zgodnie z żądaniem, aby 8 było w pozycji jednostek, musi to być skrajnie prawicy. Będąc najmniej możliwą liczbą, bez powtarzania 5 cyfr, poszukiwana liczba to:

10238

Ćwiczenie 3

Oblicz wartość bezwzględną i względną (każdego rysunku) liczby 579.

Rozwiązanie

Ma, że ​​579 jest równe 5 × 100+7 × 10+9 × 1 lub równoważne, jest równe 500+70+9. Dlatego względna wartość 5 wynosi 500, wartość względna 7 wynosi 70, a 9 to 9.

Z drugiej strony wartość bezwzględna 579 wynosi 579.

Ćwiczenie 4

Podaj numer 9.648.736, jaka jest względna wartość 9 i pierwsza 6 (od lewej do prawej)? Jaka jest wartość bezwzględna danej liczby?

Rozwiązanie

Przepisując na numer 9.648.736 Uzyskuje się, że jest to równoważne

9 × 1.000.000 + 6 × 100.000 + 4 × 10.000 + 8 × 1.000 + 7 × 100 + 3 × 10 + 6 × 1

Lub możesz pisać jak

9.000.000 + 600.000 + 40.000 + 8.000 + 700 + 30 + 6.

Tak że wartość względna 9 wynosi 9.000.000 i względna wartość pierwszej 6 to 600.000.

Z drugiej strony wartość bezwzględna podanej liczby wynosi 9.648.736.